R树详解

$B$ 树的搜索本质上是一维区间的划分过程，每次搜索节点所找到的子节点其实就是一个子区间。$R$ 树是把 $B$ 树的思想扩展到了多维空间，

采用了 $B$ 树分割空间的思想，是一棵用来存储高维数据的平衡树。

          

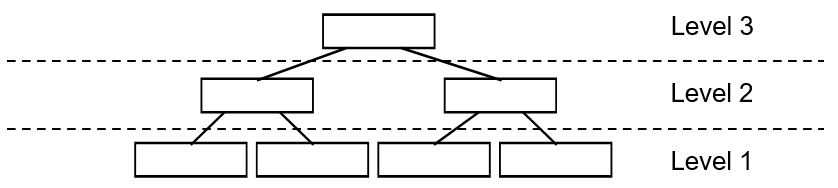
对于一棵 $R$ 树，叶子节点所在层次称为 $Level \; 1$，根节点所在层次称为 $Level \; h$。一棵 $R$ 树满足如下性质：

    1）除根结点之外，所有非根结点包含有 $m$ 至 $M$ 个记录索引（条目）。根结点的记录个数可以少于 $m$。通常 $m=\frac{M}{2}$。

    2）每一个非叶子结点的分支数和该节点内的条目数相同，一个条目对应一个分支。所有叶子结点都位于同一层，因此 $R$ 树为平衡树。

    3）叶子结点的每一个条目表示一个点。

    4）非叶结点的每一个条目存放的数据结构为：$(I, child-pointer)$。$child-pointer$ 是指向该条目对应孩子结点的指针。$I$ 表示

       一个 $n$ 维空间中的最小边界矩形($minimum \; bounding \; rectangle$，即 $MBR$)，$I$ 覆盖了该条目对应子树中所有的矩形或点。

          

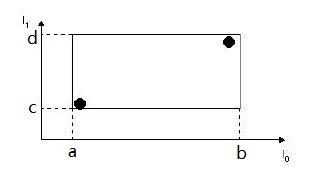
       两个黑点保存在一个叶子节点的两个条目中，恰好框住这两个条目的矩形表示为：$I=(I_0,I_1)$。其中 $I_0=(a,b),I_1=(c,d)$，也就

       是说最小边界矩形是用各个维度的边来表示，在三维空间中那就是立方体，用 $3$ 条边就可以表示了。

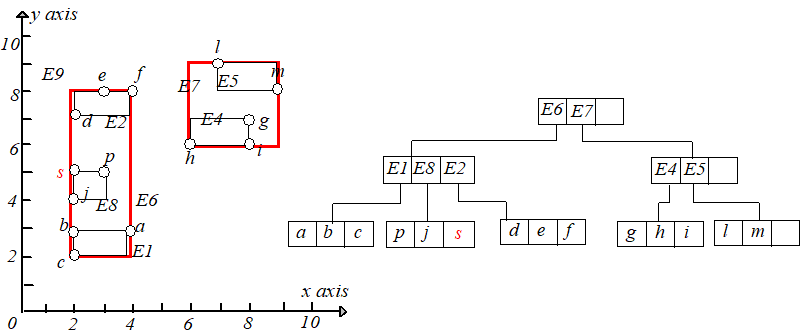
下面构建一棵 $R$ 树。如下左图，理论上，点可以任意组合成叶节点，只要 $MBR$ 包含它子树中的所有点。特别是 $MBR$ 可以重叠。下面

右图是另一种组合建立的 $R$ 树。

    

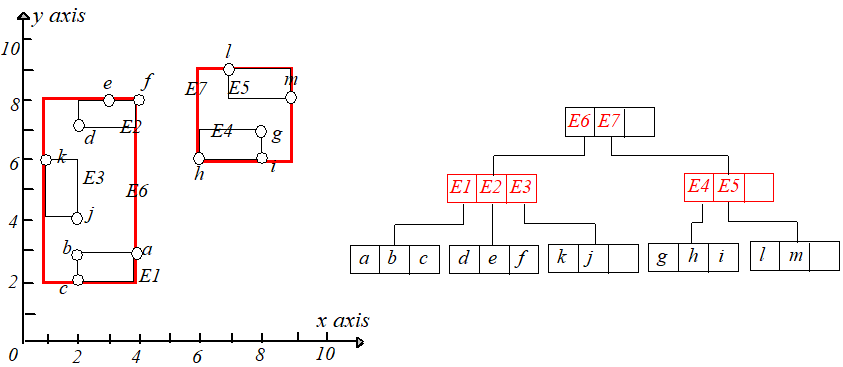
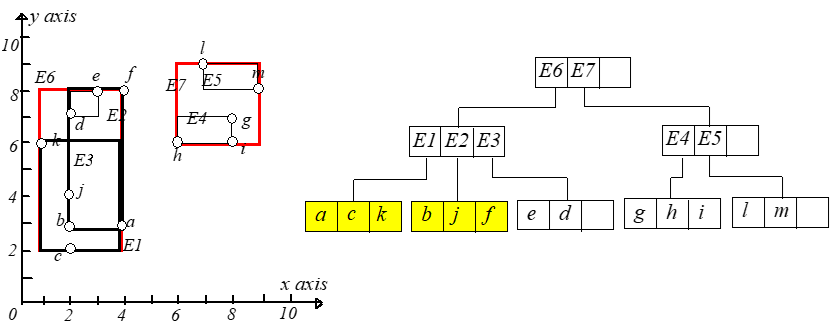
哪种分组更好呢？一般分组的原则就是最小化每个 $MBR$ 矩形，这样查询的时候发生的相交情况会越少，查询的分支就越少，查询效率越高。

 

R-tree 查询

介绍查询之前，需要先了解下：如何判断两个线段或者两个矩形是否相交？

    

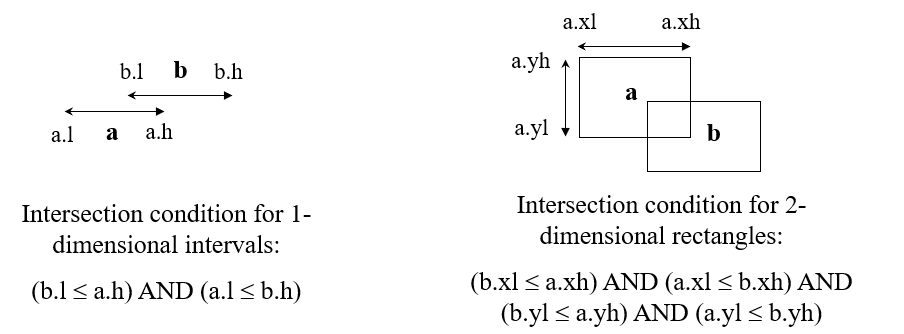
1. Range Query

   这种查询输入的是一个矩形所表示的范围，要求输出该范围内的所有点。从根节点开始，通过判断目标矩形和节点内的每一个条目对应的

   矩形是否相交来选择下一步查询的节点，如果有多个条目都相交，那对应的各个分支都得查。到达叶子节点后，就判断该叶子节点的每一

   个条目是否在查询区域内即可。

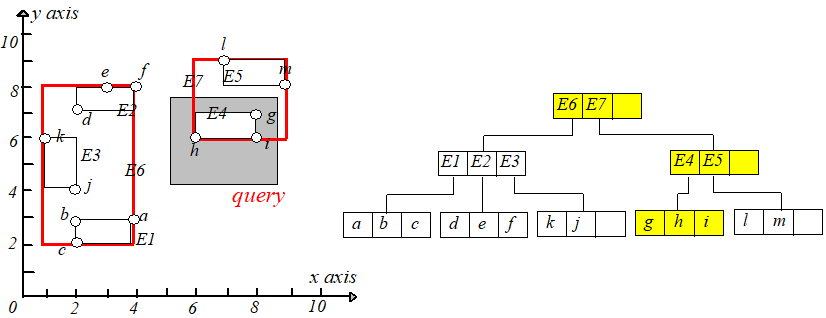
   现在想查询在矩形 $[5,8.5],[4,7.5]$ 内的所有点，即下图中的阴影矩形，设该矩形为 $q$。首先判断 $E6.I,E7.I$ 和 $q$ 是否相交，发现 $E7.I$

   与 $q$ 相交，于是通过 $E7$ 中的 $child-pointer$ 指针到达孩子节点，再判断 $E4.I,E5.I$ 和 $q$ 是否相交，发现 $E4.I$ 与 $q$ 相交，接下来

   就到达叶子节点了，然后判断每个点是否在矩形 $q$ 内即可，如果在则输出。

   

2. Nearest Neighbor Query 

   这种查询输入的是一个点，要求输出离这个点最近的 $k$ 个点，所以又叫 $k-NN$ 查询。首先需要知道如何定义一个点到一个矩形的最

   短距离，记点 $q$ 到矩形 $E$ 的最短距离为 $mindist(q,E)$。规定：以 $q$ 为圆心，与 $E$ 有交点的最小圆的半径就是 $mindist(q,E)$。 

   $k-NN$ 查询有两种算法，下面一一介绍。

   1）Depth-First NN Algorithm

      假设 $k=1$，即查找距 $q$ 最近的一个点。

      输入一个点 $q$，从根节点开始，计算 $q$ 到每个条目对应矩形的最短距离，即 $mindist(q,E6.I),mindist(q,E7.I)$，计算完后从小到大排序。

      因为 $mindist(q,E6.I) < mindist(q,E7.I)$，所以来到 $E6$ 的孩子节点，同样计算 $mindist(q,E1.I),mindist(q,E2.I),mindist(q,E3.I)$，

      并从小到大排序，如下右图。

           

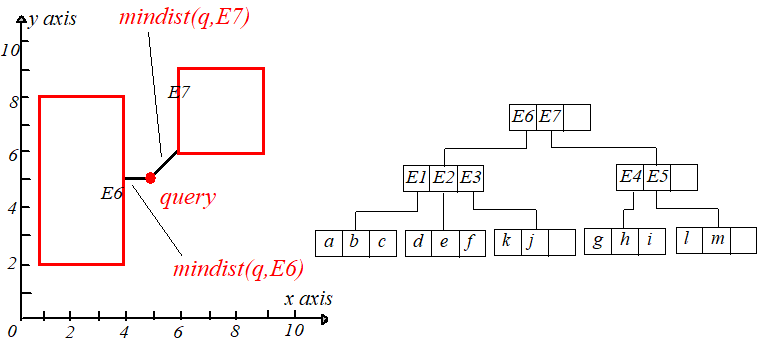
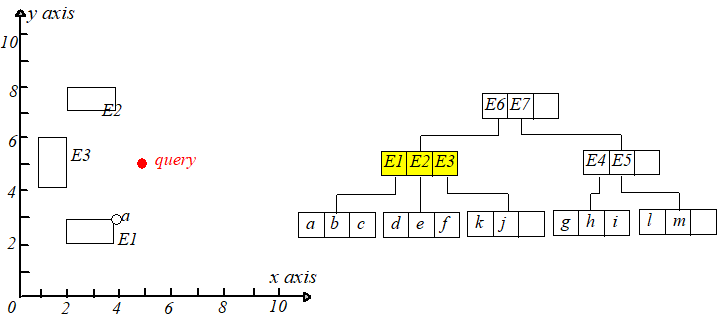
      $q$ 到 $E1.I$ 和 $E2.I$ 有相同的最短距离，于是随机选择一个，这里选择 $E1$，于是来到 $E1$ 的叶子节点。计算点 $a,b,c$ 到 $q$ 点的距离，

      保存距离 $q$ 最近的那个点的距离，显然 $a,q$ 距离最近，这个距离记为 $r$，这个 $r$ 只是当前搜索结果。接下进行回溯，回到上一个节点，注意

      $q$ 到所经过节点每个条目的最短距离都已经算好并升序排列，现在选择距离 $q$ 第二近的那个条目即 $E2$，此时有一步很重要的剪枝操作，需要

      判断$mindist(q,E2.I)$ 和 $r$ 的大小，如果 $mindist(q,E2.I) > r$，那显然没有必要再去搜索它的子树了，因为$E2$ 区域中的点到 $q$ 的距离不

      可能会比 $r$ 小了。

      接下来回溯到根节点，因为 $mindist(q,E7.I) < r$，所以在 $E7$ 区域中可能存在到 $q$ 的距离比 $r$ 小的点，需要搜索。来到 $7$ 的孩子节点，

      计算 $mindist(q,E4.I),mindist(q,E5.I)$ 并升序排列，接下来访问 $E4$ 的孩子节点，发现 $q,h$，的距离小于 $r$，于是用新的最短距离更新 $r$。

          

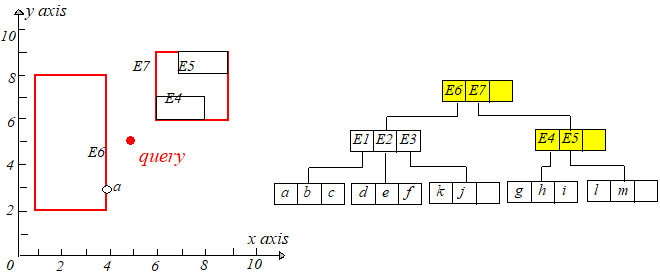
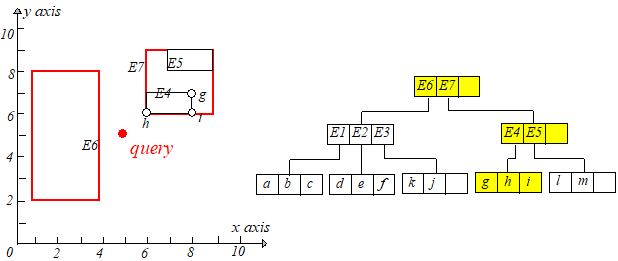
      然后再回溯，在已升序排列的数组里取下一个节点，判断是否剪枝。。。。

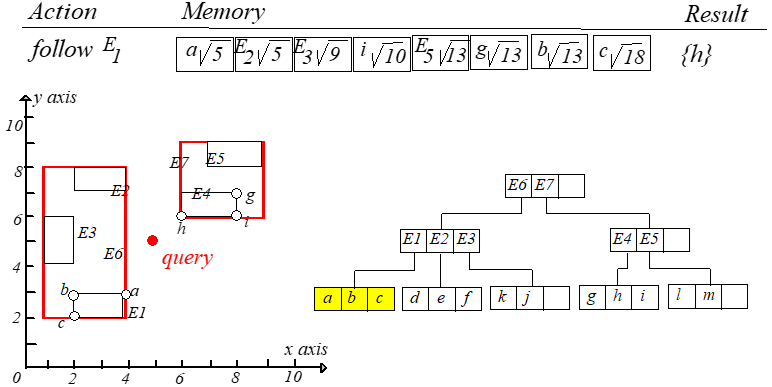
      当 $k=2$ 时，过程也是一样的，只不过要保存两个距离(最短和次短)，并使用次短距离进行剪枝。过程如下：

      a. Root => child node of E6 => child node of E1 => find {a, b} here

            b.   Backtrack to child node of E6 => child node of E2 (its mindist < dist(q, b)) => update the result to {a, f}

            c.   Backtrack to child node of E6 => child node of E3 => backtrack to the root => child node of E7 => child node of E4 => update the result to {a, h}

            d.   Backtrack to child node of E7 => prune E5 => backtrack to the root => end.

              

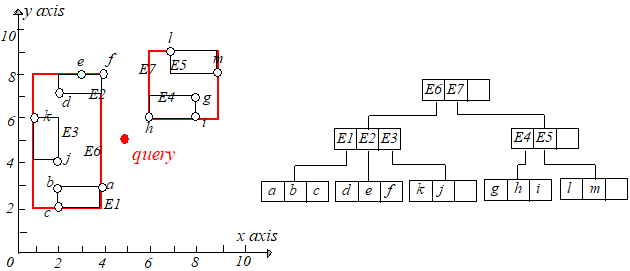
   2）Best-First Algorithm

      这个算法需要维护一张点 $q$ 到所访问条目的最短距离表，这张表按升序排列，直接来看一下搜索过程。

      访问根节点的时候计算 $mindist(q,E6.I),mindist(q,E7.I)$，分别保存为位置 $0$ 和 $1$。每一次迭代都访问第一个元素。计算 $q$ 

      到新结点每个条目的最短距离，然后更新表并重新排序。整个过程如下图所示，从左往右，从上到下阅读。

         

                 

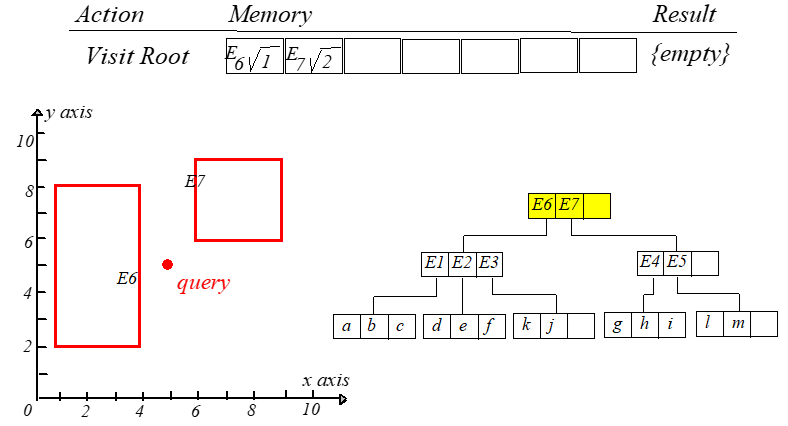
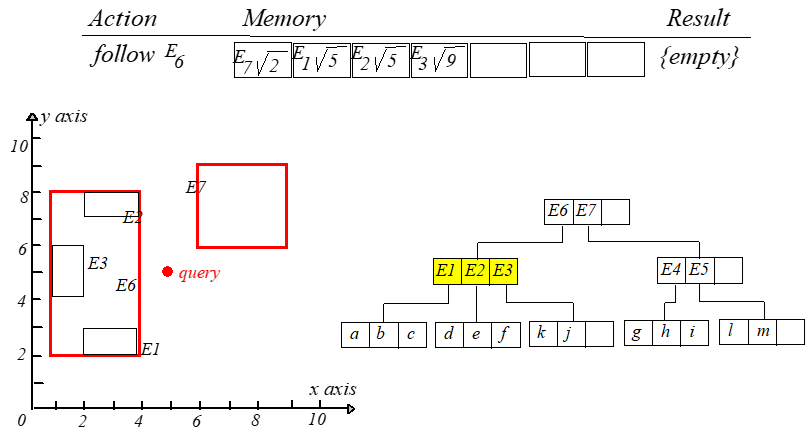
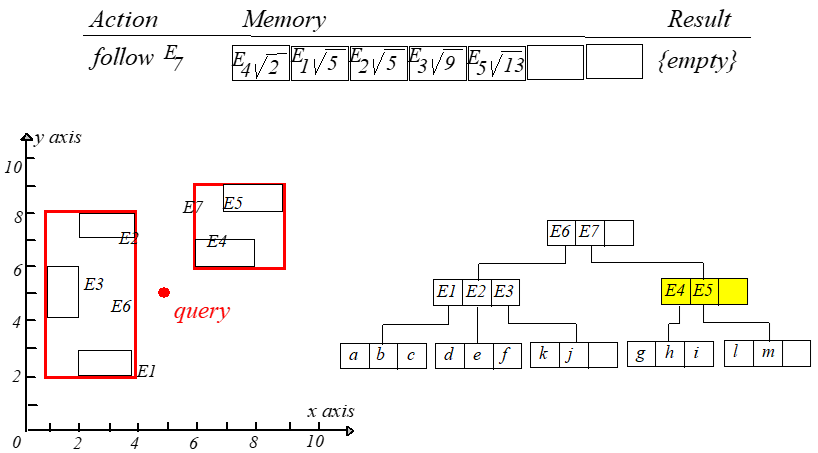
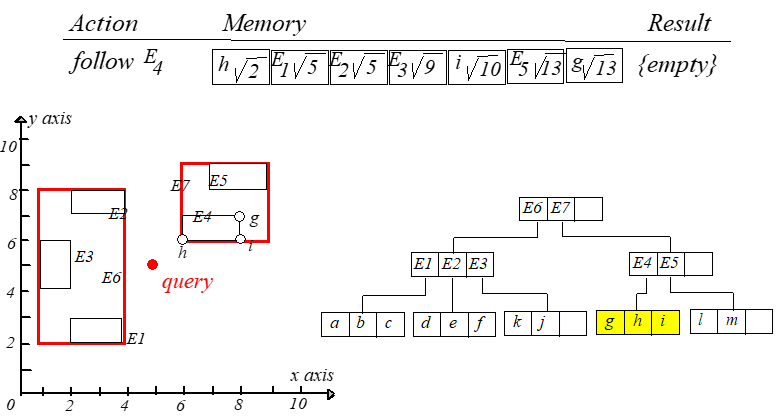
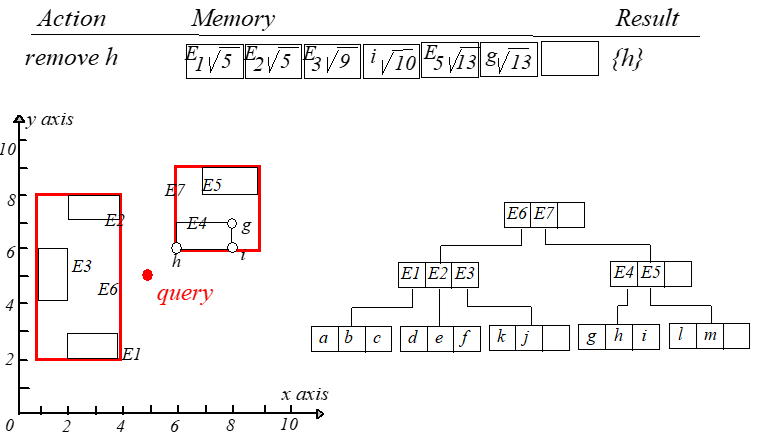
      此时就可以得到点 $h$ 到 $q$ 的距离最短。如果 $k=2$，则继续搜索。   

             

 

R-tree 插入

插入的可以是一个点，也可以说是一个 $R$ 树。

1. 插入一个点 $p$

   设根节点为 $N$，遍历 $N$ 中所有条目，找出添加该点后 $E.I$ 扩张最小的条目(代价最小)，并把该条目对应的孩子节点定义为 $F$。如果有多

   个这样的条目，那么选择面积最小的条目。将 $N$ 设为 $F$，开始上述重复操作直到找到一个叶子节点。

   如果选择出来的叶子节点有足够的空间来放置点 $p$，则直接添加一个条目就可以了。如果没有足够的空间，即插入后该叶子节点含有的条目高

   于 $M$，则需要进行节点分裂。分裂方法如下：

   将插入 $p$ 后的叶子节点分裂为两个结点 $L$ 与 $LL$，这两个结点包含了原来叶子节点 $L$ 中的所有条目与新条目。

   将 $N$ 设为 $L$，设 $P$ 为 $N$ 的父节点，$EN$ 为父节点 $P$ 中指向 $N$ 的条目。调整 $EN.I$ 以保证所有在 $N$ 中的条目都被恰好包围。

   创建一个指向 $NN$ 的条目 $ENN$。如果 $P$ 有空间来存放 $ENN$，则将 $ENN$ 添加到 $P$ 中。如果没有，则对 $P$ 进行分裂操作得到 $P$

   和 $PP$。设 $N$ 为 $P$，$NN$ 为 $PP$，按相同的规则继续向上层传播。

   如果结点分裂，且该分裂向上传播导致了根结点的分裂，那么需要创建一个新的根结点，并且让它的两个孩子结点分别为原来那个根结点分裂

   后的两个结点，$R$ 树增高，程序结束。

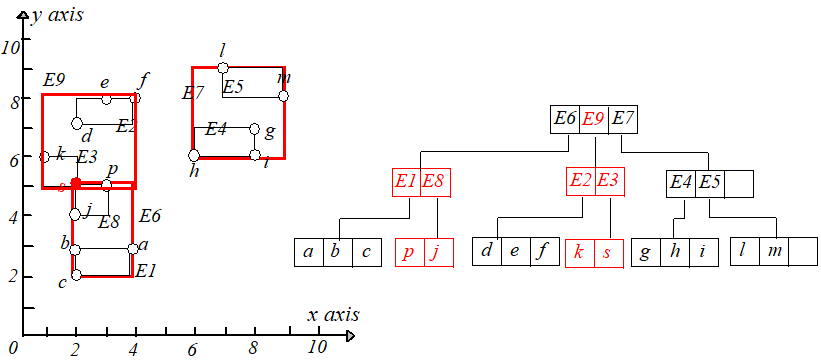
   举个例子，假设 $M=3$，把点 $p(3,5)$ 插入到 $R$ 树中，根据最小调整代价原则，最终选择将点 $p$ 插入到 $E3$ 中。如下图所示。

   

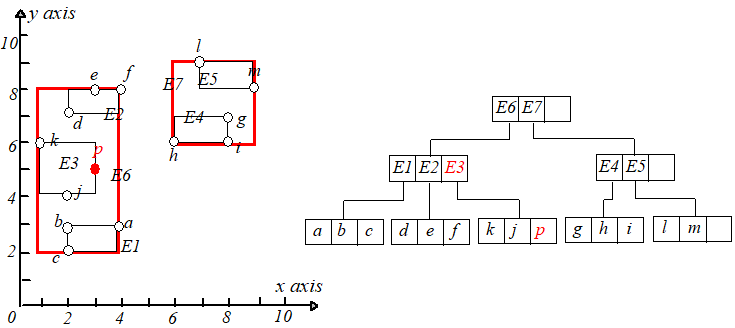
   接下来继续插入点 $s(2,5)$，点 $s$ 应该被插入到 $E3$ 指向的叶子节点中，但是插入后该叶子节点的条目变成了 $4$(>M)，于是需要进行节点分裂。

   将 $k,s,j,p$ 分裂为两个叶子节点，分别包含 $k,s$ 和 $j,p$，并调整 $E3.I$，然后为新节点(包含 $j,p$)创建一个新条目 $E8$。

      

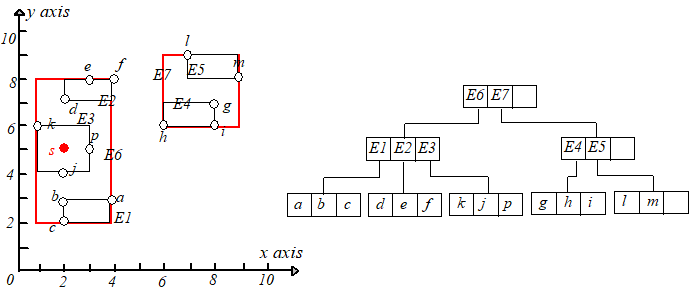
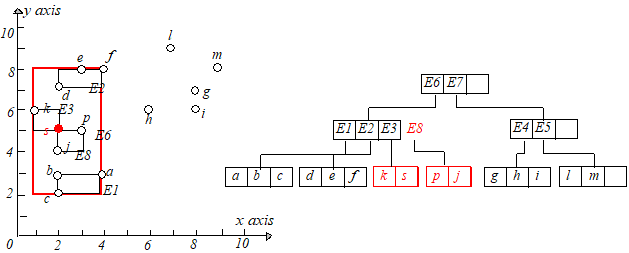
   但是 $E8$ 和 $E1,E2,E3$ 放在一起又会时节点条目数超过 $M$，所以需要再进行节点分裂，根据最小 $MBR$ 原则，将 $E2,E3$ 放到一起，$E1,E8$

   放到一起，调整 $E6.I$ 的大小使其适配节点 $E2,E3$，为节点 $E1,E8$ 创建一个新的条目 $E9$，插入到根节点，如下图所示：

   

2. 插入一棵 $R$ 树

   插入一棵 $R$ 树其实插入的是 $R$ 树根节点所有条目所表示的矩形。和插入一个点一样，在选择条目的时候都是采用扩张最小代价原则。

   不同的是：插入一个点，最终是一定会插入到叶子节点中，但是插入 $R$ 树的时候，由于 $R$ 树本身有高度，假设它的高度为 $H$，那么

   该它会被插入到 $Level \; H$ 层。

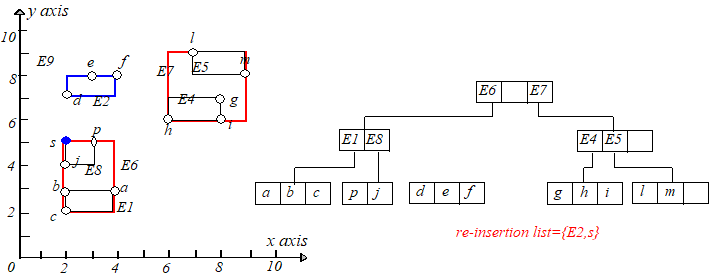
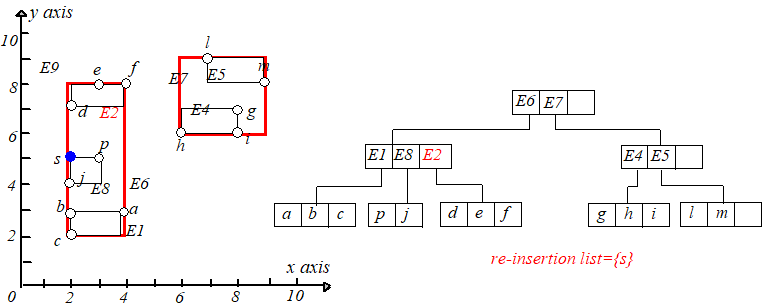
   举个例子，向树中插入 $E2$ 这课 $R$ 树，因为它的高度为 $2$，所以 $E2$ 会被插入到 $Level \; 2$。

      

 

R-tree 删除

从 $R$ 树中删除一个点，首先需要找到该点所在的叶子节点，通过判断点是否在条目所对应的矩形区域内来选择分支，直到找到叶子

节点，判断所要删除的点是否在该叶子节点内，如果在则删除，并调整父节点对应题目的矩形。删除之后，如果叶子节点剩余条目数过

少，即小于要求的最小值 $m$，则需要进行调整，令 $N$ 为条目数低于下限的叶子节点，调整步骤如下。

初始化一个用于存储被删除结点包含的条目的链表 $Q$。令 $P$ 为 $N$ 的父结点，$EN$ 为 $P$ 结点中存储的指向 $N$ 的条目。

因为 $N$ 含有条目数少于 $m$，于是从 $P$ 中删除 $EN$，并把结点 $N$ 中的条目添加入链表 $Q$ 中，然后输出节点 $N$。

往上层走，令 $N$ 等于 $P$，继续进行下溢判断，如果下溢，则将该节点中的每个条目加到 $Q$ 中，删除该结点和父节点中对应条目。

如果没有下溢，不要忘记调整祖父节点对应条目的矩形形状。

所有在 $Q$ 中的结点中的条目需要被重新插入。原来属于叶子结点的条目可以使用 Insert 操作进行重新插入，而那些属于非叶子结点

的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层(相当于插入一棵 $R$ 树)。

举个例子，删除点 $k(1,6)$，从根节点开始找，可以找到 $E3$，将其删除，但是下溢了。具体过程如下图：

       

       

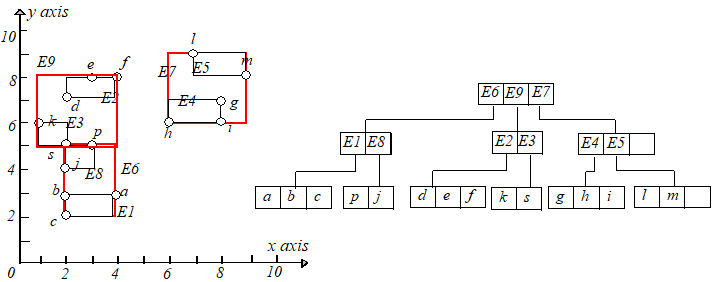
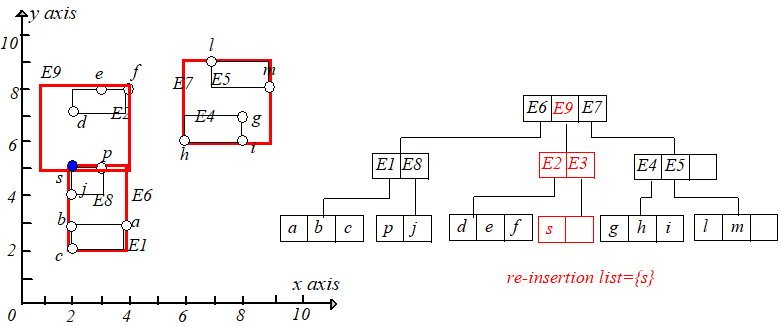
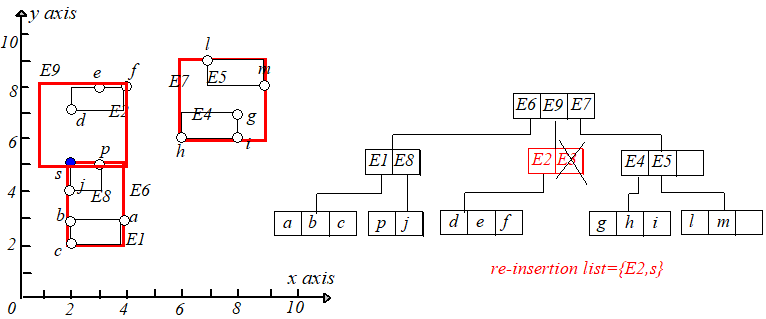
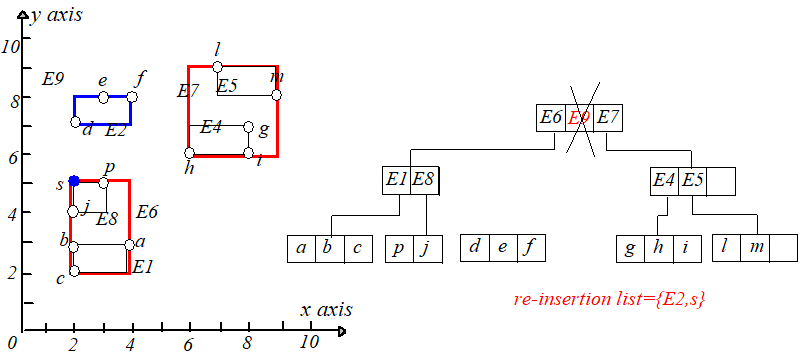
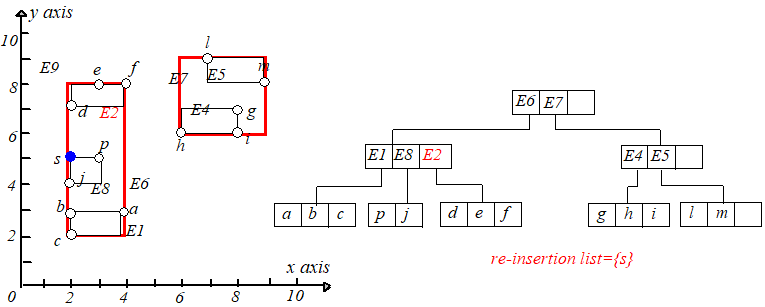
接下来将 $Q$ 中的项重新插入到 $R$ 树中。