B树和B+树
树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树,多叉就是多个分支的意思,二叉树就是最多只有两个分支的树。
如下图所示,即是一棵 树。
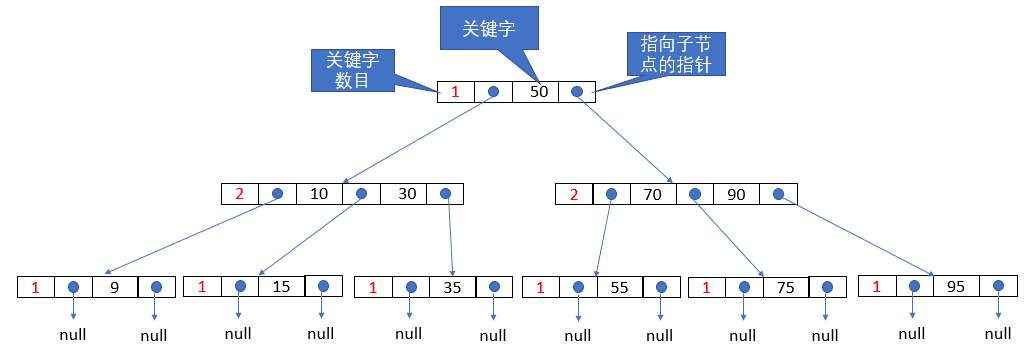
一棵 阶的 树必须满足如下条件:
1)每个结点最多含有 个分支,也就是说:每个节点最多 个关键字。
2)根节点最少可以有 个关键字,其它节点最少有 个关键字。
3)每个节点的内部结构为: 为节点中关键字的个数, 为关键字,从小到大排列, 为指向关键字满足
范围的孩子节点。
![]()
这里认为上面的 树高度为 ,第三层就是叶子节点,至于有些材料说那些 是叶子节点,简直扯淡。
树的节点类型定义如下,这个定义只是用来查找内存数据的,如果用来查找外存,代码需要调整一下,下面叙述。
1 2 3 4 5 6 7 8 | typedef int KeyType;struct BTNode { int keyNum; // 关键字个数 struct BTNode *parent; // 指向父节点 struct BTNode **ptr; // 子树指针向量, ptr[0],ptr[1],...,ptr[keyNum] KeyType **key; // 关键字向量, key[0],key[1],...,key[keyNum-1]} |
树设计的目的是用来查找磁盘的,为了简单,假设每个盘块正好存放一个 树的结点,这里用少量数据构造一棵 叉树的形式,来描述文件查
找的具体过程。
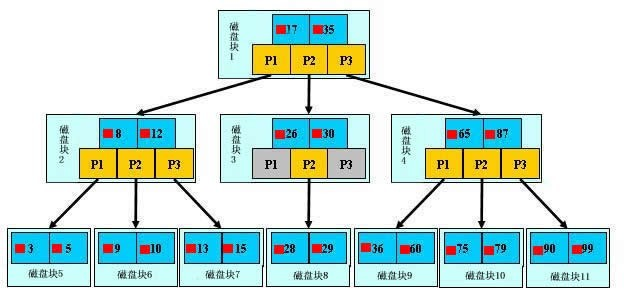
上面的图中比如根结点,其中 表示一个磁盘文件的文件名;小红方块表示这个 文件内容在硬盘中的存储位置; 表示指向 左子树的指针。
此时节点类型定义如下:
1 2 3 4 5 6 7 8 9 | typedef char* KeyType;struct BTNode { int keyNum; // 关键字个数 struct BTNode *parent; // 指向父节点 struct BTNode **ptr; // 子树指针向量, ptr[0],ptr[1],...,ptr[keyNum],每个元素存放另外一个盘块的地址 KeyType **key; // 关键字向量, 存储的是文件名 FILE_HARD_ADDR *offset; // 存储每个文件(关键字)的磁盘地址} |
下面来模拟下查找文件 的过程:
1)根据根结点指针找到文件目录的根磁盘块 ,将其中的信息导入内存。【磁盘 操作 次】
2)此时内存中有两个文件名 、 和三个存储其他磁盘页面地址的数据。根据算法我们发现:,因此我们找到指针 。
3)根据 指针,我们定位到磁盘块 ,并将其中的信息导入内存。【磁盘 操作 次】
4)此时内存中有两个文件名 、 和三个存储其他磁盘页面地址的数据。根据算法我们发现:,因此我们找到指针 。
5)根据 指针,我们定位到磁盘块 ,并将其中的信息导入内存。【磁盘 操作 次】
6)此时内存中有两个文件名 、。根据算法我们查找到文件名 ,并定位了该文件内存的磁盘地址。
分析上面的过程,发现需要 次磁盘 操作和 次内存查找操作。关于内存中的文件名查找,由于是一个有序表结构,可以利用折半查找提高效率。
至于 操作是影响整个 树查找效率的决定因素。
根据上面的例子我们可以看出,对于辅存做 读的次数取决于 树的高度。而 树的高度由什么决定的呢?
问题:一棵 阶 树,关键字个数为 ,求高度 (不包含叶子节点)的取值范围。
1)要使高度 最小,则每个节点的分支数均取上限 ,此时的 树就是一个完全 叉树,此时高度为
2)要使 最大,则每个节点的分支数均取下限 (根)或者 (非根),此时每层的节点个数为:
所以
所以
树的插入:因为关键字个数可能超过 ,故涉及拆分操作。规则如下:
a. 定位:利用 树查找算法,找出插入这个关键字的最低层中的某个非叶结点( 树中插入关键字一定插入在最低层非叶结点内)。
b. 插入:在 树中,每个非失败结点的关键字个数都在 之间,当插入后的结点关键字个数小于 ,
则可以直接插入;插入后检查被插入节点内关键字的个数,当插入后的结点关键字个数大于 时,则必须对结点进行分裂。
分裂的方法是:取一个新结点,将插入 key 后的原结点从中间位置将其中的关键字分为两部分,左部分包含的关键字放在原结点中,
右部分包含的关键字放到新的结点中,中间位置()的结点插入到原结点的父结点中。若此时导致其父结点的关键字个
数也超过了上限,则继续进行这种分裂操作,直至这个过程传到根节点为止,这样导致 树高度增 。
树的删除:因为关键字的个数可能小于 ,故涉及合并操作。规则如下:
a. 当被删除的关键字在终端节点。
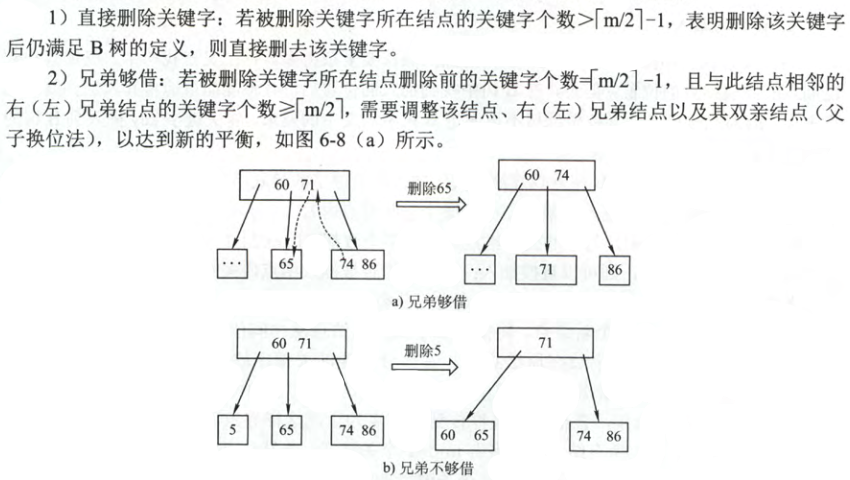

无论是兄弟够借还是兄弟不够借,都要让父节点的一个关键字下来,如果兄弟够借,则让兄弟还父节点一个关键字,否则就不还了,
并且将自身、兄弟节点与借下来的关键字合并。如果没有还父节点一个关键字,此时需要递归判断父节点是否违背了条件。若违反条
件则继续让祖父节点中的关键字先来,然后又是兄弟够不够借的问题。
b. 当被删除的关键字不在终端节点:用需要被删除关键字的前驱关键字或后继关键字替换后,会变成情况 。
找前驱:就是从关键字 所在节点的左子树一直往右找。找后继:从关键字 所在节点的右子树一直往左找。举个例子:
如下图,要删除的项在非叶子节点上。比如删除关键字 。
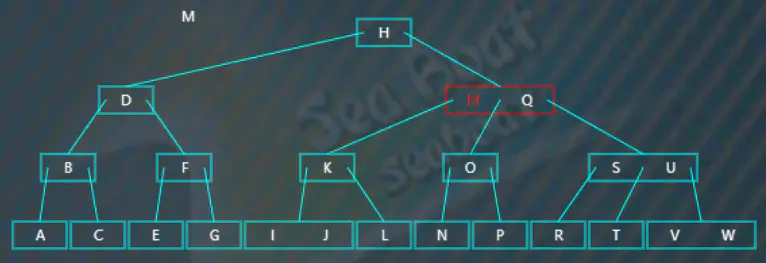
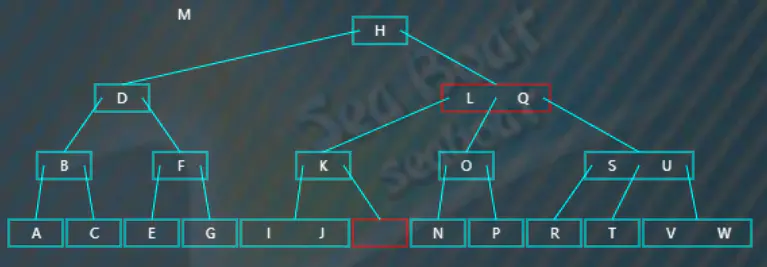
找到对应的中序前驱,从关键字 左边的指针指向的左子树开始一直往右走,最终可以找到前驱为 ,将 做个交换,此时
在叶子节点上,删除 ,如上右图。删除之后树不平衡,但发现兄弟节点可以借项给它,按照情况 进行调整即可,调整后如下图:
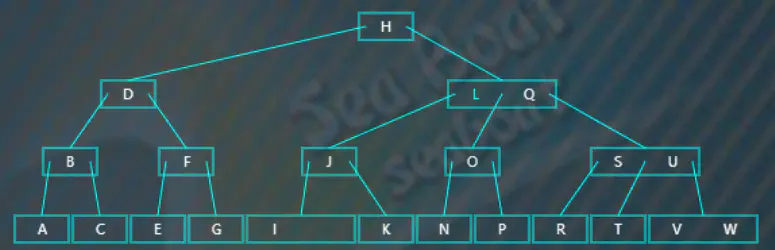
树:是应文件系统所需而产生的一种 树的变形树。一棵 阶的 树和 阶的 树的异同点在于:
1)每个节点分支数和 树一致。
2) 树节点内关键字的个数就等于该节点的分支数,而不是如 树那样减 。
3) 树改进了 树, 让内结点只作索引使用, 去掉了其中指向 data record 的指针, 使得每个结点中能够存放更多的 key, 因此能有更大的出度。
下面左图是 树,右图是 树。data 就是文件地址。
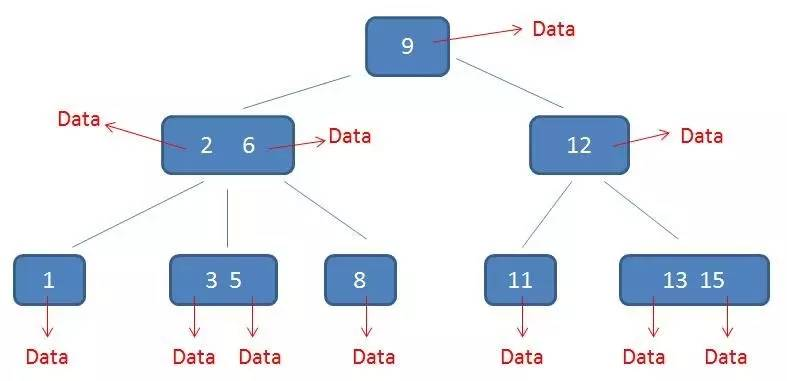
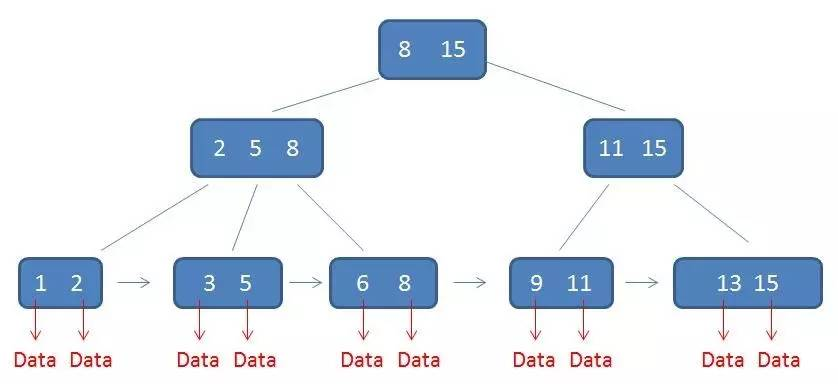
4)所有父节点的元素都同时存在于子节点,是子节点中是最大(或最小)元素。举个例子:
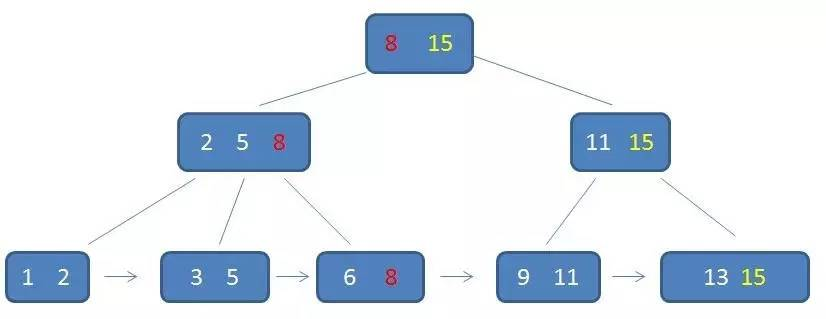
在上面这棵树中,根节点的元素 是节点 和 节点 的最大元素, 也是一样的。
5)由于 4),所以 树的叶子节点会包含全部的关键字信息,并且每个叶子节点包含指向相应记录的指针,所有叶子节点形成一个链表。
为什么说 树比 树更适合实际应用中操作系统的文件索引和数据库索引?
1) 树的磁盘读写代价更低: 树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对 树更小。如果把所有同一内
部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说
读写次数也就降低了。
2) 树的查询效率更加稳定:由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须
走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架