深度神经网络(DNN)
DNN 其实就是多层感知机,并没有什么特殊的地方。
DNN 按不同层的位置划分,其内部的神经网络层可以分为三类,输入层,隐藏层和输出层,如下图示例,一般来说第一层是输入层,最后一层是输出层,
而中间的层数都是隐藏层。
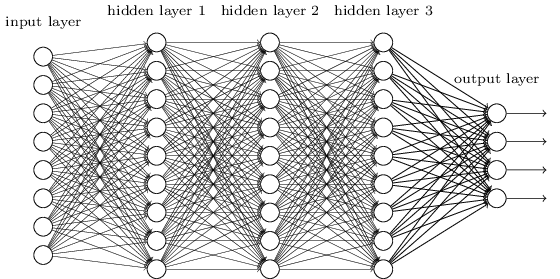
层与层之间是全连接的,也就是说,第 $i$ 层的任意一个神经元一定与第 $i+1$ 层的任意一个神经元相连。虽然 DNN 看起来很复杂,但是从小的
局部模型来说,还是和感知机一样,即一个线性关系 $z=\sum\limits w_ix_i + b$ 加上一个激活函数 $\sigma(z)$。
由于 DNN 层数多,则我们的线性关系系数 $w$ 和偏倚 $b$ 的数量也就是很多了。这里规定它的一种定义方式,以便下面的公式推导。
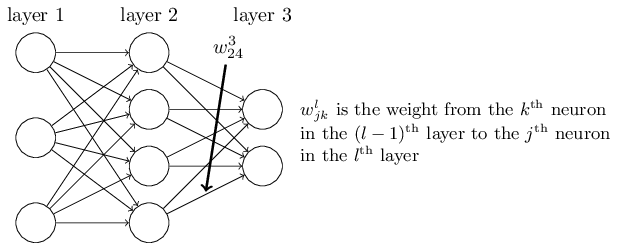
以下图一个三层的 DNN 为例,第二层的第 $4$ 个神经元到第三层的第 $2$ 个神经元的线性系数定义为 $w_{24}^3$。上标 $3$ 代表线性系数 $w$ 所在的层数,
而下标对应的是输出的第三层索引 $2$ 和输入的第二层索引 $4$。那为什么不是 $w_{42}^3$, 而是 $w_{24}^3$ 呢?这主要是为了便于模型用于矩阵表示运算,如果
是 $w_{42}^3$ 而每次进行矩阵运算是 $W^Tx+b$,需要进行转置。将输出的索引放在前面的话,则线性运算不用转置,即直接为 $Wx+b$。
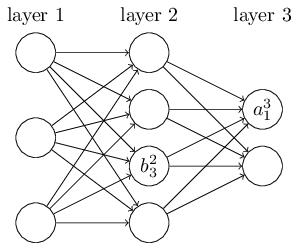
同样地,第二层的第三个神经元对应的偏置定义为 $b^2_3$。其中,上标 $2$ 代表所在的层数,下标 $3$ 代表偏倚所在的神经元的索引。 第三层的第一个
神经元对应的输出定义为 $a^3_1$。
深度神经网络前向传播过程
输入:总层数 $L$,所有隐藏层和输出层对应的矩阵 $W$,偏置向量 $b$,输入值向量 $x$。
输出:输出层的输出 $a^L$。
1)初始化 $a^1 = x$
2)for $l=2$ to $L$, 计算:
$$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$
注:$a^l$ 是一个向量,其维度等于该层神经元个数 $n_l$,$W^l$ 是一个二维矩阵,其维度为 $n_l \times n_{l-1}$。
深度神经网络反向传播过程
使用最常见的均方差来度量损失为例。即对于每个样本,我们期望最小化下式:
$$J = \frac{1}{2}||a^L-y||_2^2$$
首先是输出层第 $L$ 层。输出层的 $W,b$ 满足下式:
$$a^L = \sigma(z^L) = \sigma(W^La^{L-1} + b^L)$$
求解 $W,b$ 的梯度为
$$\frac{\partial J}{\partial W^L} = [(a^L-y) \odot \sigma^{'}(z^L)](a^{L-1})^T$$
$$\frac{\partial J}{\partial b^L} =(a^L-y)\odot \sigma^{'}(z^L)$$
上式中有一个符号 $\odot$,它代表 $Hadamard$ 积。
上面的求导结果如果看不懂,可画出神经网络(如下图),按标量一个一个求,然后将结果组合即可。或者先去阅读博客。
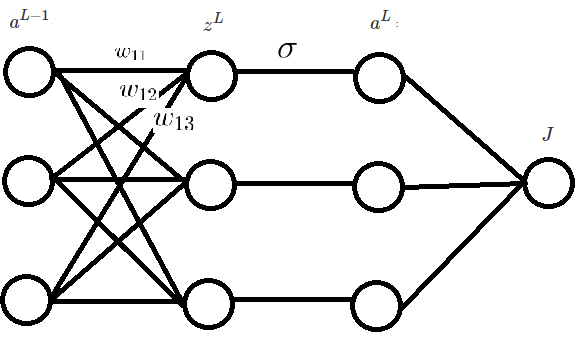
误差函数 $J$ 对第 $l$ 层的参数 $W^l,b^l$ 的梯度如下:
$$\frac{\partial J}{\partial W^l} = \frac{\partial J}{\partial z^l}(a^{l-1})^T$$
$$\frac{\partial J}{\partial b^l} = \frac{\partial J}{\partial z^l}$$
记
$$\delta^l = \frac{\partial J}{\partial z^l}$$
由第 $L$ 层参数的偏导数可知:
$$\delta^L = \frac{\partial J}{\partial z^L} = (a^L-y)\odot \sigma^{'}(z^L)$$
现在我们只需要得到 $\delta^l$ 和 $\delta^{l+1}$ 之间的关系就可以写出任一层的参数偏导数。
注意到:
$$\delta^{l} = \frac{\partial J}{\partial z^l} = (\frac{\partial z^{l+1}}{\partial z^{l}})^T\frac{\partial J}{\partial z^{l+1}} =(\frac{\partial z^{l+1}}{\partial z^{l}})^T \delta^{l+1}$$
其中
$$\frac{\partial z^{l+1}}{\partial z^{l}} = W^{l+1}diag(\sigma^{'}(z^l))$$
上面这个递推式可能不容易理解。可以画出对应神经网络,如下图所示,也是先按标量来求导,然后再组合。
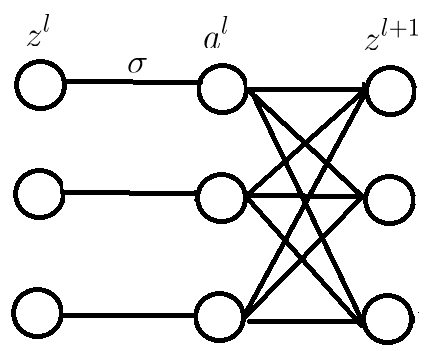
最终递推关系式为
$$\delta^{l} = (\frac{\partial z^{l+1}}{\partial z^{l}})^T\frac{\partial J}{\partial z^{l+1}} =
diag(\sigma^{'}(z^l))(W^{l+1})^T\delta^{l+1} =(W^{l+1})^T\delta^{l+1}\odot \sigma^{'}(z^l)$$


