卷积神经网络(CNN)
这个神经网络主要是针对图像的。
图像卷积
信号卷积本质上就是:$t$ 时刻的系统输出应该为 $t$ 时刻之前冲击信号在 $t$ 时刻响应的叠加。如果不懂可先去阅读博客:信号卷积。
信号卷积的离散形式定义为
$$(f*g)(t) = \sum_{\tau = -\infty}^{+\infty}f(\tau)g(t - \tau)$$
这里的 $f(t)$ 理解为冲击信号在不同时刻 $t$ 发生的次数,$g(t)$ 理解为冲击响应,即一个冲击信号经过一个线性系统后随时间变化的输出函数。
计算机中的图像经过采样量化之后也是一个离散的信号,可以类比信号卷积来定义图像卷积,区别在于:信号卷积刻画的是时间累计影响,
图像卷积刻画的是空间累计影响。下图展示了图像卷积的过程:
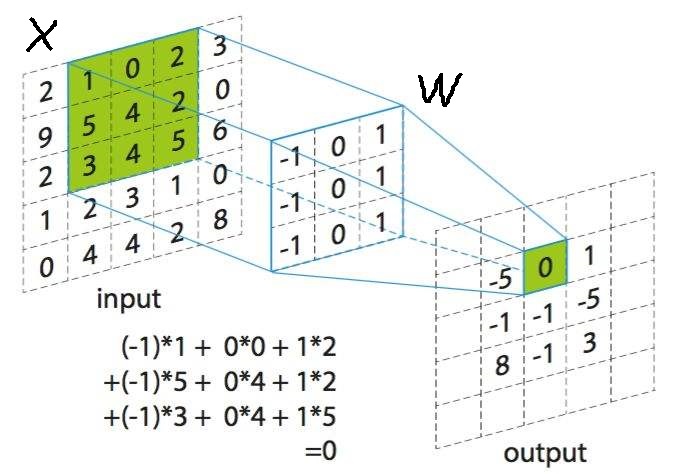
$X_{5 \times 5}$ 是一张单通道的图像,$X$ 可类比为函数 $f(t)$,每个像素 $X(i,j)$ 理解为冲击信号在空间中不同位置发生的次数。
$W_{3 \times 3}$ 是我们定义的卷积核,$W$ 可类比于函数 $g(t)$,每个元素 $W(i,j)$ 理解为冲击响应,即一个冲击信号经过一个线性系统后随空间变化的输出函数。
设输入图像 $X_{m \times n}$,卷积核 $W_{a \times b}$,矩阵 $Y$ 为输出图像,那么 $X$ 与 $W$ 的卷积定义如下:
$$Y(s,t) = (X*W)(s,t) = \sum_{i=0}^{m-1}\sum_{j=0}^{n-1}X(s+i, t+j)W(i,j)$$
用 $i,j$ 遍历卷积核 $W$,用 $s,t$ 遍历输出图像 $Y$,对整张图像的卷积就是用卷积核对图像进行窗口滑动的结果。易知:
$$\left\{\begin{matrix}
0 \leq s \leq m - a \\
0 \leq t \leq n - b
\end{matrix}\right.$$
即卷积后的矩阵 $Y$ 形状为 $(m - a + 1) \times (n - b + 1)$。
如果是三通道的 $RGB$ 图像该怎么做卷积呢?做法就是:每个通道都配一个卷积核,然后每个通道的图像和对应的卷积核做卷积,最后将 $3$ 个输出矩阵相加。
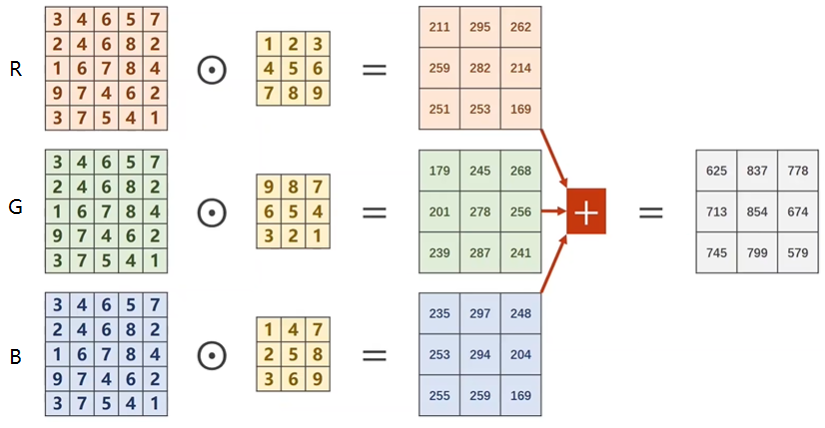
输入图像有几个通道,就需要为图像配几个卷积核,这几个卷积核称为一组卷积核。显然一组卷积核和图像做完卷积之后,输出图像就变成单通道的了。
如果想要卷积之后的输出图像也是多通道的该怎么做呢?显然只要多来几组卷积核就可以了,$m$ 组卷积核,输出图像就是 $m$ 通道的。

图像 Padding
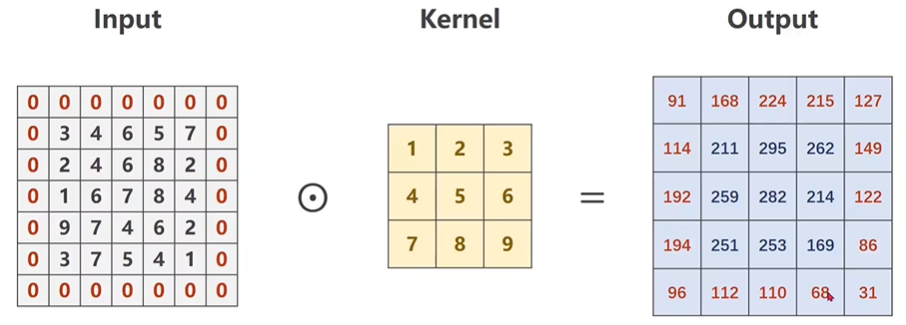
这个就是对图像的边界进行填充 $0$ 的操作,以满足某些形状要求。举个例子:输入图像大小为 $5 \times 5$,卷积核尺寸为 $3 \times 3$,卷积完成后
输出图像的尺寸为 $3 \times 3$,如果想要使输出图像尺寸为 $5 \times 5$ 该怎么办?这时就要用到 padding,只需要在输入图像周围填充一圈 $0$,使其
尺寸变成 $7 \times 7$ 即可。
图像池化
池化,也即降采样(subsample),降低数据的大小。这个名词本身可以这么理解:原来的数据好比大海,将大海变成水池,即意味着降低了数据量。
不断池化,表示将水池逐渐变小。池化操作对图像每个通道的数据独立,规模一般为 $2 \times 2$,通常夹在连续的卷积层中间, 用于压缩数据和参数的量,
减小过拟合。池化层进行的运算常用的有以下几种:
1)最大池化(Max Pooling):取 $4$ 个点的最大值。这是最常用的池化方法。
2)均值池化(Mean Pooling):取 $4$ 个点的均值。

卷积神经网络层级结构
使用全连接神经网络处理图像的最大问题在于全连接层的参数太多。对于 MNIST 数据,每一张图片的大小是 28*28*1,其中 28*28 是图片的大小,
1 表示图像是黑白的,只有一个色彩通道。假设第一层隐藏层的节点数为 500 个,那么一个全连接层的神经网络将有 28*28*500+500=392500 个参数。
当图片更大时,比如在 Cifar-10 数据集中,图片的大小为 32*32*3,其中 32*32 表示图片的大小,*3 表示图片是通过红绿蓝三个色彩通道表示的。
这样输入层就是 3072 个节点,如果第一次全连接层仍然是 500 个节点,那么这一层全连接神经网络将有 32*32*3*500+500=150 万个参数。参数增多
除了导致计算速度减慢,还很容易导致过拟合问题。所以需要一个更合理的神经网络结构来有效的减少神经网络中参数个数。而卷积神经网络就可以达
到这个目的。
卷积神经网络的神经元有一些不同:
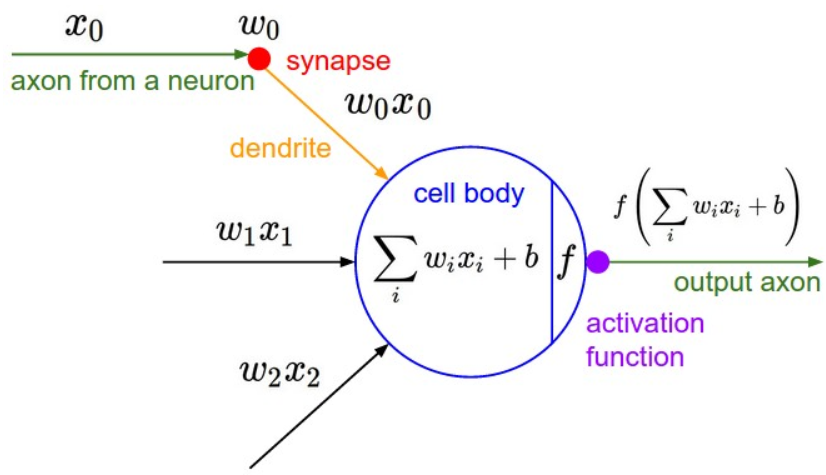
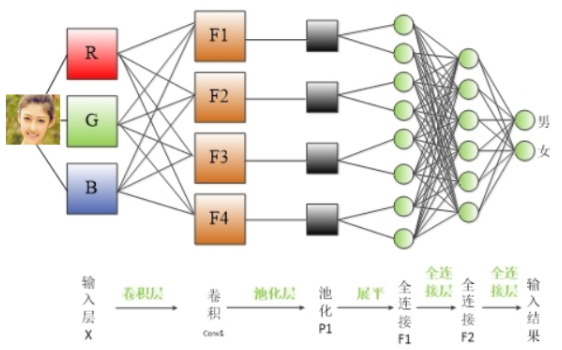
每一个神经元的 $w,x,b$ 都不再是一个标量,而是张量。$w_{i}$ 是一个二维的卷积核,$x_{i}$ 是一张二维的图片,$w_{i}x_{i}$ 进行的操作也不是相乘,而是矩阵的
卷积,每个神经元表示一个通道的图像,每层有几个神经元代表该层输出图像是几个通道的。连接到同一个神经元的卷积核 $w_{1},w_{2},w_{3}$ 构成一组卷积核。
网络结构如上右图所示。
可以看出每一个卷积核 $w_{i}$ 所连接的都是一个通道的图像,或者说一个通道的图像数据都共享了同一个卷积核。
卷积神经网络的输出是接一个全连接层(设神经元个数为 $n$),因为两者的神经元结构不一样,所以卷积神经网络的输出需要 $review$ 成一个形状为
$(batchSize, n)$ 的二维张量后才能喂给全连接神经网络。
卷积层 + 池化层 + 激活函数是卷积神经网络最基本的结构,激活函数也可以放到卷积层后面,这样池化层就不再接激活函数了,即:
卷积层 + 激活函数 + 池化层。举个例子:
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320, 10)
def forward(self, x):
# flatten data from (n,1,28,28) to (n, 784)
batch_size = x.size(0)
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
x = x.view(batch_size, -1) # -1 此处自动算出的是320
x = self.fc(x)
return x
卷积神经网络前向传播过程
这个可以和深度神经网络做一个对比。
$CNN$ 中 $a^l$ 不再是一个向量,而是一个三维张量 $C \times H \times W$,其中 $C$ 表示通道数,也是该层神经元个数,即 $C = n_l$。每个神经元的
输出 $a^l_i$ 不是一个标量元素,而是一个二维张量 $H \times W$,即矩阵,表示的是一个通道的图像数据。$DNN$ 中 $W_l$ 是一个二维矩阵,$CNN$ 中
$W_l$ 的形状为 $n_l \times n_{l-1} \times height \times width$,$n_{l-1}$ 表示上一层的神经元个数,即上一层输出图像的通道数,$n_l$ 表示当前层的神经元个数,即当
前层输出图像的通道数,$height \times width$ 表示一个卷积核的形状,一组卷积核就是形状为 $n_{l-1} \times height \times width$ 的张量。
总结:
1)$a^l$ 形状为 $(n_l,H,W)$,$H,W$ 的值取决于上一层的输出图像尺寸和卷积核尺寸。
2)$W_l$ 形状为 $(n_l,n_{l-1},height,width)$。卷积核尺寸 $height,width$ 需要自定义。
算法过程如下:
1)初始化 $a^1$ 为一张 $RGB$ 图像数据。
2)for $l=2$ to $L$, 计算:
a. 如果 $a^l$ 是卷积层,则输出
$$a^l= ReLU(z^l) = ReLU(a^{l-1}*W^l +b^l)$$
其中,上标代表层数,星号代表卷积,而 $b$ 代表我们的偏置,,采用 $ReLU$ 作为激活函数。
b. 如果第 $l$ 层是池化层,则输出为 $a^l=pool(a^{l-1})$, 这里的 $pool$ 指按照池化区域大小 $k$ 和池化标准将输入张量缩小的过程。
卷积神经网络反向传播过程
要明白卷积操作是用来干嘛的,是用来提取特征的,反向传播的意义又是什么?因为初始的时候卷积核的值都是随机设定的,我们可以根据前向
传播的预测结果,进行误差分析,不断地修改卷积核的值,使得更好的提取特征,就是反向传播的意义。
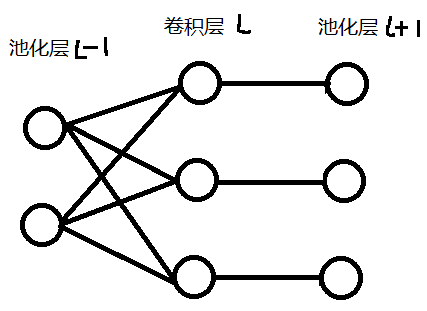
卷积层的激活函数为 $f(x) = relu(x)$,池化层没有激活函数,或者可以认为激活函数为 $f(x) = x$。
我们将每一层的神经网络再分成两部分,以第 $l$ 层为例,设 $z^l$ 为激活函数作用前的输出,$a^l$ 为激活函数作用后的输出,令
$$\delta^l = \frac{\partial J}{\partial z^l}$$
从池化层反向传播到卷积层
现在已经知道误差函数 $J$ 对 $l+1$ 层池化层的偏导数为 $\delta^{l+1}$,如何求 $J$ 对 $l$ 层卷积层的偏导数(激活函数作用之前) $\delta^l$?
池化层一般我们会用 $MAX$ 或者 $Average$ 对输入进行池化,池化的区域大小已知。现在我们反过来,要从池化后的误差 $\delta^{l+1}$,还原前一次较大区域对应的误差。
举个例子:假设我们的池化区域大小是 $2 \times 2$。$\delta^{l+1}$ 的第 $k$ 个子矩阵为:
$$\delta_k^{l+1} = \left( \begin{array}{ccc} 2& 8 \\ 4& 6 \end{array} \right)$$
如果是 $Max$,假设我们之前在前向传播时记录的最大值位置分别是左上,右下,右上,左下,则转换后的矩阵为:
$$\left( \begin{array}{ccc} 2&0&0&0 \\ 0&0& 0&8 \\ 0&4&0&0 \\ 0&0&6&0 \end{array} \right)$$
如果是 $Average$,则进行平均,转换后的矩阵为:
$$\left( \begin{array}{ccc} 0.5&0.5&2&2 \\ 0.5&0.5&2&2 \\ 1&1&1.5&1.5 \\ 1&1&1.5&1.5 \end{array} \right)$$
所以
$$\delta_k^{l} = upsample(\delta_k^{l+1}) \odot \sigma^{'}(z_k^{l})$$
这里的激活函数是 $relu$,所以
$$\delta^{l} = upsample(\delta^{l+1}) \odot \sigma^{'}(z^{l})$$
从卷积层反向传播到池化层
现在已经知道误差函数 $J$ 对 $l$ 层卷积层(激活函数作用之前)的偏导数为 $\delta^{l}$,如何求 $J$ 对 $l-1$ 层池化层的偏导数 $\delta^{l-1}$?
卷积层的前向传播公式为
$$z^l = a^{l-1}*W^l +b^l =\sigma(z^{l-1})*W^l +b^l$$
这里的激活函数是池化层输出的激活函数,即 $f(x) = x$。
以 $l−1$ 层输出的第 $1$ 个矩阵, $l$ 层的第 $2$ 个矩阵为例,假设 $a^{l−1}_1$ 是一个 $3 \times 3$ 矩阵,卷积核 $W_{21}$ 是一个 $2 \times 2$ 的矩阵,采用 $1$ 步幅,卷积过程如下:
$$\left( \begin{array}{ccc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{array} \right) *
\left( \begin{array}{ccc} w_{11}&w_{12}\\ w_{21}&w_{22} \end{array} \right) = \left( \begin{array}{ccc} z_{11}&z_{12}\\
z_{21}&z_{22} \end{array} \right)$$
利用卷积的定义,很容易得出:
$$z_{11} = a_{11}w_{11} + a_{12}w_{12} + a_{21}w_{21} + a_{22}w_{22} \\
z_{12} = a_{12}w_{11} + a_{13}w_{12} + a_{22}w_{21} + a_{23}w_{22} \\
z_{21} = a_{21}w_{11} + a_{22}w_{12} + a_{31}w_{21} + a_{32}w_{22} \\
z_{22} = a_{22}w_{11} + a_{23}w_{12} + a_{32}w_{21} + a_{33}w_{22}$$
我们按标量一个个求,可以写出一个求导结果:

这个代表误差函数 $J$ 在如下红色路径的导数传播:
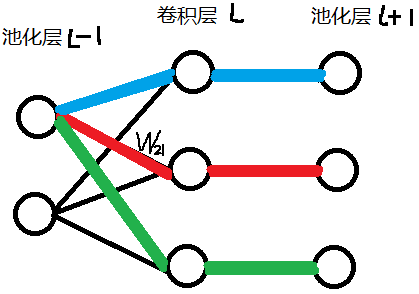
如果我们想要求出 $J$ 对 $a^{l-1}_1$ 的偏导数,还要求出蓝色路径和绿色路径的两个导数,然后三个导数矩阵相加即可。
这上面 $9$ 个式子其实可以用一个矩阵卷积的形式表示,即:
$$\left( \begin{array}{ccc} 0&0&0&0 \\ 0&\delta_{11}& \delta_{12}&0 \\ 0&\delta_{21}&\delta_{22}&0 \\ 0&0&0&0 \end{array} \right)
* \left( \begin{array}{ccc} w_{22}&w_{21}\\ w_{12}&w_{11} \end{array} \right) = \left( \begin{array}{ccc} \nabla a_{11}&\nabla
a_{12}&\nabla a_{13} \\ \nabla a_{21}&\nabla a_{22}&\nabla a_{23}\\ \nabla a_{31}&\nabla a_{32}&\nabla a_{33} \end{array} \right)$$
如果不对矩阵 $a^{l−1}_1$ 求导,而对卷积核 $W_{21}$ 求导,可以发现
$$\frac{\partial J}{\partial w_{11}} = a_{11}\delta_{11} + a_{12}\delta_{12} + a_{21}\delta_{21} + a_{22}\delta_{22} \\
\frac{\partial J}{\partial w_{12}} = a_{12}\delta_{11} + a_{13}\delta_{12} + a_{22}\delta_{21} + a_{23}\delta_{22} \\
\frac{\partial J}{\partial w_{21}} = a_{21}\delta_{11} + a_{22}\delta_{12} + a_{31}\delta_{21} + a_{32}\delta_{22} \\
\frac{\partial J}{\partial W_{22}} = a_{22}\delta_{11} + a_{23}\delta_{12} + a_{32}\delta_{21} + a_{33}\delta_{22} $$
写成卷积形式
$$\frac{\partial J}{\partial W_{21}} = \left( \begin{array}{ccc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}
\\ a_{31}&a_{32}&a_{33} \end{array} \right) * \left( \begin{array}{ccc} \delta_{11}& \delta_{12} \\ \delta_{21}
&\delta_{22} \end{array} \right)$$
这也太神奇了,但是我不知道怎么描述这一规律。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号