KL 散度和交叉熵
相对熵(relative entropy)就是 KL 散度(Kullback–Leibler divergence),用于衡量两个概率分布之间的差异。
举个例子:假设我们发现了一些太空蠕虫,这些太空蠕虫的牙齿数量各不相同。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高,
所以我们需要用尽量少的数据表达这些信息。其中一个办法是:不发送单个数值,而是绘制一张图表,其中 $X$ 轴表示所观察到的不同牙齿数量,$Y$ 轴是
看到的太空蠕虫具有 $x$ 颗牙齿的概率(具有 $x$ 颗牙齿的蠕虫数量/蠕虫总数量)。这样,我们就将观察结果转换成了分布。
但我们还能进一步压缩数据大小。我们可以用一个已知的分布来表示这个分布(比如均匀分布、二项分布、正态分布等)。
假设有 $100$ 只蠕虫,各种牙齿数的蠕虫的数量统计结果如下:
$$P(X=0) = 0.02 \;\;\;\;\; P(X=1) = 0.03 \\
P(X=2) = 0.05 \;\;\;\;\; P(X=3) = 0.14 \\
P(X=4) = 0.16 \;\;\;\;\; P(X=5) = 0.15 \\
P(X=6) = 0.12 \;\;\;\;\; P(X=7) = 0.08 \\
P(X=8) = 0.10 \;\;\;\;\; P(X=9) = 0.08 \\
P(X=10) = 0.07$$
1)假如我们用均匀分布来表示真实分布
离散随机变量的均匀分布只有一个参数:均匀概率;即给定事件发生的概率。
$$P(X=i) = 0.09, \; i=0,1,2,\cdots,10$$
均匀分布和我们的真实分布对比:
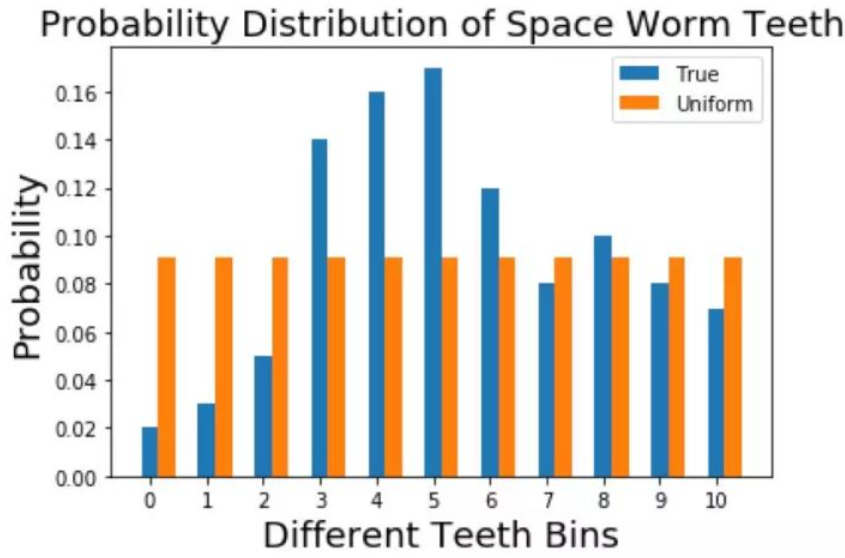
橙色是用来逼近的分布,蓝色是真实分布,这两个分布看上去明显差异比较大。
2)假如我们用二项分布来表示真实分布
二项分布为 $X \sim B(n,p)$。首先计算蠕虫的牙齿的期望:
$$EX = \sum_{i=0}^{10}i \cdot P(X = i) = 5.44$$
要想用二项分布来逼近这个分布,可以认为 $n = 10$(这里并没有什么含义,牙齿数量也不能当成试验次数,只是从形式上观察的),然后通过
$np = 10p = 5.44$,可解得 $n = 0.544$。真实分布和二项分布的比较如下:
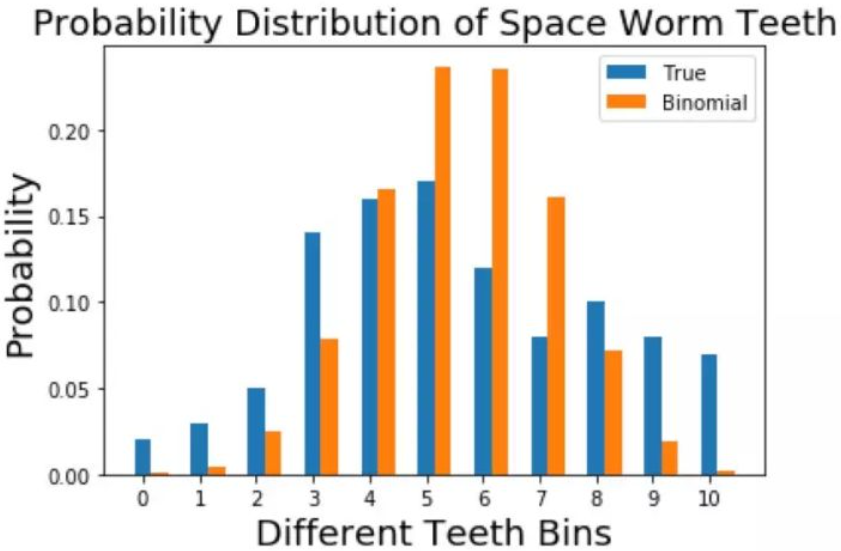
橙色所表示的分布和真实分布之间虽然还有差异,但是看起来要比用均匀分布去逼近好一点。
我们如何定量地确定哪个分布更好?
经过这些计算之后,我们需要一种衡量每个近似分布与真实分布之间匹配程度的方法。这就是 KL 散度的用武之地。KL 散度在形式上定义如下:
$$D_{KL}(p||q) = \sum_{i = 1}^{N}p(x_{i})\ln \frac{p(x_{i})}{q(x_{i})}$$
其中 $q(x)$ 是近似分布,$p(x)$ 是我们想要用 $q(x)$ 匹配的真实分布。直观地说,这衡量的是给定任意分布偏离真实分布的程度。如果两个分布
完全匹配,那么有
$$D_{KL}(p||q) = 0$$
计算上面两个分布和真实分布之间地 KL 散度,会发现均匀分布的匹配度更高,即 KL 散度值更小。
上面那个 KL 散度的定义是针对离散分布的,对于连续的分布,只不过就是将求和变成积分,概率改成概率密度,定义式如下:
$$D_{KL}(p||q) = \int p(x_{i})\ln \frac{p(x_{i})}{q(x_{i})} dx$$
接下来我们从熵的角度来理解一下 KL 散度,将离散分布的 KL 散度的定义式展开:
$$D_{KL}(p||q) = \sum_{i = 1}^{N}p(x_{i})\ln p(x_{i}) - \sum_{i = 1}^{N}p(x_{i})\ln q(x_{i}) \\
= -\sum_{i = 1}^{N}p(x_{i})\ln q(x_{i}) - \left (-\sum_{i = 1}^{N}p(x_{i})\ln p(x_{i}) \right )$$
信息量:任何事件都会承载着一定的信息量,我们可以通过事件发生的概率来定义事件的信息量,事件发生的概率越小,其信息量越大。也可以认为
一个事件结果的出现概率越低,对其编码的 bit 长度就越长,因为根据哈夫曼编码,概率低的事件,从根到表示该事件的叶子节点的路径就越长。这
里的 bit 长度就可以认为是信息量。事件 $X = x_{0}$ 发生所具有的信息量为
$$I(x_{0}) = -\ln p(x_{0})$$
所以式子中的 $-\ln p(x_{i}),\; -\ln q(x_{i})$ 就是代表在对应分布下,事件发生的信息量或编码长度。
信息熵:把所有可能事件罗列出来,就可以求得所有事件的信息量,进而可以求期望,信息量的期望就是熵,所以熵的公式为:
$$H(p) = -\sum_{i = 1}^{N}p(x_{i})\ln p(x_{i})$$
可以发现 KL 散度公式的第二部分就是信息熵。因为 $p(x)$ 本身就是真实分布,由这个分布所构建的哈夫曼树是最完美的,也是浪费最小的,所以信
息熵可以认为是:编码方案完美时,最短平均编码长度。
接下来观察一下 KL 散度定义式的第一项,$q(x_{i})$ 并不是真实分布,由于对概率分布的估计不一定正确,所以编码方案不一定完美,将这种情况下
的平均编码长度定义为交叉熵,即
$$H(p,q) = -\sum_{i = 1}^{N}p(x_{i})\ln q(x_{i})$$
所以 KL 散度其实就是
$$D_{KL}(p||q) = H(p,q) - H(p)$$
可以看出,相对熵其实就是:由于编码方案不一定完美,和数据的真实分布有差别,所导致的平均编码长度的增大值。
在机器学习中,因为交叉熵与相对熵只差一个真实分布的信息熵,而真实分布是固定的分布,与训练无关,所以可以将交叉熵作为损失函数进行优化。
证明:$D_{KL}(p || q) \geq 0$
以离散分布为例,由琴生不等式得
$$D_{KL}(p||q) = \sum_{i = 1}^{N}p(x_{i})\ln \frac{p(x_{i})}{q(x_{i})} = -\sum_{i = 1}^{N}p(x_{i})\ln \frac{q(x_{i})}{p(x_{i})} \\
\geq -\ln\left ( \sum_{i = 1}^{N}p(x_{i}) \frac{q(x_{i})}{p(x_{i})} \right ) = 0$$
交叉熵与最大似然估计的联系
离散分布的极大似然估计的表达式如下:
$$\theta = arg \; \max_{\theta} \prod_{i=1}^{n}q(x_{i} | \theta) \\
\Leftrightarrow \theta = arg \; \max_{\theta} \sum_{i=1}^{n}\ln q(x_{i} | \theta) \\
\Leftrightarrow \theta = arg \; \max_{\theta} \sum_{x \in X}^{}p(x)\ln q(x | \theta) \\
\Leftrightarrow \theta = arg \; \min_{\theta} H(p,q)$$
其中真实分布 $p$ 就是根据样本统计出来的,因为根本就不可能会知道真实分布的,只能用样本的分布情况作为总体的分布情况,然后
再去估计参数,所以极大似然估计等价于极小化交叉熵(会相差一个因子 $\frac{1}{N}$,但不影响最优解)。



