指数加权移动平均
加权移动平均法:是对观察值分别给予不同的权数,按不同权数求得移动平均值,并以最后的移动平均值为基础,确定预测值的方法。
采用加权移动平均法,是因为观察期的近期观察值对预测值有较大影响,它更能反映近期变化的趋势。
指数移动加权平均法:是指各数值的加权系数随时间呈指数式递减,越靠近当前时刻的数值加权系数就越大。
下面是一年 $365$ 天的温度散点图,以天数为横坐标,温度为纵坐标,可以看到各个小点分布在图上,有一定的曲线趋势,但是并不明显。
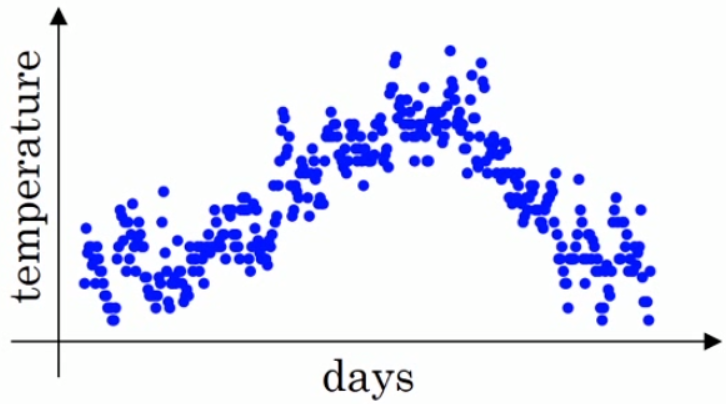
指数加权平均的表达式如下:
$$v_{t} = \beta v_{t - 1} + (1 - \beta)\theta_{t}$$
其中,$\theta_{t}$ 代表第 $t$ 天的温度值,$\beta$ 表示加权下降的速率,其值越小下降的越快,$v_{t}$ 为第 $t$ 天的移动加权平均值。
令 $v_{0} = 0$,将这个式子展开得:
$$v_{t} = \beta v_{t - 1} + (1 - \beta)\theta_{t} \\
= \beta\bigg [ \beta v_{t - 2} + (1 - \beta)\theta_{t-1} \bigg ] + (1 - \beta)\theta_{t} \\
= \beta^{2}v_{t - 2} + \beta(1 - \beta) \theta_{t-1} + (1 - \beta)\theta_{t}\\
= \beta^{2}\bigg [ \beta v_{t - 3} + (1 - \beta)\theta_{t-2} \bigg ] + \beta(1 - \beta) \theta_{t-1} + (1 - \beta)\theta_{t} \\
= \beta^{3} v_{t - 3} + \beta^{2}(1 - \beta)\theta_{t-2} + \beta(1 - \beta) \theta_{t-1} + (1 - \beta)\theta_{t} \\
\cdots \\
= \beta^{t}v_{0} + \beta^{t-1}(1 - \beta)\theta_{1} + \beta^{t-2}(1 - \beta) \theta_{2} + \cdots + (1 - \beta)\theta_{t} \\
= (1 - \beta) \sum_{i=1}^{t}\beta^{t-i}\theta_{i}$$
可以看到,计算第 $t$ 天的移动加权平均值 $v_{t}$ 其实就是第 $1$ 天到第 $t$ 天每天温度的加权和,每一天温度的权重系数为
$$(1 - \beta)\beta^{t-i}$$
$(1-\beta)$ 是一个常数,由 $(1-\beta)^{t-i}$ 可知:天数越靠近 $t$,$t - i$ 越小,$(1-\beta)^{t-i}$ 越大,即那一天温度对应的权值越大。
$\beta$ 越大,后项收到前项的影响越大,越平滑,但是适应新变化更加困难。
重要性质:一般而言,$v_{t}$ 是前 $\frac{1}{1-\beta}$ 天温度的指数加权平均值。易知极限:
$$\lim_{\varepsilon \rightarrow 0}\left ( 1 - \varepsilon \right )^{\frac{1}{\varepsilon}} = \frac{1}{e}$$
令
$$1 - \beta = \varepsilon$$
因为 $\beta$ 是在 $0-1$ 之间,所以 $1-\beta$ 可以认为趋于 $0$,于是有
$$\beta^{\frac{1}{1 - \beta}} \approx \frac{1}{e}$$
也就是说第 $t - \frac{1}{1 - \beta}$ 天的温度对 $v_{t}$ 的影响已经不足 $\frac{1}{e}$ 了,在这之前的温度影响都可以忽略了。
回到最初的那幅图,如果我们要看出这个温度的变化趋势,很明显需要做一点处理,我们用指数加权移动平均来平滑,取 $\beta = 0.9$,
然后计算出每个 $v_{t}$ 来代替 $\theta_{t}$,把所有的 $v$ 计算完之后画图,红线就是 $v$ 的曲线:
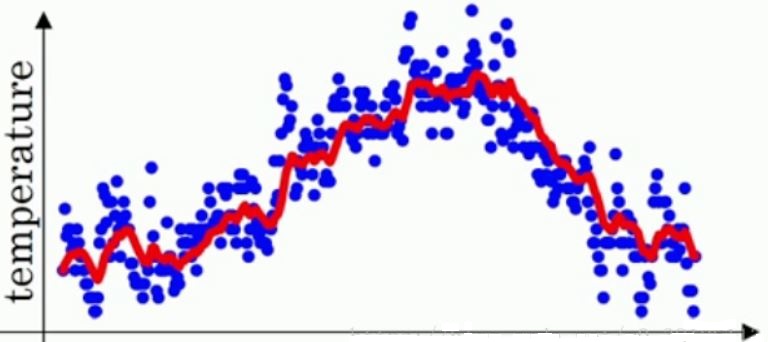
红色曲线第 $t$ 天的温度就约等于前 $10$ 天温度(蓝色散点图所记录)的平均值。现在增大 $\beta$,将其值改为 $0.98$,那么 $\frac{1}{1-\beta}$ = 50,
按照加权平均的性质,新的 $v_{t}$ 就代表前 $50$ 天的平均温度,求出所有 $v$ 值画出曲线,如图绿线所示:

可以明显看到绿线比红线的变化更迟,红线达到某一温度,绿线要过一阵子才能达到相同温度。因为绿线是前 $50$ 天的平均温度,变化就会
更加缓慢,而红线是最近 $10$ 天的平均温度,只要最近 $10$ 天的温度都是上升,红线很快就能跟着变化。
再看看另一个极端情况:$\beta$ 等于 $0.5$,意味着 $v_{t}$ 约为最近两天的平均温度,曲线为如下黄线:

可以看出黄色曲线和原本的温度很相似,但曲线的波动幅度也相当大!
滑动平均模型和深度学习有什么关系:
通常来说,我们的数据也会像上面的温度一样,具有不同的值,如果使用滑动平均模型,就可以使得整体数据变得更加平滑——这意味着数据的噪音会更少,
而且不会出现异常值。但是同时 $\beta$ 太大也会使得数据的曲线右移,和数据不拟合。需要不断尝试出一个 $\beta$ 值,既可以拟合数据集,又可以减少噪音。
滑动平均模型在深度学习中还有另一个优点:它只占用极少的内存。当你在模型中计算最近十天(有些情况下远大于十天)的平均值的时候,你需要在内存
中加载这十天的数据然后进行计算,但是指数加权平均值约等于最近十天的平均值,而且根据递推公式,你只需要提供 $\theta_{t}$ 这一天的数据,再加上 $v_{t-1}$
的值和 $\beta$ 值,相比起十天的数据这是相当小的数据量,同时占用更少的内存。
偏差修正:当 $\beta$ 等于 $0.98$ 的时候,还是用回上面的温度例子,曲线实际上不是像绿线一样,而是像紫线:
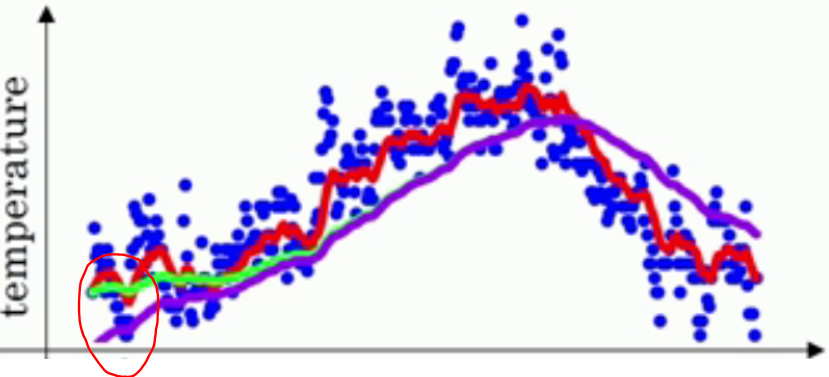
注意到在紫线刚刚开始的时候,曲线的值相当的低,这是因为在一开始的时候并没有前 $50$ 天的数据,而是只有寥寥几天的数据,相当于少加了几十天
的数据,所以 $v_{t}$ 的值很小,这和实际情况的差距是很大的,也就是出现的偏差。修正方法是:
$$v_{t} = \frac{\beta v_{t - 1} + (1 - \beta)\theta_{t}}{1 - \beta^{t}}$$
随着 $t$ 增加,$\beta^t$ 接近于 $0$,所以当 $t$ 很大的时候,偏差修正几乎没有作用,因此当 $t$ 较大的时候,紫线和绿线重合了。不过在开始学习
阶段,偏差修正可以更好地预测温度。


