基本不等式

不等式 $1$：

$$a^{2} + b^{2} \geq 2ab$$

从代数角度来证明：

$$(a - b)^{2} \geq 0 \\
\Rightarrow a^{2} -2ab + b^{2} \geq 0 \\
\Rightarrow a^{2} + b^{2} \geq 2ab$$

从几何角度来证明：

     

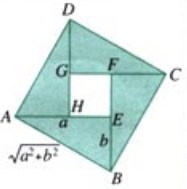
显然正方形 $ABCD$ 的面积会大于等于四个直角三角形的面积和，即

$$a^{2} + b^{2} \geq 2ab$$

当中间那块白色区域面积为 $0$ 的时候，显然正方向的面积等于四个三角形的面积和。

无论用代数还是几何，还是通过坐标系，向量，都可以描述一个问题，从而给出问题的证明，比如几何上的余弦定理就可以通过

向量和代数角度证明，关键是找到描述问题的方式。

 

不等式 $2$：

$$\sqrt{ab} \leq \frac{a + b}{2}, \; a \geq 0, b \geq 0$$

代数角度很好证明，利用不等式 $1$，令 $a = \sqrt{a},b = \sqrt{b}$，就有

$$a + b \geq 2 \sqrt{ab}$$

那么能找到这个问题的几何描述吗？关键在于如何用几何表示出 $\sqrt{ab}$。

     

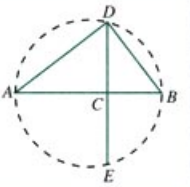
上面这个图，让 $AC = a, BC = b$，则 $\frac{a + b}{2} = R$，通过设一些变量很容易证明：$CD = \sqrt{ab}$，显然 $CD \leq R$，

当点 $C$ 在圆心时，$CD = R$。

在这个不等式里，几何描述并不是很容易，代数角度就比较容易证明。数学上的问题使用不同的角度或工具考虑，难易程度是不同的。