EM 算法原理
假设有两枚硬币 $A,B$，以相同的概率随机选择一个硬币，进行如下的掷硬币实验：共做 $5$ 次实验，每次实验独立的掷 $5$ 次。
下面左图是在知道每次选择的是硬币 $A$ 还是硬币 $B$ 的情况下的试验结果；右图是在不知道选择的是硬币 $A$ 还是硬币 $B$ 的情况下的试验结果。
问：在这两种情况下如何估计硬币 $A,B$ 正面出现的概率 $\theta_{A}$ 和 $\theta_{b}$？
做 $5$ 次独立重复试验，将观察到的样本表示为
$$Y = \left ( Y_{1},Y_{2},Y_{3},Y_{4},Y_{5} \right )$$
$Y_{i}$ 表示第 $i$ 次试验观察到的正反序列，注意这里的 $Y$ 代表随机变量序列，而不是代表随机变量。
将每次试验选择的是硬币 $A$ 还是硬币 $B$ 表示为
$$Z = \left ( Z_{1},Z_{2},Z_{3},Z_{4},Z_{5} \right )$$
$Z_{i} = A$ 表示选择硬币 $A$ 进行投掷；$Z_{i} = B$ 表示选择硬币 $B$ 进行投掷。$Z$ 也是表示一个随机变量序列。
对于第一种情况 $Z$ 是可以被观测到的，而第二种情况，$Z$ 无法被观测。
两种情况的似然函数为
$$L(\theta) = \ln P(Y | \theta) = \sum_{i = 1}^{n} \ln P(Y_{i} | \theta)$$
在这个抛硬币的问题中 $n = 5$。
1. 第一种情况
已知每个实验选择的是硬币 $A$ 还是硬币 $B$，通过试验得到若干样本，现在要计算输出的概率分布，可以直接求解似然函数。
$$L(\theta) = \sum_{i = 1}^{n} \ln P(Y_{i} | \theta) = \sum_{i = 1}^{5}\sum_{Z_{i}}^{} \ln P(Y_{i},Z_{i} | \theta) \\
= \sum_{i = 1}^{5}\bigg[ P(Z_{i} = A)\ln P(Y_{i} | Z_{i} = A,\theta) + P(Z_{i} = B)\ln P(Y_{i} | Z_{i} = B, \theta)\bigg] \\
= 0.5 \bigg [\ln \theta_{A}^{3}(1-\theta_{A})^{2} + \ln \theta_{B}^{2}(1-\theta_{B})^{3} + \ln \theta_{A}^{1}(1-\theta_{A})^{4} + \ln \theta_{B}^{3}(1-\theta_{B})^{2} + \ln \theta_{A}^{2}(1-\theta_{A})^{3} \bigg]$$
上面这个式子求导之后发现，$5$ 次实验中 $A$ 正面向上的次数再除以总次数作为即为 $\hat{\theta}_{A}$ ，$5$ 次实验中 $B$ 正面向上的次数再除以总次数作为即为 $\hat{\theta}_{B}$，即:
$$\hat{\theta}_{A} = \frac{6}{15} \\
\hat{\theta}_{B} = \frac{5}{10}$$
2. 第二种情况
由于每次实验并不知道选择的是硬币 $A$ 还是硬币 $B$，也就没有办法得到每个样本发生的概率，比如对于第一组试验，它发生的概率是 $\theta_{A}^{3}(1-\theta_{A})^{2}$ 呢？
还是 $\theta_{B}^{3}(1-\theta_{B})^{2}$ 呢？在这个情况里面，每次实验都多了一个隐藏变量 $Z_{i}$，这个变量 $Z_{i}$ 不知道，就无法去估计 $\theta_{A}$ 和 $\theta_{B}$，所以，我们必须先
估计出 $Z_{i}$，然后才能进一步估计 $\theta_{A}$ 和 $\theta_{B}$。
现在已经知道每次实验的结果了，如何计算在这个条件下，选择硬币 $A$ 的概率和选择硬币 $B$ 的概率呢？根据贝叶斯公式有：
$$P(Z_{i} = A | Y_{i}) = \frac{P(Z_{i} = A , Y_{i})}{P(Z_{i} = A , Y_{i}) + P(Z_{i} = B , Y_{i})} \\
P(Z_{i} = B | Y_{i}) = 1 - P(Z_{i} = A | Y_{i})$$
注意 $P(Z_{i} = A) = P(Z_{i} = B) = 0.5$ 的，而贝叶斯得到的是修正概率。那这其实也没办法算，比如对于
$$P(Z_{i} = A , Y_{i}) = P(Z_{i} = A)P(Y_{i} | Z_{i} = A) \\
= 0.5P(Y_{i} | Z_{i} = A) \\
= 0.5\theta_{A}^{Y_{i}}(1 - \theta_{A})^{5 - Y_{i}}$$
但是 $\theta_{A}$ 和 $\theta_{B}$ 却都不知道。我们可以先随机初始化一个 $\theta_{A}$ 和 $\theta_{B}$，用它来估计上面两个后验概率 $P(Z_{i} = A | Y_{i}), \; P(Z_{i} = B | Y_{i})$。
然后再按照极大似然估计法去估计新的 $\theta_{A}$ 和 $\theta_{B}$。回到这个抛硬币问题，我们先初始化 $\theta_{A} = 0.2,\theta_{B} = 0.7$，可计算出
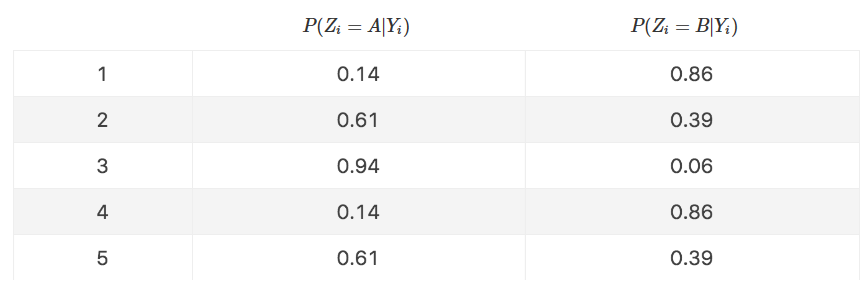
此时每一次优化的目标函数变了，将表格中的先验概率当作权重系数作用在原来的每一项上面，即
$$L(\theta) = \sum_{i = 1}^{5}\sum_{Z_{i}}^{} \ln P(Y_{i},Z_{i} | \theta) \; \Rightarrow \; L(\theta) = \sum_{i = 1}^{5}\sum_{Z_{i}}^{} \boldsymbol{P(Z_{i} | Y_{i})}\ln P(Y_{i},Z_{i} | \theta)$$
多了颜色加深的那部分系数，目标函数相当于期望求和，代入数据得：
$$L(\theta) = \sum_{i = 1}^{5}\sum_{Z_{i}}^{} \boldsymbol{P(Z_{i} | Y_{i})}\ln P(Y_{i},Z_{i} | \theta) \\
= \sum_{i = 1}^{5} \bigg[\boldsymbol{P(Z_{i} = A | Y_{i})} \cdot P(Z_{i} = A) \ln P(Y_{i} | Z_{i} = A,\theta) + \boldsymbol{P(Z_{i} = B | Y_{i})} \cdot P(Z_{i} = B)\ln P(Y_{i} | Z_{i} = B,\theta) \bigg ] \\
= 0.14 \cdot \ln \theta_{A}^{3}(1-\theta_{A})^{2} + 0.86 \cdot \ln \theta_{B}^{3}(1-\theta_{B})^{2} + \\
0.61 \cdot \ln \theta_{A}^{2}(1-\theta_{A})^{3} + 0.39 \cdot \ln \theta_{B}^{2}(1-\theta_{B})^{3} + \\
0.94 \cdot \ln \theta_{A}^{1}(1-\theta_{A})^{4} + 0.06 \cdot \ln \theta_{B}^{1}(1-\theta_{B})^{4} + \\
0.14 \cdot \ln \theta_{A}^{3}(1-\theta_{A})^{2} + 0.86 \cdot \ln \theta_{B}^{3}(1-\theta_{B})^{2} + \\
0.61 \cdot \ln \theta_{A}^{2}(1-\theta_{A})^{3} + 0.39 \cdot \ln \theta_{A}^{2}(1-\theta_{A})^{3} $$
上式整体少了个 $0.5$ 因子，但不影响最优解。函数 $L$ 对 $\theta_{A}$ 和 $\theta_{B}$ 求偏导，令导函数等于 $0$ 就可得到第一次迭代后的参数值。
这个过程就是 $EM$ 算法求解的思路。因为多了隐藏变量，所以没办法直接求解似然函数，$EM$ 算法是通过不断迭代一个带权重系数的函数来逼近原始问题
的解，重点是迭代的这个新的目标函数能不能代表原似然函数呢？下面进行推导。
$EM$ 算法推导
我们需要求解的似然函数为
$$L(\theta) = \sum_{i = 1}^{n} \ln \sum_{Z_{i}}^{}P(Y_{i},Z_{i} | \theta)$$
因为含有隐变量，上面这个式子是没有办法直接求出 $\theta$ 的。因此需要一些特殊的技巧：
$$L(\theta) = \sum_{i = 1}^{n} \ln \sum_{Z_{i}}^{}Q_{i}(Z_{i})\frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})}$$
上式引入了一个未知的新的分布 $Q_{i}(Z_{i})$，由于它是一个概率分布，所以满足
$$\sum_{Z_{i}}^{}Q_{i}(Z_{i}) = 1$$
根据 $Jensen$ 不等式得(因为 $\ln$ 是凸函数，所以不等式的不等号需要反一下)：
$$\ln \sum_{Z_{i}}^{}Q_{i}(Z_{i})\frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})} \geq \sum_{Z_{i}}^{}Q_{i}(Z_{i})\ln \frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})} $$
所以
$$L\left ( \theta \right ) \geq \sum_{i = 1}^{n}\sum_{Z_{i}}^{}Q_{i}(Z_{i})\ln \frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})} $$
现在我们想要找到一个 $Q_{i}(Z_{i})$ 的分布，使得上式等号成立。如果要满足 $Jensen$ 不等式的等号，则必须有：
$$\frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})} = c$$
其中 $c$ 是一个常数，将分母移到右边得
$$P(Y_{i},Z_{i} | \theta) = c \cdot Q_{i}(Z_{i}) \\
\Leftrightarrow \sum_{Z_{i}}^{}P(Y_{i},Z_{i} | \theta) = c \cdot \sum_{Z_{i}}^{}Q_{i}(Z_{i}) = c$$
所以
$$Q_{i}(Z_{i}) = \frac{P(Y_{i},Z_{i} | \theta)}{c} = \frac{P(Y_{i},Z_{i} | \theta)}{\sum_{Z_{i}}^{}P(Y_{i},Z_{i} | \theta)} \\
= \frac{P(Y_{i},Z_{i} | \theta)}{P(Y_{i} | \theta)} = P(Z_{i} | Y_{i},\theta)$$
也就是说当 $Q_{i}(Z_{i}) = P(Z_{i} | Y_{i},\theta)$ 时，不等式划等号，此时优化目标函数 $L(\theta)$ 就等价于优化下界，即
$$L(\theta) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}Q_{i}(Z_{i})\ln \frac{P(Y_{i},Z_{i} | \theta)}{Q_{i}(Z_{i})}$$
其中未知数只有 $\theta$，去掉上式中为常数的部分，则我们需要极大化的对数似然下界为：
$$L(\theta) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta)\ln P(Y_{i},Z_{i} | \theta) \;\;\;\;\;\;\;\;\;\;\;\; (2)$$
这和情况二每次迭代所求解的目标函数一模一样，后验概率作为权重系数，所以 $EM$ 算法是有严格的数学依据的。
$EM$ 算法的流程如下：
输入：观测数据 $Y = \left ( Y_{1},Y_{2},\cdots,Y_{n} \right )$，联合分布 $P(Y,Z|\theta)$，条件分布 $P(Z|Y,\theta)$，最大迭代次数 $J$。
1）随机初始化模型参数向量 $\theta$ 的初值 $\theta_{0}$。
2）$for \; j \; from \; 1 \; to \; J:$
a. $E$ 步：
$$Q_{i}(Z_{i}) := P(Z_{i} | Y_{i},\theta_{j}) \\
L(\theta) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}Q_{i}(Z_{i})\ln P(Y_{i},Z_{i} | \theta)$$
其中，$Q_{i}(Z_{i})$ 已经通过 $\theta_{j}$ 算出来了，是已知的，所以 $L(\theta)$ 只有未知数 $\theta$。
b. $M$ 步：极大化 $L(\theta)$ ,得到 $\theta$
$$\theta_{j+1} := arg \; \max_{\theta} \sum_{i = 1}^{n}\sum_{Z_{i}}^{}Q_{i}(Z_{i})\ln P(Y_{i},Z_{i} | \theta)$$
c. 如果 $\theta_{j+1}$ 已收敛，则算法结束。否则继续回到步骤 $a$ 进行 $E$ 步迭代。
$EM$ 算法的收敛性
$EM$ 算法的流程并不复杂，但是还有两个问题需要我们思考：
1）$EM$ 算法能保证收敛吗？
2）$EM$ 算法如果收敛，那么能保证收敛到全局最大值吗？
要证明 $EM$ 算法收敛，则我们需要证明我们的原始对数似然函数的值在迭代的过程中一直在增大，即：
$$\sum_{i = 1}^{n} \ln P(Y_{i} | \theta_{j + 1}) \geq \sum_{i = 1}^{n} \ln P(Y_{i} | \theta_{j})$$
第 $j + 1$ 次迭代的目标函数为
$$L(\theta,\theta_{j}) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j})\ln P(Y_{i},Z_{i} | \theta)$$
令
$$H(\theta,\theta_{j}) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j})\ln P(Z_{i} | Y_{i},\theta)$$
上两式相减得到：
$$L(\theta,\theta_{j}) - H(\theta,\theta_{j}) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j})\left ( \ln \frac{P(Y_{i},Z_{i} | \theta)}{P(Z_{i} | Y_{i},\theta)} \right ) \\
= \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j}) \ln P(Y_{i} | \theta) \\
= \sum_{i = 1}^{n}\ln P(Y_{i} | \theta)$$
在上式中分别取 $\theta$ 为 $\theta_{j}$ 和 $\theta_{j+1}$，并相减得到：
$$\sum_{i = 1}^{n}\ln P(Y_{i} | \theta_{j+1}) - \sum_{i = 1}^{n}\ln P(Y_{i} | \theta_{j}) = \\
\bigg [ L(\theta_{j+1},\theta_{j}) - L(\theta_{j},\theta_{j}) \bigg ] - \bigg [ H(\theta_{j+1},\theta_{j}) - H(\theta_{j},\theta_{j}) \bigg ]$$
由于 $\theta_{j+1}$ 使得 $L(\theta,\theta_{j})$ 极大，因此有:
$$L(\theta_{j+1},\theta_{j}) \geq L(\theta_{j},\theta_{j})$$
而对于第二部分，我们有：
$$H(\theta_{j+1},\theta_{j}) - H(\theta_{j},\theta_{j}) = \sum_{i = 1}^{n}\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j})\ln \frac{P(Z_{i} | Y_{i},\theta_{j+1})}{P(Z_{i} | Y_{i},\theta_{j})} \\
\leq \sum_{i = 1}^{n}\ln \left [\sum_{Z_{i}}^{}P(Z_{i} | Y_{i},\theta_{j}) \frac{P(Z_{i} | Y_{i},\theta_{j+1})}{P(Z_{i} | Y_{i},\theta_{j})} \right ] = 0$$
