GSP 算法

1. 项集数据和序列数据

   首先我们看看项集数据和序列数据有什么不同，如下图所示：

       

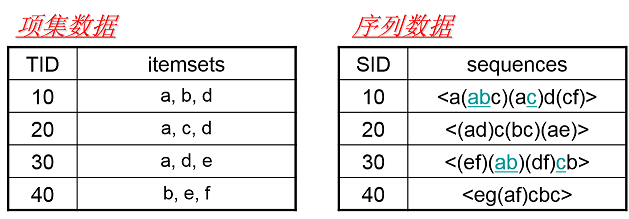
   左边的数据集是项集数据，在 Apriori 和 FP Tree 算法中已经看到过，每个项集数据由若干项组成，这些项没有时间上的先后关系。

   而右边的序列数据则不一样，它是由若干数据项集组成的序列。比如第一个序列 <a(abc)(ac)d(cf)>，它由 a,abc,ac,d,cf 共 5 个项

   集数据组成，并且这些项有时间上的先后关系。对于多于一个项的项集我们要加上括号，以便和其他的项集分开。同时由于项集内部是

   不区分先后顺序的，为了方便数据处理，我们一般将序列数据内所有的项集内部按字母顺序排序。

 

2. 子序列与频繁序列

   设序列 $A = \left \{ a_{1},a_{2},\cdots,a_{n} \right \}$，序列 $B = \left \{ b_{1},b_{2},\cdots,b_{m} \right \}$，且 $n \leq m$，如果存在数字序列 $1 \leq j_{1} \leq j_{2} \leq \cdots \leq j_{n} \leq m$ 满足

$$a_{1} \subseteq b_{j_{1}}, \; a_{2} \subseteq b_{j_{2}}, \cdots , \; a_{n} \subseteq b_{j_{n}}$$

   则称 $A$ 是 $B$ 的子序列，$B$ 是 $A$ 的超序列。

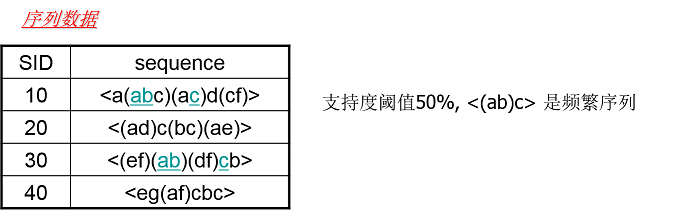
   频繁序列则和频繁项集类似，也就是频繁出现的子序列。比如对于下图，支持度阈值定义为 50%，也就是需要出现两次的子序列才是频繁序列。

   对于子序列 <(ab)c> 是频繁序列，因为它是图中的第一条数据和第三条序列数据的子序列，对应的位置用蓝色标示。

       

 

3. GSP(Generalized Sequential Pattern) 算法思想

   GSP 算法类似于 Apriori 算法，即如果一个子序列是不频繁的，那它所有的超序列都是不频繁的。算法步骤如下：

       1）扫描序列数据库，得到长度为 $1$ 的序列模式 $L_{1}$，作为初始的种子集。

       2）根据长度为 $i$ 的种子集 $L_{i}$ ，通过连接操作生成长度为 $i+1$ 的候选序列模式 $C_{i + 1}$；然后扫描序列数据库，计算每

          个候选序列模式的支持度，产生长度为 $i+1$ 的序列模式 $L_{i + 1}$，并将 $L_{i + 1}$ 作为新的种子集。

       3）重复第二步，直到没有新的序列模式或新的候选序列模式产生为止。

   举个例子，数据库中的数据如下图，每行都是一个序列数据：

            

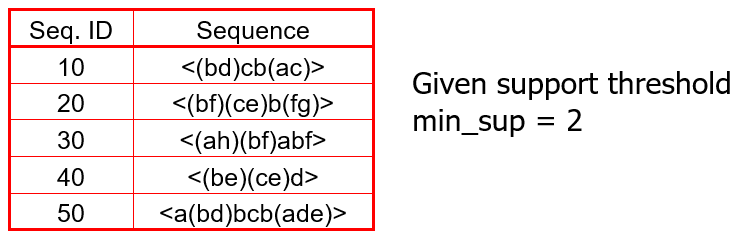
   计算 $5$ 个数据 $<a>, <b>,<c>,<d>,<e>,<f>,<g>,<h>$ 的支持度，比如 $<a>$ 是序列 $10,30,50$ 的子序列，所以它的支

   持度为 $3$，统计生成候选频繁 $1$ 项集 $C_{1}$，因为 $<g>,<h>$ 的支持度低于阈值，所以删掉，如上右图。

   接下来进行连接生成候选频繁 $2$ 项集 $C_{2}$，这里的连接和 Apriori 有点区别，因为两个相同的事件，如果顺序不同那就是不同的序列。

   $1$ 项集连接存在两种序列，一种是每个序列有 $2$ 个事件，如下左图；另一种是每个序列有 $1$ 个事件，如下右图。

             

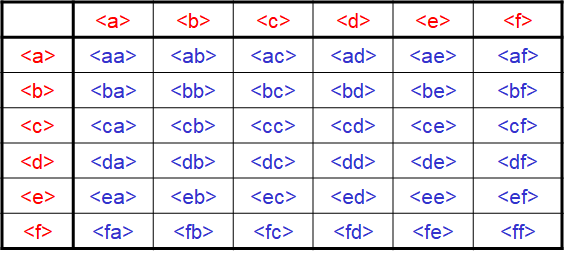
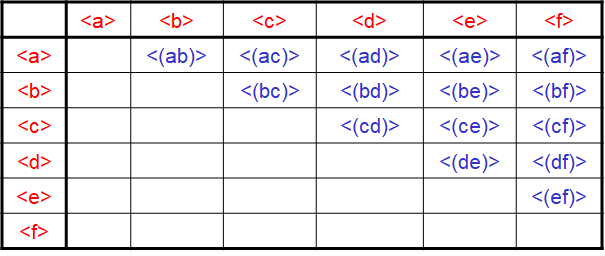
   再次扫描数据库得到 $36 + 15 = 51$ 个序列的支持度，删掉低于阈值的部分得到最终的频繁二项集 $L_{2}$。依次类推产生频繁 $3$ 项集，频繁 $4$ 项集。。。