正弦定理

先来看一个直角三角形，如下左图：

               

$\sin A$ 的值与三角形的边长有什么联系呢？

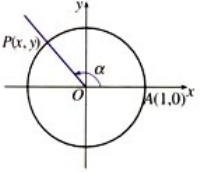
从右图可以看出，角 $\alpha$ 的正弦对应单位圆上点的纵坐标，如果不理解可以先去阅读博客。

现在要求角 $A$ 的正弦，应该以点 $A$ 为圆心做单位圆，以边 $AC$ 为 $x$ 轴，那么有

$$\sin A = y$$

根据比例关系得

$$\frac{y}{a} = \frac{1}{c}$$

所以

$$\sin A = y = \frac{a}{c}$$

可以这么理解：假如 $c = 1$，那么边 $CB$ 的长度 $a$ 直接就是角 $A$ 的正弦值，但是 $c \neq 1$，所以需要做一个归一化，即 $\frac{a}{c}$。

将形式变化一下：

$$\frac{a}{\sin A} = c$$

所以这个比值就是代表比例 $c$。现在不再是直角三角形了，换成任意一个三角形，如下左图：

               

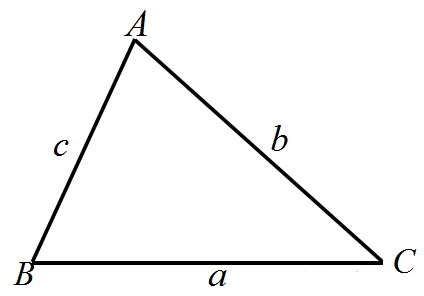
此时角 $A$ 的对边 $a$，和角 $A$ 的正弦比值代表什么含义呢？

$$\frac{a}{\sin A} = ?$$

画出三角形的外接圆，如下图

           

 

易知 $\angle A = \angle D$，所以

$$\frac{a}{\sin A} = \frac{a}{\sin D}$$

$\bigtriangleup ABC$ 虽然不是一个直角三角形，但是 $\bigtriangleup BCD$ 是一个直角三角形，根据直角三角形的结论

$$\frac{a}{\sin A} = \frac{a}{\sin D} = 2R$$

所以

$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$$

其中，$R$ 为三角形外接圆的半径。