集成学习之 AdaBoost 算法
集成学习简介
集成学习(ensemble learning)是现在非常火爆的机器学习方法。它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器(例如
同种算法但是参数不同,或者不同算法)来完成学习任务,也就是“博采众长”。一般会获得比任意单个学习器都要好的性能,尤其是在这些学习器
都是"弱学习器"的时候提升效果会很明显。
弱学习器:指的是性能不太好的学习器,比如一个准确率略微超过 50% 的二分类器。
按照每个学习器之间是否存在依赖关系可以将集成学习分为两类:
1)学习器之间存在强依赖关系,一系列基学习器需要串行生成,代表算法是 $Boosting$;
2)学习器之间不存在强依赖关系,一系列基学习器可并行生成,代表算法是 $Bagging$ 和随机森林。
$Boosting$ 指的是一类集成方法,即提升方法,其主要思想就是将弱的机器学习器提升($boost$)为强学习器。具体步骤如下:
1)先用每个样本权重相等的训练集训练一个初始的学习器;
2)根据上轮得到的学习器对训练集的预测表现情况调整训练集中的样本权重(例如提高被错分类的样本的权重使之在下轮训练中得到更多的关注),
然后据此训练出一个新的学习器;
3)重复 $2$ 直到得到 $M$ 个学习器,最终的集成结果是 $M$ 个学习器的组合。
由此看出,$Boosting$ 算法是一个串行的过程。$Boosting$ 算法簇中最著名的就是 $AdaBoost$,下面详细进行介绍。
$AdaBoost$ 算法
考虑如下形式的二分类(标准 $AdaBoost$ 算法只适用于二分类任务)训练数据集:
$$T = \left \{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\right \}$$
$x_{i}$ 是一个维度为 $d$ 的向量,$y_{i} \in \left \{ +1, -1 \right \}$。算法具体步骤如下:
1)初始化样本的权重:
$$D_{1} = \left \{ w_{11},w_{12},\cdots,w_{1n} \right \}$$
训练集有 $n$ 个样本,所以初始化了 $n$ 个权重,设置了权重的训练集也称为加权训练集,初始时每个样本设置的权重相等,均为 $w_{1i} = \frac{1}{n},i = 1,2,...,n$。
这里的样本权重是概率分布,即它们的和 $\sum_{i = 1}^{n}w_{1i} = 1$。
2)对 $m = 1,2,...,M$,重复以下操作得到 $M$ 个学习器:
a. 按照样本权重分布 $D_{m}$ 训练数据得到第 $m$ 个基本学习器 $G_{m}(x)$。
b. 计算 $G_{m}$ 在加权训练集上的分类误差率:
$$e_{m} = \sum_{i = 1}^{n}w_{mi}I \big ( G_{m}(x_{i}) \neq y_{i} \big )$$
$I$ 代表的是指示函数,它的含义是:当输入为 $True$ 的时候,输出为 $1$ ,输入为 $False$ 的时候,输出为 $0$。所以式子中,当学习器
输出的类别和实际的类别不一致时,指示函数值为 $1$。所以上面式子的含义就是:错误分类的样本对应的权重累加。考虑更加周全的
$AdaBoost$ 算法在这一步还应该判断是否满足基本条件(例如生成的基学习器是否比随机猜测好), 如果不满足,则当前基本学习器被抛弃,
学习过程提前终止。
c. 计算 $G_{m}$ 的系数(即最终集成使用的的基本学习器的权重):
$$\alpha_{m} = \frac{1}{2}\ln \frac{1 - e_{m}}{e_{m}}$$
为什么这样计算弱学习器权重系数?从上式可以看出,如果分类误差率 $e_{m}$ 越大,则对应的弱分类器权重系数 $\alpha_{m}$ 越小。也就是说,误
差率小的弱分类器权重系数越大。当 $e_{m} < 0.5$ 时,$\alpha_{m} > 0$;当 $e_{m} > 0.5$ 时,$\alpha_{m} < 0$。这里的 $\alpha_{m}$ 一定是正的,即分类误差率 $e_{m} < 0.5$,
如果 $e_{m} > 0.5$,那就把该分类器分类的结果都取一个相反的结果,这样一来取反后的分类器误差率还是小于 $0.5$。
d. 更新训练数据集的权值分布:
$$D_{m + 1} = \left ( w_{m+1,1},w_{m+1,2},\cdots,w_{m+1,n} \right ) \\
w_{m+1,i} = \frac{w_{mi}e^{-\alpha_{m}y_{i}G_{m}(x_{i})}}{Z_m}$$
$Z_{m}$ 是规范化因子,目的是为了使 $D_{m+1}$ 的所有元素和为 $1$,这样 $D_{m + 1}$ 才会成为一个概率分布。
$$Z_{m} = \sum_{i = 1}^{n}w_{mi}e^{-\alpha_{m}y_{i}G_{m}(x_{i})}$$
从 $w_{m+1,i}$ 计算公式可以看出,如果第 $i$ 个样本分类错误,则 $y_{i}G_{m}(x_{i}) < 0$,导致该样本的权重在第 $m+1$ 个弱分类器中增大,如果
分类正确,则权重在第 $m+1$ 个弱分类器中减少.至于样本权重更新公式为什么长这个样子,下面再解释。
$Z_{m}$ 与分类器 $G_{m}$ 的系数 $\alpha_{m}$ 有关,而 $\alpha_{m}$ 又与误差率 $e_{m}$ 有关,下面做个变形:
$$Z_{m} = \sum_{i = 1}^{n}w_{mi}e^{-\alpha_{m}y_{i}G_{m}(x_{i})} \\
= \sum_{y_{i} = G_{m}(x_{i})}^{}w_{mi}e^{-\alpha_{m}} + \sum_{y_{i} \neq G_{m}(x_{i})}^{}w_{mi}e^{\alpha_{m}} \\
= (1 - e_{m})e^{-\alpha_{m}} + e_{m}e^{\alpha_{m}} \\
= 2\sqrt{e_{m}(1 - e_{m})}$$
3)构建最终的分类器线性组合:
$$f(x) = \sum_{m = 1}^{M}\alpha_{m}G_{m}(x)$$
使用加权表决法得到最终的分类器为
$$G(x) = sgn\left (f(x)\right ) = sgn\left (\sum_{m = 1}^{M}\alpha_{m}G_{m}(x) \right )$$
由式子可以看出,最终的结果取决于权重大的分类器。
a. $\alpha_{m}G_{m}(x) > 0$:代表表决器投票结果为正类,绝对值越大代表发言权越大。
b. $\alpha_{m}G_{m}(x) < 0$:代表表决器投票结果为负类,绝对值越大代表发言权越大。
$AdaBoost$ 算法解释
上面介绍了分类 $Adaboost$ 的弱学习器权重系数公式和样本权重更新公式,但这些公式为什么长那个样子呢?其实它们可以从 $Adaboost$ 的损失函数推导出来。
1. 前向分步算法
$AdaBoost$ 算法最终得到的强分类器是若干个弱分类器加权求和而得到的,即
$$f(x) = \sum_{m = 1}^{M}\alpha_{m}G_{m}(x)$$
这是一个加性模型。我们希望这个模型在训练集上的经验误差最小,即
$$\min \sum_{i = 1}^{n}L \left ( y_{i}, f(x_{i}) \right ) \; \Leftrightarrow \; \min \sum_{i = 1}^{n}L \left ( y_{i}, \sum_{m = 1}^{M}\alpha_{m}G_{m}(x_{i}) \right )$$
通常这是一个复杂的优化问题。前向分步算法求解这一优化问题的思想就是:因为最终模型是一个加性模型,如果能从前往后,每一步只学习一个基本
学习器 $G_{m}(x)$ 及其权重 $\alpha_{m}$,不断迭代得到最终的模型,那么就可以简化问题复杂度。具体的,当我们经过 $m-1$ 轮迭代得到了最优模型 $f_{m-1}(x)$时,因为
$$f_{m}(x) = f_{m - 1}(x) + \alpha_{m}G_{m}(x)$$
优化目标就为
$$\min \sum_{i = 1}^{n}L\left ( y_{i}, f_{m - 1}(x_{i}) + \alpha_{m}G_{m}(x_{i}) \right )$$
求解上式即可得到第 $m$ 个基本分类器 $G_{m}(x)$ 及其权重 $\alpha_{m}$。
那么 $L$ 到底是个什么函数,它以样本正确输出类别 $y_{i}$ 和 $f_{m}(x_{i})$ 作为参数。
因为指数损失函数有更好的数学性质,例如处处可微,所以我们用它替代 $0/1$ 损失作为优化目标,目标函数为
$$L = \sum_{i = 1}^{n}e^{-y_{i}\left [ f_{m - 1}(x_{i}) + \alpha_{m}G_{m}(x_{i}) \right ]} \\
= \sum_{i = 1}^{n}e^{-y_{i}f_{m-1}(x_{i})} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
= \sum_{i = 1}^{n}\bar{w}_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})}$$
其中,$\bar{w}_{mi} = e^{-y_{i}f_{m-1}(x_{i})}$,我们的目的是希望求出当这个式子取最小值时对应的参数 $\alpha_{m},G_{m}(x)$,在求基学习器 $G_{m}(x)$ 时,它的前 $m - 1$ 个学习器
都已经知道,即 $f_{m - 1}(x) = \sum_{i = 1}^{m - 1}\alpha_{i}G_{i}(x)$ 是已知的。现在将式子 $L$ 继续做一个变形:
$$L = \sum_{i = 1}^{n}\bar{w}_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
= \sum_{y_{i} = G_{m}(x_{i})}^{} \bar{w}_{mi} \cdot e^{-\alpha_{m}} + \sum_{y_{i} \neq G_{m}(x_{i})}^{} \bar{w}_{mi} \cdot e^{\alpha_{m}} \\
= \left (\sum_{i = 1}^{n}\bar{w}_{mi} \cdot e^{-\alpha_{m}} - \sum_{y_{i} \neq G_{m}(x_{i})}^{} \bar{w}_{mi} \cdot e^{-\alpha_{m}} \right ) + \sum_{y_{i} \neq G_{m}(x_{i})}^{} \bar{w}_{mi} \cdot e^{\alpha_{m}} \\
= e^{-\alpha_{m}}\sum_{i = 1}^{n}\bar{w}_{mi} + \left ( e^{\alpha_{m}} - e^{-\alpha_{m}} \right )\sum_{i = 1}^{n}\bar{w}_{mi}I\left ( y_{i} \neq G_{m}(x_{i}) \right )$$
求这个函数的最小值分为两个阶段:
1)如下图,因为红色部分的系数为正,红色部分本身也为正,所以当红色的那一块取最小值时,函数 $L$ 的值会变小。
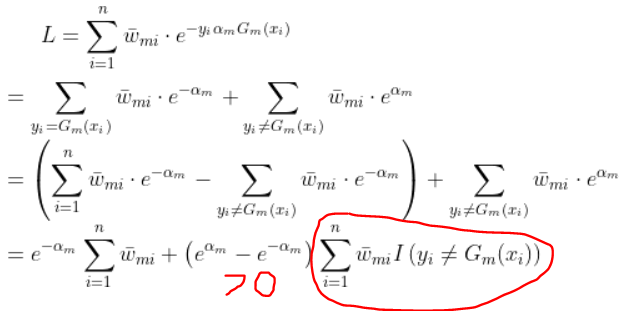
所以有
$$\hat{G}_{m}(x) = arg \; \min_{G_{m}(x)} \sum_{i = 1}^{n}\bar{w}_{mi}I\left ( y_{i} \neq G_{m}(x_{i}) \right )$$
现在已经得到了第 $m$ 个学习器的最优解,还需要求对应的权重系数 $\alpha_{m}$,$L$ 对 $\alpha_{m}$ 求导得
$$\frac{\partial L}{\partial \alpha} = -e^{-\alpha_{m}}\sum_{i = 1}^{n}\bar{w}_{mi} + \left ( e^{\alpha_{m}} + e^{-\alpha_{m}} \right )\sum_{i = 1}^{n}\bar{w}_{mi}I\left ( y_{i} \neq G_{m}(x_{i}) \right )$$
令这个式子等于 $0$,可解得
$$\hat{\alpha}_{m} = \frac{1}{2}\ln \frac{1 - e_{m}}{e_{m}}$$
其中
$$e_{m} = \frac{\sum_{i = 1}^{n}\bar{w}_{mi}I\left ( y_{i} \neq G_{m}(x_{i}) \right )}{\sum_{i = 1}^{n}\bar{w}_{mi}}$$
令 $w_{mi}$ 是 $\bar{w}_{mi}$ 归一化后的结果,即
$$w_{mi} = \frac{\bar{w}_{mi}}{\sum_{j = 1}^{n}\bar{w}_{mj}}$$
那么
$$e_{m} = \sum_{i = 1}^{n}w_{mi}I\left ( y_{i} \neq G_{m}(x_{i}) \right )$$
下面来看看 $\bar{w}_{mi}$ 和 $\bar{w}_{m+1,i}$ 之间的关系:
$$\bar{w}_{mi} = e^{-y_{i}f_{m-1}(x_{i})} \\
\bar{w}_{m+1,i} = e^{-y_{i}f_{m}(x_{i})} = e^{-y_{i}\left ( f_{m-1}(x_{i}) + \alpha_{m}G_{m}(x_{i}) \right )} \\
= e^{-y_{i}f_{m-1}(x_{i})} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
= \bar{w}_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})}$$
这个式子长得很像样本权重更新公式,在求 $\alpha_{m},G_{m}(x)$ 时,$w_{mi}$ 是已知的,令
$$C_{m} = \sum_{i = 1}^{n}\bar{w}_{mi}$$
$C_{m}$ 就是一个常数,函数 $L$ 除以任意常数不会影响最优解,因为 $w_{mi} = \frac{\bar{w}_{mi}}{C_{m}}$所以:
$$L = \sum_{i = 1}^{n}\bar{w}_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
\Leftrightarrow L = \sum_{i = 1}^{n}w_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})}$$
根据系数更新公式有
$$\bar{w}_{m+1,i} = \bar{w}_{mi} \cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
\Rightarrow C_{m+1}w_{m+1,i} = C_{m}w_{mi}\cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})} \\
\Rightarrow w_{m+1,i} = \frac{C_{m}}{C_{m+1}}w_{mi}\cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})}$$
因为常数不影响最优解,所以直接令
$$w_{m+1,i} = w_{mi}\cdot e^{-y_{i}\alpha_{m}G_{m}(x_{i})}$$
这就是 $adaboost$ 的样本权重更新公式。


