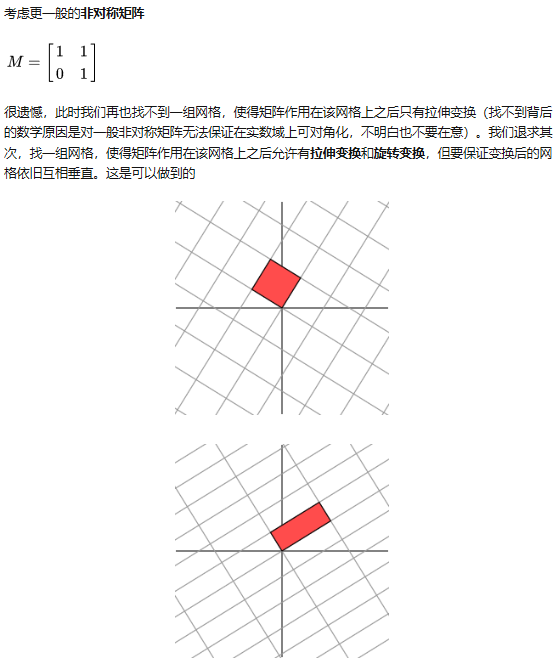
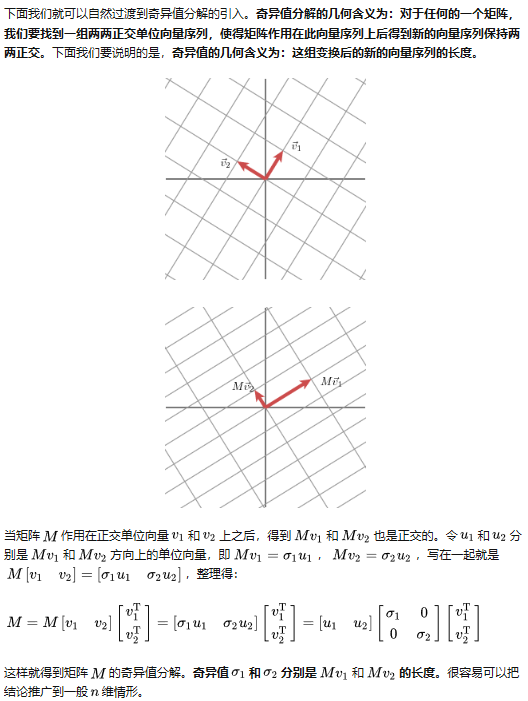
奇异值分解(SVD)
$\bullet$ 特征值分解。
特征值分解是针对方阵的,而且这个方阵必须能够相似对角化(如果不了解可以先去阅读一下矩阵相似的博客),那么就有
$$P^{-1}AP = \Lambda \; \Rightarrow \; A = P\Lambda P^{-1}$$
其中 $P$ 由特征向量构成,$\Lambda$ 由对应特征值构成的对角矩阵。
进一步得,当 $A$ 为实对称矩阵的时候,即 $A = A^{T}$,那么它可以被分解成如下的形式
$$A = P\Lambda P^{T}$$
其中,$P$ 为单位正交矩阵。
$\bullet$ 奇异值分解
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵。
奇异值分解基本定理:若 $A$ 为 $m \times n$ 实矩阵,则 $A$ 的奇异值分解存在
$$A = U \Sigma V^{T}$$
其中,$U$ 是 $m$ 阶单位正交矩阵,称左奇异矩阵,里面的向量称左奇异向量;$V$ 是 $n$ 阶单位正交矩阵,称右奇异矩阵,里面的向量称右奇异向量;
$\Sigma$ 是 $m \times n$ 矩形对角矩阵,其对角线元素非负(半正定),且按降序排列。可以发现,$A$ 和 $\Sigma$ 是同型矩阵。
下面看看怎么得到矩阵 $U,\Sigma,V$。
$$AA^{T} = U \Sigma V^{T}V\Sigma^{T}U^{T} = U \Sigma\Sigma^{T}U^{T} \\
A^{T}A = V\Sigma^{T}U^{T}U \Sigma V^{T} = V\Sigma^{T}\Sigma V^{T}$$
其中,$AA^{T}$ 是 $m$ 阶实对称矩阵,$A^{T}A$ 是 $n$ 阶实对称矩阵,$\Sigma \Sigma ^{T}$ 是 $m$ 阶方阵,$\Sigma ^{T} \Sigma$ 是 $n$ 阶方阵。
1)$A^{T}A$ 的特征值均为非负。令 $\lambda$ 是 $A^{T}A$ 的一个特征值,$\alpha$ 是对应的特征向量,则
$$A^{T}A\alpha = \lambda \alpha \\
\Rightarrow ||A\alpha||^{2} = (A\alpha)^{T}(A\alpha) = \alpha^{T}A^{T}A\alpha = \alpha^{T}\lambda \alpha = \lambda ||\alpha ||^{2} \\
\Rightarrow \lambda \geq 0$$
2)$A^{T}A$ 和 $AA^{T}$ 拥有相同的非零特征值,并且保持相同重数,并且属于非零特征值的特征向量间存在制约关系。
a. 首先证明方程 $Ax = 0$ 和 $A^{T}Ax = 0$ 同解。
如果 $Ax=0$,则 $A^{T}(Ax)=0$,所以 $Ax=0$ 的解为 $A^{T}Ax=0$ 的解。
对于 $A^{T}Ax=0$,两边同时乘以 $x^{T}$ ,得到 $x^{T}A^{T}Ax=0$。则有 $(Ax)^{T}(Ax)=0$,即 $||Ax||=0$。所以得到 $Ax=0$。
所以,$A^{T}Ax=0$ 的解都为 $Ax=0$ 的解。
所以 $Ax=0$ 和 $A^{T}Ax=0$ 有相同的解空间。所以 $r(A) = r(A^{T}A)$,同理有,$r(A^{T}) = r(AA^{T})$,于是有:
$$r(AA^{T}) = r(A^{T}) = r(A) = r(A^{T}A)$$
b. 证明:$A^{T}A$ 和 $AA^{T}$ 拥有相同的非零特征值,且特征向量间存在制约关系。
假设 $x$ 是 $A^{T}A$ 的特征值 $\lambda$ 所对应的特征向量,则有
$$A^{T}Ax = \lambda x$$
将上式两边左乘一个矩阵 $A$ 有
$$AA^{T}\left (Ax \right ) = \lambda \left (Ax \right )$$
那当 $x \neq 0$ 时,$Ax$ 是否也是非 $0$ 向量呢?
因为 $Ax = 0$ 和 $A^{T}Ax = 0$ 同解,所以要证明 $Ax \neq 0$,只需要证明 $A^{T}Ax \neq 0$,因为
$$A^{T}Ax = \lambda x \neq 0 \; \Rightarrow \; Ax \neq 0$$
c. 证明非 $0$ 特征值有相同的重数
$$\begin{bmatrix}
E_{n} & O \\
-A & E_{m}
\end{bmatrix}
\begin{bmatrix}
E_{n} & A^{T} \\
A & E_{m}
\end{bmatrix} =
\begin{bmatrix}
E_{n} & A^{T} \\
O & E_{m} - AA^{T}
\end{bmatrix}$$
$$\begin{bmatrix}
E_{n} & A^{T} \\
A & E_{m}
\end{bmatrix}
\begin{bmatrix}
E_{n} & O \\
-A & E_{m}
\end{bmatrix} =
\begin{bmatrix}
E_{n} - A^{T}A & A^{T} \\
O & E_{m}
\end{bmatrix}$$
上面两端取行列式有
$$|E_{m} - AA^{T}| = |E_{n} - A^{T}A|$$
于是
$$\left |\lambda E_{m} - AA^{T} \right | = \left |\lambda \left (E_{m} - \frac{1}{\lambda}AA^{T} \right )\right |$$
$$= \lambda^{m} \left |E_{m} - \frac{1}{\lambda}AA^{T} \right | \\
= \lambda^{m} \left |E_{m} - \left (\frac{1}{\lambda}A \right )A^{T} \right | \\
= \lambda^{m} \left |E_{n} - A^{T} \left (\frac{1}{\lambda}A \right ) \right | \\
= \lambda^{m - n} \lambda^{n}\left |E_{n} - A^{T} \left (\frac{1}{\lambda}A \right ) \right | \\
= \lambda^{m - n} \left |\lambda E_{n} - A^{T}A \right |$$
所以当特征值不为 $0$ 的时候,$AA^{T}$ 和 $A^{T}A$ 的特征多项式同解,即非零特征值重数相同。
现在对矩阵 $A^{T}A$ 进行特征值分解,求出全部的特征值和特征向量,将特征向量进行正交化和单位化,得到 $(v_{1}, v_{2},\cdots, v_{k})$。
设 $r(A^{T}A) = k$,将求出来的 $k$ 个非 $0$ 特征值按降序排列,特征值 $\lambda_{i}$ 对应的特征向量为 $v_{i}$,即
$$\lambda_{1} \geq \lambda_{2} \geq \cdots \geq \lambda_{k} \\
(v_{1}, v_{2},\cdots, v_{k})$$
由上面分析可知,矩阵 $AA^{T}$ 对应的非 $0$ 特征值也为 $\lambda_{i},i=1,2,...,k$,对应的特征向量为
$$(Av_{1}, Av_{2},\cdots, Av_{k})$$
对任意两个向量做内积得
$$A^{T}Av_{j} = \lambda_{j}v_{j} \\
\Rightarrow Av_{i} \cdot Av_{j} = (Av_{i})^{T}Av_{j} = v_{i}^{T}A^{T}Av_{j} = \lambda_{j} v_{i} \cdot v_{j} = 0$$
所以,因为 $v_{i},v_{j}$ 正交,所以任意两个不同向量 $Av_{i}$ 和 $Av_{j}$ 也正交。
现在只需要将其单位化即可,因为
$$A^{T}Av_{i} = \lambda_{i}v_{i} \\
\Rightarrow ||Av_{i}||^{2} = Av_{i} \cdot Av_{i} = (Av_{i})^{T}Av_{i} = v_{i}^{T}A^{T}Av_{i} = \lambda_{i} \\
\Rightarrow ||Av_{i}|| = \sqrt{\lambda_{i}}$$
所以矩阵 $AA^{T}$ 的 $k$ 个非 $0$ 特征值对应的单位且正交的特征向量组为
$$(\frac{1}{\sqrt{\lambda_{1}}}Av_{1}, \frac{1}{\sqrt{\lambda_{2}}}Av_{2},\cdots, \frac{1}{\sqrt{\lambda_{k}}}Av_{k})$$
所以
$$u_{i} = \frac{1}{\sqrt{\lambda_{i}}}Av_{i}, i = 1,2,...,k$$
奇异值为
$$\sigma_{i} = \sqrt{\lambda_{i}}, i = 1,2,...,k$$
所以,将矩阵 $A$ 奇异值分解的最终形式为
$$A = \begin{bmatrix}
u_{1} & u_{2} & \cdots & u_{k}
\end{bmatrix}_{m \times k}
\begin{bmatrix}
\sigma_{1} & & & \\
& \sigma_{2} & & \\
& & \ddots & \\
& & & \sigma_{k}
\end{bmatrix}_{k \times k}
\begin{bmatrix}
v_{1}^{T} \\
v_{2}^{T} \\
\vdots \\
v_{k}^{T}
\end{bmatrix}_{k \times n} \\
= \sigma_{1}u_{1}v_{1}^{T} + \sigma_{1}u_{2}v_{2}^{T} + \cdots + \sigma_{1}u_{k}v_{k}^{T}$$
可见,奇异值为 $0$ 的那些没必要考虑。
$\sigma$ 的值减少特别的快,为了节省可见,我们可以保留奇异值较大的若干项,舍去奇异值较小的项。这也是做 SVD 的意义。
奇异值往往对应着矩阵中隐含的重要信息,且重要性和矩阵的大小成正相关,每个矩阵 $A$ 都可以表示为一系列秩为 $1$ 的“小矩阵”之和,
而奇异值则衡量了这些“小矩阵”对于 $A$ 的权重。
下面,我们将奇异值/特征值,奇异向量/特征向量做一个对比。