SVM 之非线性支持向量机
支持向量机是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。
模型包括以下几类:
-
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
-
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
-
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
- 序列最小最优化算法 $SMO$;
1. 核函数
支持向量机通过某非线性变换 $\phi(x)$,将输入空间映射到高维特征空间。举一个例子:设输入空间是二维的,在该空间中取两个向量
$$v_{1} = (x_{1}, y_{1}) \\
v_{2} = (x_{2}, y_{2})$$
假如映射关系为
$$\phi(x,y) = \left ( x^{2}, \sqrt{2}xy, y^{2} \right )$$
函数的输入是二维的向量,输出是三维向量,也就是说这个函数完成了一个升维的操作。
$$\left (x_{1},y_{1} \right ) \; \overset{\phi(x,y)}{\rightarrow} \; \left ( x_{1}^{2}, \sqrt{2}x_{1}y_{1}, y_{1}^{2} \right ) \\
\left (x_{2},y_{2} \right ) \; \overset{\phi(x,y)}{\rightarrow} \; \left ( x_{2}^{2}, \sqrt{2}x_{2}y_{2}, y_{2}^{2} \right )$$
如果我们用神经网络来描述这个映射,网络结构可以长成下面这个样子:
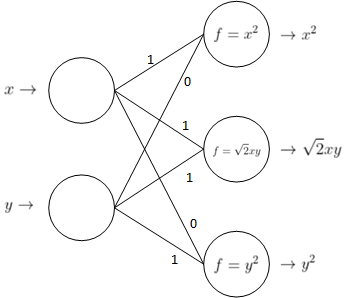
在这个网络中,输入层是 $2$ 维的,输出层是 $3$ 维的。神经网络也具有非线性拟合能力,其拟合能力显然高于非线性 $SVM$。
但是一般情况下这个映射函数是非常复杂的,很难写出它的具体表达式,它们映射到的高维空间的维数也比上面举的例子(三维)高得多,
甚至是无穷维的。于是引入核函数 $K(v_{1},v_{2})$,它是我们给定的,它的自变量是原始输入空间的向量。规定核函数必须满足条件:
$$K(v_{1}, v_{2}) = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle$$
$\phi(v_{1}), \phi(v_{2})$ 是 $v_{1},v_{2}$ 映射到高维空间后对应的向量,即规定核函数等于向量映射到高维空间后的内积,这个等式隐含着一个从低维空间
到高维空间的映射关系 $\phi$,一般解不出来且满足条件的映射不唯一。
对于最初的例子,给定核函数为 $K(v_{1},v_{2}) = \left \langle v_{1},v_{2} \right \rangle^{2}$,那么它满足如下等式
$$\left \langle v_{1},v_{2} \right \rangle^{2} = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle \\
\Rightarrow x_{1}y_{1} + x_{2}y_{2} = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle$$
映射到三维空间的可能解有:
1)$\phi(x,y) = \left ( x^{2}, \sqrt{2}xy, y^{2} \right )$
2)$\phi(x,y) = \frac{1}{\sqrt{2}}\left ( x^{2} - y^{2}, 2xy, x^{2} + y^{2} \right )$
2. 正定核
这些核函数是如何找到的?亦或者给定一个函数,有什么方法可以判定其是否可作为核函数?按 $1$ 中讲的,对于一个核函数 $K(v_{1},v_{2})$,
假如我们能找到一个映射 $\phi(x)$,使得
$$K(v_{1}, v_{2}) = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle$$
但上面也说了,这个映射函数很不好找,那么还有没有其它的办法判断一个给定的函数能不能作为核函数?
正定核的充要条件:
1)函数 $K(v_{1},v_{2})$ 是对称函数,即
$$K(v_{1},v_{2}) = K(v_{2},v_{1})$$
2)对于输入空间中的任意 $m$ 个向量 $x_{i},i = 1,2,...,m$,其对应的 $Gram$ 矩阵是半正定的。$Gram$ 矩阵定义为
$$K = \big[ K(x_{i},x_{j}) \big]_{m \times m}$$
给定的函数如果满足上面两个条件,那么它就可以作为核函数。这是另外一个判定核函数的方法。也就是说,我们按照这个充要条件构造
出来的函数必定也是满足核函数基本要求的,即:
$K(v_{1}, v_{2}) = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle$ $\Leftrightarrow$ $Gram$ 矩阵半正定且 $K$ 满足对称性。
下面我们将证明这个结论。
1)先证明从左到右成立:假设已知了 $K(v_{1}, v_{2}) = \left \langle \phi(v_{1}), \phi(v_{2}) \right \rangle$,因为是求内积,所以对称性是显而易见的。那么我们怎么推导
出 $Gram$ 矩阵半正定呢?根据半正定的定义,任选一个 $m$ 维非 $0$ 向量 $c$(这个向量和输入空间是没有关系的)有
$$c^{T}Kc = \begin{bmatrix}
c^{(1)} & c^{(2)} & \cdots & c^{(m)}
\end{bmatrix}\begin{bmatrix}
K_{11} & K_{12} & \cdots & K_{1m} \\
K_{21} & K_{22} & \cdots & K_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
K_{m1} & K_{m2} & \cdots & K_{mm}
\end{bmatrix}\begin{bmatrix}
c^{(1)} \\
c^{(2)} \\
\vdots \\
c^{(m)}
\end{bmatrix} \\
= \sum_{i = 1}^{m}\sum_{j = 1}^{m}c^{(i)}c^{(j)}K_{ij}
= \sum_{i = 1}^{m}\sum_{j = 1}^{m}c^{(i)}c^{(j)}\phi(x_{i})^{T}\phi(x_{j}) \\
= \sum_{i = 1}^{m}c^{(i)}\phi(x_{i})^{T} \sum_{j = 1}^{m}c^{(j)}\phi(x_{j}) \\
= \left (\sum_{i = 1}^{m}c^{(i)}\phi(x_{i}) \right )^{T} \left (\sum_{j = 1}^{m}c^{(j)}\phi(x_{j}) \right ) \\
= \left \langle \sum_{i = 1}^{m}c^{(i)}\phi(x_{i}), \sum_{j = 1}^{m}c^{(j)}\phi(x_{j}) \right \rangle \\
= \left \| \sum_{i = 1}^{m}c^{(i)}\phi(x_{i}) \right \|^{2} \geq 0$$
2)证明从右往左成立:反推暂时不太会,将来补上。
3. 核技巧在支持向量机中的应用
用线性分类方法求解非线性分类问题分为两步:首先使用一个变换将原空间的数据映射到新空间;然后再新空间里用线性分类学习方法从训练数据中学习
分类模型。求解线性可分问题的目标函数为
$$L(\alpha) = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i}^{T}x_{j}) -\sum_{i=1}^{n}\alpha_{i}$$
此时 $x_{i},x_{j}$ 都是经过映射后的高维空间中的向量,要在这个新的高维空间中求解出一个超平面,使样本点被正确分类。
观察式子可知,$x_{i}^{T}x_{j}$ 就等于核函数,所以目标函数可以写成如下形式
$$L(\alpha) = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}K(x_{i},x_{j}) -\sum_{i=1}^{n}\alpha_{i}$$
所谓核技巧,就是指我们可以直接计算 $K(x_{i},x_{j})$(核函数 $K$ 是已知的,根据充要条件可以构造),而不需要真正的去找一个 $\phi(x)$(通常是很难找的)。
也就是说,我们并不关心低维到高维的映射 $\phi$ 是什么样子的,我们只需要构造一个函数 $K$,使得该函数可以表示为映射后空间里数据的内积,这样就可以了。
求解出来的超平面也是位于高维空间的。


