SVM 之线性可分支持向量机
支持向量机是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。
模型包括以下几类:
-
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
-
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
-
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
- 序列最小最优化算法 $SMO$;
1. 基本概念
线性可分支持向量机前提:训练集样本线性可分。设训练集样本 $T$:
$$T = \left \{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\right \}$$
任意一个超平面 $(w,b)$ 关于样本点 $(x_{i},y_{i})$ 的几何间隔为:
$$\gamma_{i} = \frac{|w^{T}x_{i} + b|}{||w||} = \frac{y_{i}(w^{T}x_{i} + b)}{||w||}$$
这里的几何间隔不是指点到超平面的距离,而是实例点到超平面带符号的距离,可以为负数,此时样本点被错误分类;当样本点被正确分类时,
几何间隔才等于点到超平面的距离。
任意一个超平面关于训练集 $T$ 的几何间隔定义为:所有样本点到超平面几何间隔的最小值,即
$$\gamma = \min_{i}\gamma_{i} = \min_{i} \frac{y_{i}(w^{T}x_{i} + b)}{||w||}$$
那么这个到超平面距离最小的样本点就称为这条直线的支持向量。举个例子,观察下图
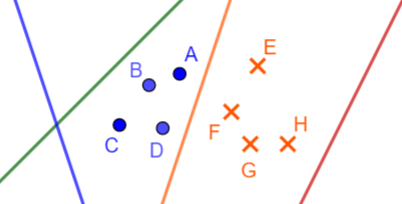
对于同一个超平面 $(w,b)$,【错误分类点的几何间隔 $< 0 <$ 正确分类点的几何间隔】
1)绿色直线的支持向量为点 $D$,几何间隔为 $\gamma_{i} \bigg |_{D}$,是一个负数。
2)蓝色直线的支持向量为点 $A$,几何间隔为 $\gamma_{i} \bigg |_{A}$,也是一个负数。
3)橙色直线的支持向量为点 $A \; or \; D$,几何间隔为 $\gamma_{i} \bigg |_{A}$,是一个正数,等于距离。
并不是每一个样本点都可以成为支持向量,比如图中的 $H$ 点,就没办法找到一条直线,使它到该直线的几何间隔比其它样本点的都小。
支持向量的个数取决于样本,一般是有限的几个,且位于边界。
每个支持向量都会对应一簇超平面,这簇超平面到该支持向量的几何间隔比其它样本点都小。
2. 什么样的超平面才是最优超平面?
考虑如下左图 $1$,过点 $I$ 和点 $F$ 做两条平行线,且平行线之间没有其它的样本点,那么位于这两条平行线之间的直线必然是要么以 $I$ 点为
支持向量,要么以 $F$ 点为支持向量。现在我们将这两条直线同步地逆时针旋转,旋转过程中必须保持两条平行线之间没有其它样本点,旋转到
一定程度,如下图 $2$。此时达到临界点,如果在两条平行线之间选择一条分割线,显然黑线会是最好的。
如果在 $C$ 和 $F$ 两点做平行线,如下图 $3$,很明显图 $3$ 中的平行线之间的间隔更大,那么能否认为 $3$ 中的黑色直线比 $2$ 中的更优?
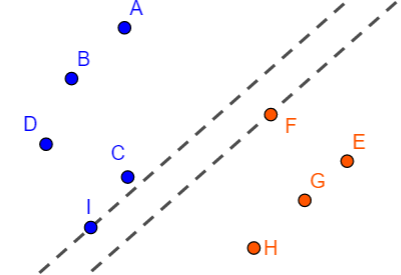
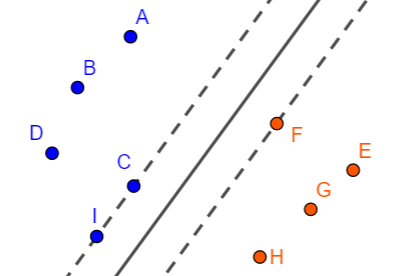
上图中的虚线称为支撑超平面,很明显正类和负类都各有一个支撑超平面,它们一一对应,即满足:
1)每一个支撑超平面都经过支持向量,且相互平行。
2)两个支撑超平面之间没有其它样本点,是一个“真空”区域。
硬间隔:两个对应的支撑超平面之间的距离。
线性可分支持向量机模型选择的依据是:硬间隔最大化。也就是说当两个支撑超平面之间的距离最大的时候,位于它们中间的那个超平面就是最优超平面。
按这种思路,图 $3$ 中的黑线是优于图 $2$ 的。
3. 建立约束最优化问题
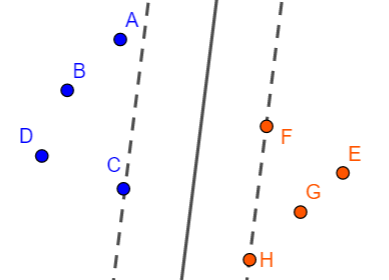
仍然以 $2$ 中的图为例。先只考虑假设空间中的超平面,即会使样本点都被正确分类的超平面,这些超平面只会位于下图所示位置:
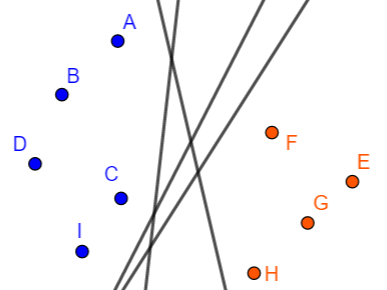
图中 $A,C,I,F,H$ 都可能成为分离超平面的支持向量,我们目标是:求出一组参数 $w,b$ 使得对应的硬间隔最大。
现在需要确定一个指标来作为评判标准。
观察一下 $2$ 中的图 $2$,黑色直线到点 $I$ 或点 $F$ 的距离是最大的,此时它的支持向量有两个,即点 $I,F$,这是一个临界直线,往左,
则支持向量仅为 $I$;往右,则支持向量仅为 $F$。
而我们要求的那个黑色直线满足:所有以点 $I$ 或点 $F$ 为支持向量的直线簇中,与支持向量的几何间隔最大的那条。
另外,做为支持向量的点只需要考虑正类或者负类,因为一方会决定另一方。求解步骤如下:
1)设点 $H$ 坐标 $(x_{H},y_{H})$,则该点到超平面 $(w,b)$ 的几何间隔为
$$\gamma_{H} = \frac{y_{H}\left ( w^{T}x_{H} + b\right )}{||w||}$$
则几何间隔最大的那个超平面为
$$(w,b) = arg \max_{w,b} \; \gamma_{H}$$
求解过程中必须保证支持向量仍然为 $F$,即其它样本点到超平面的距离都必须 $\geq \gamma_{H}$,于是有 $n$ 个约束:
$$\frac{y_{i}\left ( w^{T}x_{i} + b\right )}{||w||} \geq \gamma_{H}, \; i = 1,2,\cdots,n$$
2)设点 $F$ 坐标 $(x_{F},y_{F})$,与 1)中过程相同,可得到:
$$\gamma_{F} = \frac{y_{F}\left ( w^{T}x_{F} + b\right )}{||w||} \\
(w,b) = arg \max_{w,b} \; \gamma_{F} \\
s.t. \;\;\; \frac{y_{i}\left ( w^{T}x_{i} + b\right )}{||w||} \geq \gamma_{F}, \; i = 1,2,\cdots,n$$
上面两步之后会得到 $2$ 条分割线,取几何间隔最大的那条作为最终的分离超平面。
但是,上面的求解过程是站在了上帝视角,给了一堆样本点,我们根本就不会知道哪些点能作为支持向量,即 $H,F$ 点都是未知的。
我们来观察一下 $\gamma_{H}$,思考一个问题:分子的取值会不会影响最优化问题的解?
分析:对于超平面 $w^{T}x + b = 0$,可以按比例改变系数 $w,b$,改变后仍然代表同一个超平面,设点 $x_{0}$,那么它到这个超平面的距离为 $d = \frac{|w^{T}x + b|}{|w|}$,
现在调整 $w,b$ 为 $\lambda w,\lambda b$,距离 $d$ 恒定不变,但分子和分母都各自改变了,也就是说,可以通过调整比例 $\lambda$ 使分子出现任何数值,那么总会存在
一个比例 $\lambda_{0}$ 使得
$$|\;(\lambda_{0} w)^{T}x + \lambda_{0}b\;| = 1 \\
w \rightarrow w^{'} = \lambda_{0}w \\
b \rightarrow b^{'} = \lambda_{0}b$$
此时距离公式变成 $d = \frac{1}{|w^{'}|}$。
现在来考虑 $\gamma_{H}$,最优化问题是求它的最大值,设最优解为 $(w^{*},b^{*})$,备选的直线是:所有以点 $H$ 为支持向量的直线簇(约束),那么这些
直线也可以各自调整它们的系数 $w,b$,调整后仍然会代表相同的直线。也就是说,每一条直线都会存在一个系数 $\lambda$,使得调整后的参数 $w^{'},b^{'}$ 满足
$$y_{H}\left ( (w^{'})^{T}x_{H} + b^{'} \right ) = 1 \\
w^{'} = \lambda w \\
b^{'} = \lambda b$$
那么此时求得的最优解就变成了 $\left ( \lambda w^{*}, \lambda b^{*} \right )$,代表的仍然是同一个超平面。
此时惊讶的发现根本就没必要知道支持向量的具体数值,上面的步骤 1)和 2)就可以写到一起,如下:
$$max \; \frac{1}{||w||} \\
s.t. \;\;\; y_{i}\left ( w^{T}x_{i} + b\right ) \geq 1, \; i = 1,2,\cdots,n$$
上面就等价于求分母的最小值,于是得到最终所要求解的最优化问题
$$min \; \frac{1}{2}||w||^{2} \\
s.t. \;\;\; y_{i}\left ( w^{T}x_{i} + b\right ) - 1 \geq 0, \; i = 1,2,\cdots,n$$
为什么这么转化呢?可能与凸优化相关,暂时不论。
4. 最优超平面唯一性证明
只需要证明:以某个样本点作为支持向量的最优超平面唯一。
比如 $2$ 中的图,以点 $H$ 为支持向量的直线簇中,只能找到一条直线,它到点 $H$ 的几何间隔最大。
证明:
采用反证法。即假设存在两个几何间隔最大的超平面 $(w_{1}^{*}, b_{1}^{*}),(w_{2}^{*}, b_{2}^{*})$,因为都是最优解,所以:
$$||w_{1}^{*}|| = ||w_{2}^{*}|| = c$$
将这两个解代入约束条件有:
$$y_{i}(w_{1}^{*}x_{i} + b_{1}^{*}) - 1 \geq 0\\
y_{i}(w_{2}^{*}x_{i} + b_{2}^{*}) - 1 \geq 0$$
上面两式相加得:
$$y_{i}\left ( \frac{w_{1}^{*} + w_{2}^{*}}{2} \cdot x_{i} + \frac{b_{1}^{*} + b_{2}^{*}}{2}\right ) - 1 \geq 0$$
令 $w = \frac{w_{1}^{*} + w_{2}^{*}}{2}, \; b = \frac{b_{1}^{*} + b_{2}^{*}}{2}$,所以 $(w,b)$ 是问题的可行解(满足约束条件的解),根据向量三角不等式有
$$c \leq ||w|| = ||\frac{1}{2}w_{1}^{*} + \frac{1}{2}w_{2}^{*}|| \leq \frac{1}{2}||w_{1}^{*}|| + \frac{1}{2}||w_{2}^{*}|| = c$$
所以有
$$||w_{1}^{*} + w_{2}^{*}|| = ||w_{1}^{*}|| + ||w_{2}^{*}|| \\
\Rightarrow \; w_{1}^{*} = w_{2}^{*}$$
现在,最优解 $(w_{1}^{*}, b_{1}^{*}),(w_{2}^{*}, b_{2}^{*})$ 可以记为 $(w^{*}, b_{1}^{*}),(w^{*}, b_{2}^{*})$,下面证明它们的截距也相同。
对于超平面 $(w^{*}, b_{1}^{*})$,在正类和负类中分别选择一个它的支持向量 $x_{1}^{'},x_{1}^{''}$,则这两个向量会使约束条件取等号,即
$$w^{*}x_{1}^{'} + b_{1}^{*} - 1 = 0 \\
-w^{*}x_{1}^{''} - b_{1}^{*} - 1 = 0$$
对于超平面 $(w^{*}, b_{2}^{*})$,在正类和负类中分别选择一个它的支持向量 $x_{2}^{'},x_{2}^{''}$,则这两个向量会使约束条件取等号,即
$$w^{*}x_{2}^{'} + b_{1}^{*} - 1 = 0 \\
-w^{*}x_{2}^{''} - b_{1}^{*} - 1 = 0$$
分别得到
$$b_{1}^{*} = -\frac{1}{2}(w^{*}x_{1}^{'} + w^{*}x_{1}^{''}) \\
b_{2}^{*} = -\frac{1}{2}(w^{*}x_{2}^{'} + w^{*}x_{2}^{''}) \\
\Rightarrow \; b_{1}^{*} - b_{2}^{*} = -\frac{1}{2}\left [ w^{*} \cdot (x_{1}^{'} - x_{2}^{'}) + w^{*} \cdot (x_{1}^{''} - x_{2}^{''}) \right ]$$
又因为
$$w^{*}x_{2}^{'} + b_{1}^{*} \geq 1 = w^{*}x_{1}^{'} + b_{1}^{*} \\
w^{*}x_{1}^{'} + b_{2}^{*} \geq 1 = w^{*}x_{2}^{'} + b_{2}^{*} \\
\Rightarrow \; w^{*}(x_{1}^{'} - x_{2}^{'}) = 0$$
同理:$w^{*}(x_{1}^{''} - x_{2}^{''}) = 0$,所以 $b_{1}^{*} = b_{2}^{*}$。
证毕
5. 最优化问题求解
如果不懂什么是拉格朗日乘子和拉格朗日对偶,可先阅读这两篇博客。
现在要求解的原始问题为:
$$min \; \frac{1}{2}||w||^{2} \\
s.t. \;\;\; 1 - y_{i}\left ( w^{T}x_{i} + b\right ) \leq 0, \; i = 1,2,\cdots,n$$
定义拉格朗日函数:
$$L(w,b,\alpha) = \frac{1}{2}||w||^{2} + \sum_{i=1}^{n}\alpha_{i}\left [ 1 - y_{i}\left ( w^{T}x_{i} + b\right ) \right ]\\
= \frac{1}{2}||w||^{2} + \sum_{i=1}^{n}\alpha_{i}\left [ 1 - y_{i}\left ( w^{T}x_{i} + b\right ) \right ] \\
= \frac{1}{2}||w||^{2} - \sum_{i=1}^{n}\alpha_{i}y_{i}\left ( w^{T}x_{i} + b\right ) + \sum_{i=1}^{n}\alpha_{i}, \;\; \alpha_{i} \geq 0, \; i = 1,2,...,n$$
可以写出求解这个不等式约束问题的 KKT 条件:
$$\left\{\begin{matrix}
L_{w} = w - \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i} = 0 \\
L_{b} = -\sum_{i=1}^{n}\alpha_{i}y_{i} = 0 \\
y_{i}\left ( w^{T}x_{i} + b\right ) - 1 \geq 0, \; i = 1,2,\cdots,n \\
\alpha_{i} \left [ y_{i}\left ( w^{T}x_{i} + b\right ) - 1 \right ] = 0, \; i = 1,2,\cdots,n \\
\alpha_{i} \geq 0
\end{matrix}\right. \; \Rightarrow \;
\left\{\begin{matrix}
w = \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i} \\
\sum_{i=1}^{n}\alpha_{i}y_{i} = 0 \\
b = y_{j} - w^{T}x_{j} = y_{j} - \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i}^{T}x_{j}, \;(\alpha_{j} > 0)
\end{matrix}\right.$$
如果 $\alpha$ 的任何一个分量都为 $0$,则可推出法向量 $w$ 为 $0$,矛盾,所以必有一个分量 $\alpha_{j} > 0$,通过这个正分量来计算 $b$。
很明显:只要知道了 $\alpha_{i},\; i = 1,2,...,n$ 就能够求出 $w,b$。
$\bullet$ 下面采用拉格朗日对偶来求。
原始问题为
$$\min_{w,b} \bigg [ \max_{\alpha_{i} \;:\;\alpha_{i} \geq 0} L(w,b,\alpha) \bigg]$$
它对应的对偶问题为
$$\max_{\alpha_{i} \;:\;\alpha_{i} \geq 0} \bigg [ \min_{w,b} L(w,b,\alpha) \bigg]$$
1)求 $\min_{w,b} L(w,b,\alpha)$
$$\left\{\begin{matrix}
L_{w} = w - \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i} = 0\\
L_{b} = -\sum_{i=1}^{n}\alpha_{i}y_{i} = 0
\end{matrix}\right. \;\Rightarrow \;
\left\{\begin{matrix}
w = \sum_{i=1}^{n}\alpha_{i}y_{i}x_{i}\\
\sum_{i=1}^{n}\alpha_{i}y_{i} = 0
\end{matrix}\right.$$
将求解结果代入拉格朗日函数得
$$L(w,b,\alpha) = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j}) - \sum_{i=1}^{n}\alpha_{i}y_{i} \left [ \left (\sum_{j=1}^{n}\alpha_{j}y_{j}x_{j}^{T} \right )x_{i} + b\right ] + \sum_{i=1}^{n}\alpha_{i} \\
= -\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i}^{T}x_{j}) + \sum_{i=1}^{n}\alpha_{i}$$
2)求 $\min_{w,b} L(w,b,\alpha)$ 对 $\alpha$ 的极大
对偶的目的就是为了消去 $w,b$,将 1)中得到的结果添个负号改为极小化问题,如下:
$$\min_{\alpha } \; \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i}^{T}x_{j}) -\sum_{i=1}^{n}\alpha_{i} \\
s.t. \;\;\; \sum_{i=1}^{n}\alpha_{i}y_{i} = 0 \\
\alpha_{i} \geq 0, \; i = 1,2,\cdots,n$$
我们先看看这样化简有什么好处?
第一个好处就是未知数的个数下降了, 把前面含有 $w$ 和 $b$ 的未知数消去了,现在的未知数只剩下 $\alpha_{i}$ 和 $\alpha_{j}$,其他未知数都为已知量。
现在的问题是怎么求 $\alpha$。采用的是 $SMO$ 算法,将在另一篇博客介绍。


