数据分析之 Numpy 包
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
官方文档地址:https://numpy.org/doc/stable/index.html。
下面简述一些 Numpy 库常用方法和属性。
1. NumPy 支持的数据类型
尽管 Python 支持 int、float 等基础的数据类型,但是 NumPy 需要更多、更精确的数据类型支持科学计算以及内存分配的需要。
下面列举了一些固定大小的类型别名:
np.bool # 用一个字节存储的布尔类型(True或False), 可用字符 'b' 表示 np.int8 # 一个字节大小, -128 ~ 127, 可用字符串 'i1' 表示, 后面的 1 就表示 1 字节, 下面也一样 np.int16 # 整数, -32768 ~ 32767, 可用字符串 'i2' 表示 np.int32 # 整数, −2^31 ~ 2^32−1, 可用字符串 'i4' 表示 np.int64 # 整数, −2^63 ~ 2^63−1, 可用字符串 'i8' 表示 np.uint8 # 无符号整数, 0 ~ 255, 可用字符串 'u1' 表示 np.uint16 # 无符号整数, 0 ~ 65535, 可用字符串 'u2' 表示 np.uint32 # 无符号整数, 0 ~ 2^32−1, 可用字符串 'u4' 表示 np.uint64 # 无符号整数, 0 ~ 2^64−1, 可用字符串 'u8' 表示 np.float16 # 半精度浮点数: 16位,正负号1位, 指数5位, 精度10位, 可用字符串 'f2' 表示 np.float32 # 单精度浮点数: 32位,正负号1位, 指数8位, 精度23位, 可用字符串 'f4' 表示 np.float64 # 双精度浮点数: 64位,正负号1位, 指数11位, 精度52位, 可用字符串 'f8' 表示 np.complex64 # 复数, 分别用两个32位浮点数表示实部和虚部, 可用字符串 'c8' 表示 np.complex128 # 复数, 分别用两个64位浮点数表示实部和虚部, 可用字符串 'c16' 表示 np.object_ # python对象, 可用字符 'O' 表示 np.string_ # 字符串, 可用字符 S 表示(在S后面添加数字, 表示字符串长度, 比如 S3 表示长度为三的字符串, 不写则为最大长度) np.unicode_ # unicode类型, 可用字符 'U' 表示
这些类型在 NumPy 里属于元(原子性、不可分、最小单位)数据类型。
2. numpy.dtype() 方法
这个方法返回一个数据类型对象,仅用来描述 ndarray 数组中每个元素对应的内存区域如何使用,即 ndarray 数组元素的数据类型。
所以 ndarray 对象的属性中包含一个 numpy.dtype 类型的实例。方法原型如下:
""" object: 可以转换为数据类型的对象, 为 None 的话就是 float64 align: 如果为 true,填充字段使其类似 C 的结构体。 copy: 对参数 object 是深拷贝还是浅拷贝, """ numpy.dtype(object, align, copy)
那么哪些对象可以转化为 dtype 类型呢?
1)提供的 object 参数本身就是 dtype 类型。
2)为 None,那就代表 float64。
3)标量类型,包括 Python 内置的基础数据类型或者 numpy 内置的元数据类型。
dt = np.dtype(np.int16) dt = np.dtype(float)
4)python 的类类型
class test:
def __init__(self, s):
self.sstr = s
dt = np.dtype(test)
5)字符串,可以是 numpy 元数据类型的组合
dt = np.dtype('<f4') # 小端,单精度浮点数
dt = np.dtype('>i8') # 大端,长整型
6)元组列表,每个元组都具有以下形式:(字段名称、数据类型、形状),其中 Shape 是可选的
dt = np.dtype([('x', 'f4'), ('y', np.float32), ('z', 'f4', (2, 2))]) # 最后一个是 2*2 的 float 数组
dt = np.dtype([('name', str, 40), ('num_items', np.int32), ('price', np.float32)])
dt = np.dtype(('S10', 1))
3. NumPy Ndarray 对象
Numpy 库所操作的对象就是 ndarray,即多维数组,它是一系列同类型数据的集合。
多维数组:数组的数组。每一个维度都是一个数组,区别在于元素是矢量还是标量,如果元素是矢量,意味着这个维度的数组本身还是一个多维数组,
如果元素是标量,那么这个维度的数组就是一维数组。假设最外层的数组维度为 $1$,那么以 $3$ 维数组为例:
1)第 $1$ 维数组的每个元素是 $2$ 维数组,即确定一个参数便可得到一个 $2$ 维数组。
2)第 $2$ 维数组的每个元素是 $1$ 维数组,即确定两个参数便可得到一个 $1$ 维数组。
3)第 $3$ 维数组的每个元素是标量,总共确定三个参数后便得到最终的元素值。
维数:描述一个数学对象所需的参数个数。比如上面的 $3$ 维数组,取到最后的标量需要 $3$ 个参数。
ndarray 对象由两大部分组成:
1)原始数组数据(raw array data):也称为数据缓冲区,是包含固定大小数据项的连续(固定)内存块。
将 ndarray 与 python 中的 list 对比一下,list 可以容纳不同类型的对象,像 string、int、tuple 等都可以放在一个 list 里,
所以 list 中存放的是对象的引用,再通过引用找到具体的对象,这些对象所在的物理地址并不是连续的。
2)原始数组数据描述信息(metadata):这些信息可以包括如下内容,
a. 基本数据元素的大小(以字节为单位)。
b. 数据缓冲区中数据的起始位置。
c. 每个维度的元素之间的分隔(跨度)。
d. 数据的字节顺序。
e. 缓冲区是否为只读。
f. 有关基本数据元素解释的信息(通过 np.dtype 对象)。数据元素可以像 int 或 float 一样,也可以是复合对象(例如,类似于 struct 的对象)。
ndarray 的设计思路是数据存储与其解释方式分离,让尽可能多的操作发生在解释方式上,而尽量少操作实际存储数据的内存区域。
$\bullet$ metadata 都包含哪些信息呢?或者说 ndarry 对象有哪些属性呢?
ndarray.shape # 每个维度数组的元素数量-元组 ndarray.ndim # 数组的维数 ndarray.size # 数组中的标量元素数量,即最后一维数组的元素个数 ndarray.dtype # 数组元素的类型,是 np.dtype 实例对象,指示了每个数据占用多少个字节,这几个字节怎么解释,比如int32、float32等 ndarray.itemsize # 数组中元素的字节大小 ndarray.strides # 每个维度数组的元素大小(间隔)-元组
$\bullet$ 如何创建一个 ndarray 对象?
1)numpy.array():该方法创建一个 ndarray 数组对象,方法原型如下:
""" object: 可以转化为数组的对象, 即 array_like, 可以是列表、元组等 dtype : 可选, 数组元素的数据类型, 可以是任何可以转为数据类型(dtype)的对象 copy : 可选, 为 True 表示生成的 ndarray 对象由参数 object 对象深拷贝而来, 为 False, 则是浅拷贝 order : 指定阵列的内存布局, 'C'为按行方向, 'F'为列方向 subok : 默认返回一个与基类类型一致的数组 ndmin : 指定生成数组的最小维度 """ ndarrayObj = numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)
2)numpy.linspace():该方法用于创建一个一维数组,数组是一个等差数列构成的,原型如下:
""" start: 序列的起始值 stop: 序列的终止值,如果 endpoint 为 true, 该值包含于数列中 num: 要生成的等步长的样本数量, 默认为50 endpoint: 该值为 true 时,数列中包含 stop 值, 反之不包含, 默认是True retstep: 如果为 True 时, 生成的数组中会显示间距, 反之不显示 dtype: ndarray 的数据类型, 可以是任何可以转为 dtype 的类型, 默认为 None, 转为 dtype 后就是 float64 类型 """ ndarrayObj = numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
4. numpy 索引
有多种方法可以对数组元素进行索引,下面一一介绍。阅读本部分之前,最好先去了解下 python 对内置类型的切片索引语法。
1)数字索引:这种方式很简单,每个维度都可以指定一个数字来索引,每个维度索引结果的交集就是输出。举个例子:


观察上面左边这张图,红色框框是第一个维度的数字 $1$ 的索引结果,绿色框框是第二个维度的数字 $2$ 的索引结果,蓝色框框是第三个维度的数字 $3$
的索引结果,三个索引结果的交集就是 $33$。除了从交集角度来理解索引结果外,还可以这样理解:下一个维度的索引都是在上一个维度索引结果的基
础上进行的,也就是说,第一个维度确定了红色框框后,第二个维度的索引直接在 $arr[1]$ 上进行就可以了,第三个维度的索引在 $arr[1,2]$ 上进行。
上面的右图就是按第二种理解画出来的,用来索引的数字如果是负数,代表从右往左数,$-1$ 就是代表最后一个元素。
2)切片索引:python 对 numpy 的切片在语法上并没有什么特殊之处,和 python 对内置类型的切片语法一致,特殊之处在于:数组切片是原始数组视图,
这就意味着,如果做任何修改,原始数组也会跟着更改。如果不想更改原始数组,就需要进行显式的复制,从而得到它的副本(.copy())。
import torch
import numpy as np
a = np.arange(10)
b = a[3:6]
print("a =", a)
print("b =", b)
b[2] = 99
print("a =", a)
print("b =", b)
a[:2] = 101
print("a =", a)
"""
a = [0 1 2 3 4 5 6 7 8 9]
b = [3 4 5]
a = [ 0 1 2 3 4 99 6 7 8 9]
b = [ 3 4 99]
a = [101 101 2 3 4 99 6 7 8 9]
"""
下面举两个用切片索引多维数组的情况,理解方式和 1)中是一样的,即可以理解成是并行索引结果的交集或串行索引结果的递进。

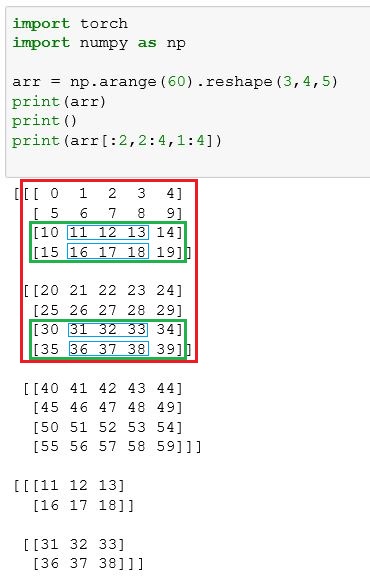
在上面左边这张图中,第一个维度和第二个维度都索引都是 $:$,这个是代表该维度的数据全选,如果不理解可先去看切片索引的博客。
最终的交集就是如上所示的二维矩阵。
3)布尔索引:我们可以通过一个布尔数组(numpy 数组)来索引目标数组,以此找出与布尔数组中值为 True 的对应的目标数组中的数据。需要注意的是:
布尔数组的长度必须与目标数组对应的轴的长度一致。
import torch
import numpy as np
arr = np.arange(6).reshape(1,2,3)
booling = np.array([[[True, False, True],
[False, True, True]]])
print(arr)
print(arr[booling]) # [0 2 4 5]
booling = np.array([[True, False]])
print(arr[booling]) # [[0 1 2]]
由上面的例子可知,想索引到维度 $3$,那么 booling 数组的形状就得是 $(1,2,3)$,想索引到维度 $2$,那么 booling 数组的形状为 $(1,2)$,
也就是:用来索引的布尔数组的形状必须和原数组的前缀形状相同,至于这个前缀形状是多大取决于索引到哪个维度。再看个例子:
import torch import numpy as np arr = (np.arange(36)).reshape(6,6) print(arr) print() x = np.array([0, 1, 2, 1, 4, 5]) booling = x == 1 # 通过比较运算得到一个布尔数组 print(booling) print(arr[booling]) print() print(arr[booling,2:]) """ [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23] [24 25 26 27 28 29] [30 31 32 33 34 35]] [False True False True False False] [[ 6 7 8 9 10 11] [18 19 20 21 22 23]] [[ 8 9 10 11] [20 21 22 23]] """
4)花式索引:利用整数数组(这里的数组,可以是 numpy 的数组,也可以是 python 自带的list )进行索引,其意义是根据索引数组的值作为目标数组
的某个轴的下标来取值。对于使用一维整型数组作为索引,如果目标是一维数组,那么索引的结果就是对应位置的元素;如果目标是二维数组,那么
就是对应下标的行。
import torch
import numpy as np
arr = np.empty((8,4))
for i in range(8):
arr[i] = i
print(arr)
print()
print(arr[[2,6,1,7]])
print()
print(arr[[-2,-6,-1]])
"""
[[0. 0. 0. 0.]
[1. 1. 1. 1.]
[2. 2. 2. 2.]
[3. 3. 3. 3.]
[4. 4. 4. 4.]
[5. 5. 5. 5.]
[6. 6. 6. 6.]
[7. 7. 7. 7.]]
[[2. 2. 2. 2.]
[6. 6. 6. 6.]
[1. 1. 1. 1.]
[7. 7. 7. 7.]]
[[6. 6. 6. 6.]
[2. 2. 2. 2.]
[7. 7. 7. 7.]]
"""
我们可以看到花式索引的结果,以一个特定的顺序排列。而这个顺序,就是我们所传入的整数列表或者 ndarray。这也为我们以特定的顺序来选取
数组子集,提供了思路。
一次传入多个索引数组,会返回一个一维数组,其中的元素对应各个索引元组。
import torch import numpy as np arr = np.arange(35).reshape(5,7) print(arr) print() print(arr[[1,3,2,4],[2,0,6,5]]) """ [[ 0 1 2 3 4 5 6] [ 7 8 9 10 11 12 13] [14 15 16 17 18 19 20] [21 22 23 24 25 26 27] [28 29 30 31 32 33 34]] [ 9 21 20 33] """
经过对比可以发现,返回的一维数组中的元素,分别对应 $(1,2),(3,0)....$,我们传入来两个索引数组,相当于传入了一组平面坐标,从而进行了定位。
照这样理解的话,那么对应一个 $N$ 维数组,如果传入 $N$ 个索引数组的话,就相当于传入了一个 $N$ 维坐标。
import torch import numpy as np arr = np.arange(27).reshape(3,3,3) print(arr) print() print(arr[[1,2],[0,1],[2,2]]) # (1,0,2), (2,1,2) """ [[[ 0 1 2] [ 3 4 5] [ 6 7 8]] [[ 9 10 11] [12 13 14] [15 16 17]] [[18 19 20] [21 22 23] [24 25 26]]] [11 23] """
将花式索引和切片索引结合,如
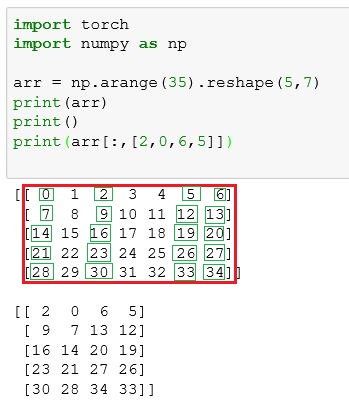
依然采用交集准则或者递推准则即可。
5. 一些常用的方法
1)np.pad:是用来是数组进行填充数的,函数原型如下:
""" array - 表示需要填充的数组 pad_width - 表示每个轴(axis)边缘需要填充的数值数目 mode - 为填补类型, 即怎样去填补 """ ndarray = numpy.pad(array, pad_width, mode, **kwargs)
上面这个原型解释的不是很清楚,直接来看个例子:
import numpy as np A = np.arange(95,99).reshape(2,2) A = np.pad(A, ((4,2),(2,5)), 'constant', constant_values = ((0,1),(4,3))) print(A) """ [[ 4 4 0 0 3 3 3 3 3] [ 4 4 0 0 3 3 3 3 3] [ 4 4 0 0 3 3 3 3 3] [ 4 4 0 0 3 3 3 3 3] [ 4 4 95 96 3 3 3 3 3] [ 4 4 97 98 3 3 3 3 3] [ 4 4 1 1 3 3 3 3 3] [ 4 4 1 1 3 3 3 3 3]] """


