牛顿法

阅读本篇之前，可先阅读一下梯度下降法。下面介绍一下牛顿法的基本思路。记原始的函数为 $F(x)$，它对应的二阶泰勒展开式为 $f(x)$

将目标函数 $F(x)$ 进行二阶泰勒展开(如果不了解这个可先阅读博客)得：

$$f(x) = f(x_{0}) + \nabla f(x_{0})^{T}(x - x_{0}) + \frac{1}{2}(x - x_{0})^{T}G(x_{0})(x - x_{0})$$

接下来对这个函数求一阶偏导数和二阶偏导数，如果不知道怎么求，可先阅读以下博客：向量内积求偏导、二次型求偏导、向量对向量求偏导。

函数 $f(x)$ 对列向量 $x$ 求偏导得

$$\nabla f(x) = \nabla f(x_{0}) + G(x_{0})(x - x_{0})$$

这个结果向量是由 $f(x)$ 对各坐标轴的偏导数组成。

将列向量 $\nabla f(x)$ 继续对 $x^{T}$ 求偏导，结果为

$$\nabla^{2} f(x) = G(x_{0})$$

这个结果矩阵由 $f(x)$ 的各个二阶偏导数组成，即海森矩阵，很明显它是一个与自变量无关的常矩阵。这就很神奇：原函数 $F(x )$在 $x_{0}$ 点

的海森矩阵居然就是泰勒展开式 $f(x)$ 在任一点处海森矩阵(因为是常矩阵，与变量无关了)。

我们知道某点是极值点的必要条件是其一阶偏导数为 $0$，即梯度向量为 $0$，令

$$\nabla f(x) = 0$$

这个方程并不一定有解，就算有解，解出来的就一定是局部极小值点吗？很显然不一定，所以牛顿法做了一个极强的假设：每个迭代点或泰勒展开点 $x_{k}$ 处，

矩阵 $G(x_{k})$ 正定。对于第一次迭代，因为 $G(x_{0})$ 正定，故矩阵可逆，所以可解得

$$x_{1} = x_{0} - G^{-1}(x_{0})\nabla f(x_{0})$$

那这个点是极小值点吗？因为 $G(x_{0})$ 是正定的，所以泰勒二阶展开式 $f(x)$ 的海森矩阵就是正定矩阵，所以必然存在极小值。

之后将一阶偏导数为 $0$ 的点 $x_{1}$ 作为下一次泰勒二阶展开点，继续求偏导数为 $0$ 的点 $x_{2}$，如此循环。。。

现在，我们来分析下这个新的点对应的函数值 $f(x_{1})$ 是否较原来的 $f(x_{0})$ 小？因为已经假设矩阵 $G(x_{0})$ 正定，所以有

$$- \nabla f(x_{0})^{T}G^{-1}(x_{0})\nabla f(x_{0}) < 0$$

说明向量 $- G^{-1}(x_{0})\nabla f(x_{0})$ 和梯度向量的夹角是一个钝角，所以在这个方向上函数值是减少的。

但是我们根本没有办法保证原函数 $f(x)$ 对每一次迭代点的海森矩阵都是正定的，即无法保证牛顿法的每一次迭代方向一定沿着函数值下降的方向。

所以，牛顿法不能保证迭代最终能够收敛。

    

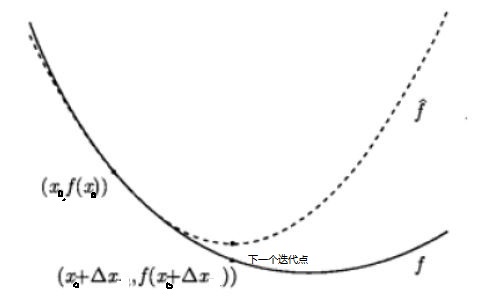
从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次

曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。