拉格朗日乘子法和 KKT 条件
在求解最优化问题中,拉格朗日乘子法和 KKT 条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法,在有不等约束时使用 KKT 条件。
1 无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于 $0$ 的点可能是极值点。将结果带回原函数进行验证即可。
2 等式约束条件(拉格朗日条件)
考虑约束最优化问题:
$$min \; f(x) \\
s.t. \;\;\; g_{i}(x) = 0 \;\;\; i = 1,2,\cdots, k$$
问题有 $k$ 个等式约束,$x$ 是一个 $n$ 维的向量,即 $x = (x^{(1)}, x^{(2)}, \cdots, x^{(n)})^{T}$。
如果我们想绘制函数 $f(x)$ 和 $g_{i}(x)$,那需要在 $n + 1$ 维空间,而绘制 $f(x) = C_{1}$ 和 $g_{i}(x) = C_{2}$ 需要在 $n$ 维空间。
1)关于等高(值)线
那么降一个维度后,图像 $f(x) = C_{1}$ 和 $g_{i}(x) = C_{2}$ 代表什么呢?
a. $f(x) = C_{1}$ 表示函数 $f(x)$ 的等高线,$C_{1}$ 可以取任意值,$n$ 维空间中的任意一个点都会有一条与之对应的等高线,在这条线上,函数值相同。
b. $g_{i}(x) = C_{2}$ 表示函数 $g_{i}(x)$ 的等高线,因为约束条件 $g_{i}(x) = 0$($C_{2} = 0$),所以每个约束函数只对应一条等高线。
在 $n$ 维空间中,设所有约束函数的等高线相交的图像为 $M$,我们的目标是在 $M$ 上找到函数 $f(x)$ 的局部极值。
注意:$M$ 上的任意一个点肯定都会对应一条 $f(x)$ 的等高线,推广到高维,这个等高线就是代表一个线性空间。
2)梯度向量和等值线的关系
理解了等高线(等值线),还需要知道某点的梯度方向和过这一点的等高线的关系。
多元函数中的方向导数指的是 $xoy$ 平面上的一个矢量,梯度方向代表所有方向中函数值增长最快的方向,我们知道等高线上所有点的函数值
都是相等的,所以某点的梯度方向必然不会是与等高线相切,那应该怎么移动呢?
先给出结论:梯度方向与等高线的切线方向垂直。
证明:
对于任意一条等高线 $f(x,y) = C$,其上任意一点的切线斜率为:
$$k = -\frac{f_{x}^{'}}{f_{y}^{'}}$$
所以该点的法线斜率为:
$$k^{'} = -\frac{1}{k} = \frac{f_{y}^{'}}{f_{x}^{'}}$$
又该点的梯度向量为:
$$(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})$$
梯度向量的斜率和法线向量的斜率是一样的,所以梯度方向和法线方向是一样的。
证毕
3)关于可行域
所有不等式约束和等式约束会有一个交集,交集可以是一个点,一个曲面或一个高维的线性空间,将这个交集称为可行域,
可行域内的点才满足约束条件,所以必须在可行域内考虑问题。
现在假设有 $k$ 个约束条件:$g_{1}(x),g_{2}(x),\cdots,g_{k}(x)$,它们的可行域为 $S$,在 $S$ 上取一点 $(x,y)$,那么各约束条件在该
点处的梯度 $\nabla g_{1}(x),\nabla g_{2}(x),\cdots, \nabla g_{k}(x)$ 和可行域方向有什么联系呢?
高维空间想象不出来,我们先考虑二维和三维(即约束条件是一元或二元函数),然后进行推广。
a. 当 $k = 1$ 时,那么约束条件本身就是可行域,在曲面或曲线上任一点的任意切线方向(即可行域方向)与该点的梯度必然相互垂直。
b. 当 $k = 2$ 时,且约束条件是 $2$ 个曲面,那么可行域就是它们的交线,交线上任意一点处的切线是两个约束曲面 $g_{1}(x),g_{2}(x)$在该点
处切平面的交线,而梯度 $\nabla g_{1}(x),\nabla g_{2}(x)$ 是各自切平面的法线,所以可行域方向会垂直于 $\nabla g_{1}(x),\nabla g_{2}(x)$。
所以:可行方向的全体是 $\nabla g_{1}(x),\nabla g_{2}(x),\cdots, \nabla g_{k}(x)$ 张成的线性子空间的正交子空间。
4)可行域内某点为极值的条件
我们先考虑二维和三维(即约束条件是一元或二元函数),然后进行推广。
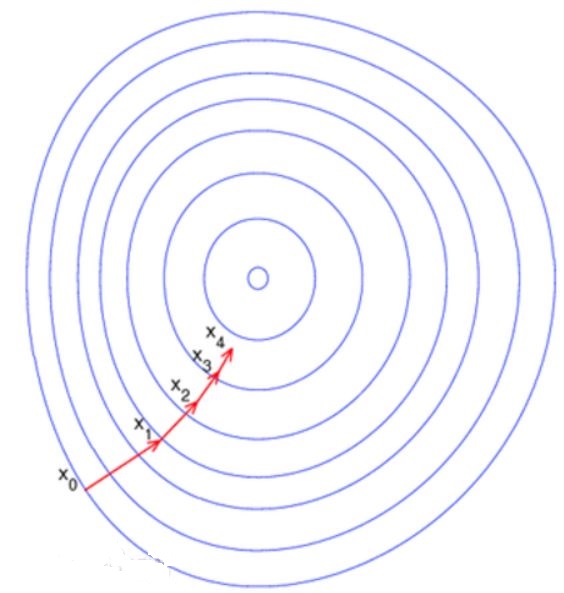
a. 首先来看一个例子:
$$max/min \; f(x,y) = x^{2} + y^{2}\\
s.t. \; x^{2}y = 3 $$

如上图所示,蓝线是约束,点只能在上面移动,红线是目标函数的等高线,有无数条。蓝线和红线一共就两种情况:
i:蓝线与红线相交
如图中 $C$ 点,这样的点会成为极值点吗?
因为是相交的,那么蓝线上的点便可以穿过红线,此时不妨假设目标函数 $f(x)$ 在点 $C$ 处的梯度向量朝外,如图中 $\nabla f$。
那么在这个相交点 $C$ 的邻域内,$C$ 点若移动到 $C_{1}$ 处,此时函数值便会增加,若向下移动到 $C_{2}$ 处,此时函数值
就会减少,所以 $C$ 点或者任一相交点不满足极值的条件,在相交点处,均可再继续移动来使函数值增大或者减小。
ii:蓝线与红线相切
如图中 $A,B$ 两点,这样的点会成为极值点吗?
在 $A$ 点的邻域内,$A$ 点到蓝线(邻域内)上的任意一点的方向必然与梯度向量的夹角均为锐角或钝角,对 $B$ 点也是如此,所以
在 $A$ 点或 $B$ 点处再移动点,只能导致函数值超一个方向变动,即只增大或只减少。
所以 $A$ 点和 $B$ 点都是约束条件下的极值点。
b. 下面再来看一个例子,如下图
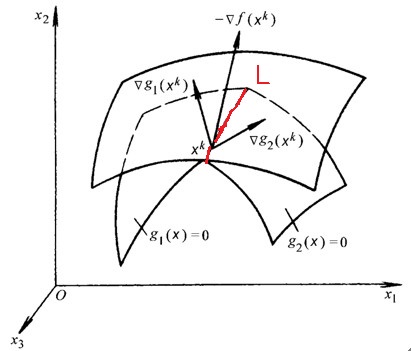
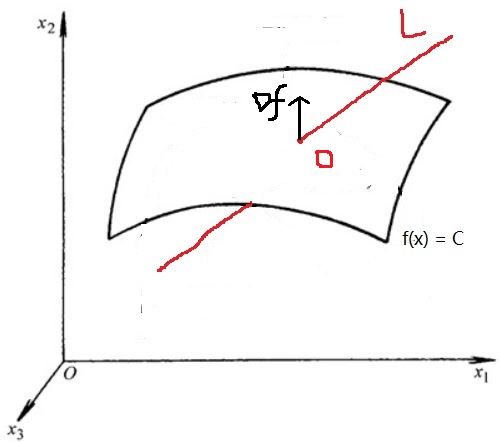
i:曲线 $L$ 和 $f(x)$ 的等高面相交
如上右图所示,和上面的分析类似,在 $O$ 点的邻域内,红线上的点可以继续向上或向下移动,向上移动则函数值继续增加(因为梯度方向
和切线方向夹角为锐角),向下移动则函数值会减少,所以交点不会是极值点。
ii:曲线 $L$ 和 $f(x)$ 的等高面相切
此处不再赘述,切点是极值点。
综上分析得:只有可行域和目标函数等高线相切的点才会是极值点,即可行域方向和目标函数的梯度方向互相垂直的点才会是极值点,
也可以说,某点的 $\nabla f(x)$ 必须落在对应的 $\nabla g_{1}(x),\nabla g_{2}(x),\cdots, \nabla g_{k}(x)$ 张成的线性子空间中(线性表示),该点才会成为极值点。
为求解极值点,可列方程:
$$\left\{\begin{matrix}
\nabla f = \lambda_{1} \nabla g_{1} + \lambda_{2} \nabla g_{2} + \cdots + \lambda_{k} \nabla g_{k} \\
g_{i} = C_{i}, \;\;\; i = 1,2,\cdots,k
\end{matrix}\right.$$
这样约束问题就变成了一个无约束问题,即下面两个问题是等价的:
$$\left\{\begin{matrix}
\min_{x} \; f(x) \\
s.t. \;\;\; g_{i}(x) = 0 \;\;\; i = 1,2,\cdots, k
\end{matrix}\right.
\; \Leftrightarrow \;
\min_{x,\lambda}L(x,\lambda) = f(x) + \sum_{i=1}^{k}\lambda_{i}g_{i}(x)$$
3 不等式约束条件(KKT条件)
考虑约束最优化问题:
$$min \; f(x) \\
s.t. \;\;\; g_{i}(x) \leq 0, \;\;\; i = 1,2,\cdots,k \\
c_{j}(x) = 0, \;\;\; j = 1,2,\cdots, l $$
问题有 $k$ 个等式约束和 $l$ 个不等式约束,$x$ 是一个 $n$ 维的向量,即 $x = (x^{(1)}, x^{(2)}, \cdots, x^{(n)})^{T}$。
上面的问题比较复杂,现在考虑简单一点的情形,即只有一个不等式约束:
$$min \; f(x) \\
s.t. \;\;\; g(x) \leq 0 $$
拉格朗日函数:
$$L(x,\lambda) = f(x) + \lambda g(x),\lambda \geq 0$$
那么就只有如下两种情形:
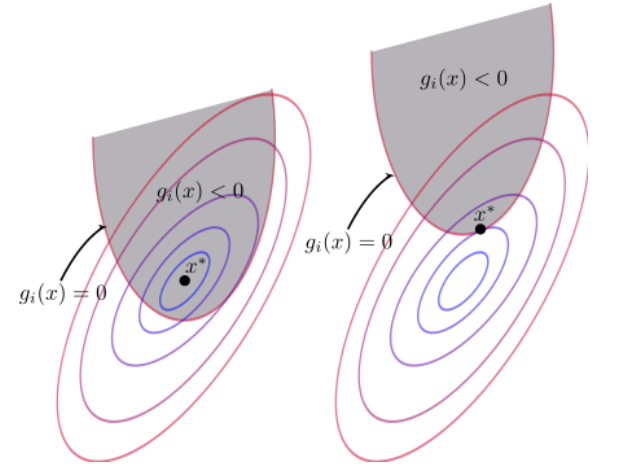
1)$f(x)$ 在约束条件下的极值点本身就在可行域里面(如上左图)
如果不是相切,那么对任意一个在可行域中的点,如果在它附近往里走或者往外走,$f(x)$ 一般都会变大或者变小,所以绝大部分点都不会是极值点。
除非这个点在可行域内部,且本身就是 $f(x)$ 的极值点。这样的话,不等式约束就失效了,直接求 $f(x)$ 的极小值点即可。求解方程为:
$$\left\{\begin{matrix}
\nabla f = 0\\
g(x) < 0 \\
\lambda = 0
\end{matrix}\right.$$
2)$f(x)$ 在约束条件下的极值点还是在 $g(x) = 0$ 边界曲线上(如上右图)
对于这种情况,不等式约束就变成等式约束了,这时就可以使用 $2$ 中介绍的方法,所求解的方程为:
$$\left\{\begin{matrix}
\nabla f + \lambda g = 0\\
g(x) = 0 \\
\lambda \geq 0
\end{matrix}\right.$$
下面解释下为什么 $\lambda \geq 0$。
图中阴影部分是可行域,边界上的点 $x^{*}$ 为最终所求的极值点,讨论如下两个梯度方向:
a. 约束函数 $g(x)$ 在点 $x_{*}$ 处的梯度方向:因为阴影部分 $g(x) < 0$,那个方向的函数值更小,所以 $g(x)$ 的梯度是指向大于 0 的一侧,
也就是不是可行域的一侧。
b. 目标函数 $f(x)$ 在点 $x_{*}$ 处的梯度方向:因为已经假定极值点发生在边界曲线上,且所求的问题是极小值,如果 $\nabla f$ 指向非阴影区域,
那么意味着梯度反方向指向可行域,那显然还可以继续往可行域移动找到函数值更小的点,所以 $f(x)$ 的梯度指向可行域的一侧。
因为极值点处 $\nabla f$ 和 $\nabla g$ 梯度方向相反,所以必须 $\lambda \leq 0$(可以为 $0$,意味着该点就是 $f(x)$ 的极小值点)。
综上可得求解方程组:
$$\left\{\begin{matrix}
\nabla f + \lambda g = 0\\
g(x) \leq 0 \\
\lambda \geq 0 \\
\lambda g(x) = 0
\end{matrix}\right.$$
这个方程组就是该问题的 KKT 条件,只有满足这些条件才会存在极小值。
回到最初的问题,它的 KKT 条件为:
$$\left\{\begin{matrix}
\min_{x} \; f(x) \\
s.t. \;\; g_{i}(x) \leq 0, \;\;\; i = 1,2,\cdots,k \\
c_{j}(x) = 0, \;\;\; j = 1,2,\cdots, l
\end{matrix}\right. \; \Leftrightarrow \;
\left\{\begin{matrix}
\nabla f + \sum_{i=1}^{k}\lambda_{i} \nabla g_{i} + \sum_{j=1}^{l}\mu_{j} \nabla c_{j}= 0 \\
g_{i}(x) \leq 0, \; i = 1,2,\cdots,k \\
c_{j}(x) = 0, \; j = 1,2,\cdots,l \\
\lambda_{i} \geq 0, \; i = 1,2,\cdots,k \\
\lambda_{i} g_{i}(x) = 0, \; i = 1,2,\cdots,k
\end{matrix}\right.$$


