逻辑斯谛回归
先介绍一个分布：逻辑斯谛分布。
设 $X$ 是连续随机变量，且 $X$ 具有以下分布函数和概率密度：
$$F(x) = P(X \leq x) = \frac{1}{1 + e^{-\frac{x-\mu}{\gamma}}} \\
f(x) = F^{'}(x) = \frac{e^{-\frac{x-\mu}{\gamma}}}{\gamma(1 + e^{-\frac{x-\mu}{\gamma}})^{2}}$$
其中，$\mu$ 是随机变量的数学期望，$\lambda > 0$ 是形状参数。
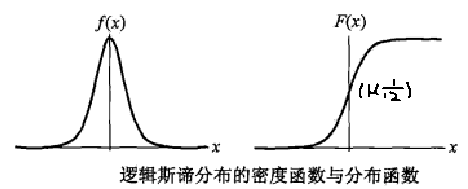
由图可以看出，逻辑斯谛分布和高斯分布的密度函数长得差不多。特别注意逻辑斯谛分布的概率密度函数自中心附近增长速度较快，而
在两端的增长速度相对较慢。形状参数 $\lambda$ 的值越小，$F(x)$ 在中心附近增长的越快。
逻辑斯谛回归的英文是：Logistic Regression，下面简称其为 LR 回归。
线性回归模型帮助我们用最简单的线性方程实现了对数据的拟合，但只实现了回归而无法进行分类。因此LR就是在线性回归的基础上，构造的一
种分类模型。对线性模型进行分类如二分类任务，简单的是通过阶跃函数($sgn$ 函数)，即将线性模型的输出值套上一个函数进行分割，但这样的
分段函数数学性质不好，既不连续也不可微。
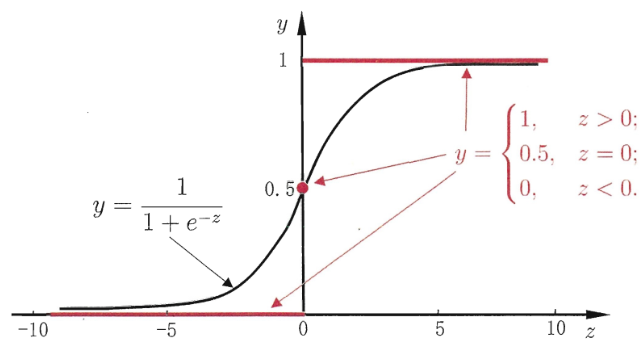
因此有人提出了对数几率函数，见上图，简称 $Sigmoid$ 函数。
$$y = \frac{1}{1 + e^{-x}} = \frac{e^{x}}{1 + e^{x}}$$
该函数具有很好的数学性质，既可以用于预测类别，并且任意阶可微，因此可用于求解最优解。这个函数能够将输出压缩在 $0-1$ 之间。
将分类超平面方程代入函数，可得：
$$y = \frac{1}{1 + e^{-(w^{T}x+b)}} = \frac{e^{w^{T}x+b}}{1 + e^{w^{T}x+b}}$$
函数的输出 $y$ 是有概率意味的，表达的是：当前测试样本属于类别 $1$ 的概率。由上可知：
$$1 - y = \frac{e^{-(w^{T}x+b)}}{1 + e^{-(w^{T}x+b)}} = \frac{1}{1 + e^{w^{T}x+b}}$$
若将 $y$ 视为样本 $x$ 作为正例的可能性，则 $1-y$ 是其反例的可能性，两者的比值称为几率（odds），反映了 $x$ 作为正例的相对可能性。
对几率取对数则得到对数几率：
$$\ln \frac{y}{1 - y} = w^{T}x+b$$
可以看出得到的超平面方程就是对数几率。将上面全部写成概率形式就是：
$$P(Y = 1 \;|\; X = x) = \frac{1}{1 + e^{-(w^{T}x+b)}} = \frac{e^{w^{T}x+b}}{1 + e^{w^{T}x+b}}$$
$$P(Y = 0 \;|\; X = x) = \frac{e^{-(w^{T}x+b)}}{1 + e^{-(w^{T}x+b)}} = \frac{1}{1 + e^{w^{T}x+b}}$$
$$\ln \frac{P(Y=1 \;|\; X = x)}{P(Y = 0 \;|\; X = x)} = w^{T}x+b$$
那如何预测输出呢？
对于给定的输入实例 $x$，比较 $P(Y = 1 \;|\; X = x), P(Y = 0 \;|\; X = x)$ 这两个条件概率的大小，将实例 $x$ 分到概率值较大的那一类。
从上面的过程可以看出，似乎是直接将 $Sigmoid$ 函数的输出当成了概率，下面用贝叶斯公式推导一下：
$$P(Y = 1 \;|\; X = x) = \frac{P(Y = 1 , X = x)}{P(X = x)} \\
= \frac{P(X = x \;|\; Y = 1)P(Y = 1)}{P(X = x \;|\; Y = 0)P(Y = 0) + P(X = x \;|\; Y = 1)P(Y = 1)} \\
= \frac{1}{1 + \frac{P(X = x \;|\; Y = 0)P(Y = 0)}{P(X = x \;|\; Y = 1)P(Y = 1)}}
= \frac{1}{1 + e^{-\ln \frac{P(X = x \;|\; Y = 1)P(Y = 1)}{P(X = x \;|\; Y = 0)P(Y = 0)}}} \\
= \frac{1}{1 + e^{-\ln \frac{P(Y = 1 \;|\; X = x)}{P(Y = 0 \;|\; X = x)}}} = \frac{1}{1 + e^{-\ln \frac{y}{1-y}}}$$
这个概率形式就和 $Sigmoid$ 的函数形式很像。所以说逻辑回归的模型表达式是有概率的原理在里面的，但前提是 $w^{T}x + b$ 这个回归表达式拟合的
是对数几率这种东西。也就是说最终训练出的 $w^{T}x + b$ 要使得这个线性回归表达式的输出为训练样本的对数几率。
那感受一下超平面方程能不能体现对数几率呢？
是可以的，不然这个模型也就不成立了。当点在超平面上时，分到正类还是负类的概率是相等的，所以相对几率就是 $0$，超平面方程输出也是 $0$，
所以两者是契合的。
模型参数估计
采用极大似然估计来求得参数 $w,b$。对于给定的训练数据集：
$$T = \left \{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\right \}$$
设：
$$P(Y = 1 \;|\; X = x) = \pi(x) \\
P(Y = 0 \;|\; X = x) = 1 - \pi(x)$$
则似然函数或这组样本出现的概率为：
$$L(w,b) = \prod_{i=1}^{n}[\pi(x_{i})]^{y_{i}}[1-\pi(x_{i})]^{1-y_{i}}$$
这个式子的意思是，对于每一个样本来说，找到参数使其属于真实标记的概率最大。
$$\ln L(w,b) = \sum_{i=1}^{n}\left [\; y_{i}\ln \pi(x_{i}) + (1-y_{i})\ln(1-\pi(x_{i}) ) \;\right ] \\
= \sum_{i=1}^{n}\left [\; y_{i}\ln \frac{\pi(x_{i})}{1-\pi(x_{i})} + \ln(1-\pi(x_{i}) ) \;\right ] \\
= \sum_{i=1}^{n}\left [\; y_{i}(w^{T}x_{i}+b) - \ln(1+e^{w^{T}x_{i} + b} ) \;\right ]$$
记
$$\hat{w} = \begin{bmatrix}
w\\
b
\end{bmatrix} ,\;
\hat{x}_{i} = \begin{bmatrix}
x_{i}\\
1
\end{bmatrix}$$
所以有：
$$\ln L(w,b) = \sum_{i=1}^{n}\left [\; y_{i}(\hat{w}^{T}\hat{x}_{i}) - \ln(1+e^{\hat{w}^{T}\hat{x}_{i}} ) \;\right ]$$
故损失函数为
$$J(\hat{w}) = \sum_{i=1}^{n}\left [\; -y_{i}(\hat{w}^{T}\hat{x}_{i}) + \ln(1+e^{\hat{w}^{T}\hat{x}_{i}} ) \;\right ]$$
逻辑斯谛回归学习中通常采用的方法是梯度下降法及拟牛顿法。下面介绍通过梯度下降法求解过程。
求偏导得：
$$\frac{\partial J}{\partial \hat{w}} = \sum_{i=1}^{n}\left [ \; -y_{i}\hat{x_{i}} + \frac{e^{\hat{w}^{T}\hat{x}_{i}}}{1+e^{\hat{w}^{T}\hat{x}_{i}}}\hat{x_{i}} \; \right ] = \sum_{i=1}^{n}\left [ \; -y_{i} + \pi(\hat{x_{i}}) \; \right ]\hat{x_{i}}$$
这里的 $y_{i}$ 是样本点的输出，只有 $0,1$ 两个值，不是概率，$\pi(\hat{x_{i}})$ 为样本输出为正类的概率。
在使用梯度下降法求解时，每次迭代地更新公式为：
$$\hat{w} = \hat{w} - \sum_{i=1}^{n}\left [ \; -y_{i} + \pi(\hat{x_{i}}) \; \right ]\hat{x_{i}}$$
