$k$ 近邻法
$k$ 近邻算法是一个有监督的机器学习算法,也被称为 $k-NN$ 算法,可以解决分类问题,也可以解决回归问题。
该方法的思路是:通过找出一个样本的 $k$ 个最近邻居,将这些邻居的某个(些)属性的平均值赋给该样本,就可以得到该样本对应属性的值。
$kNN$ 是懒惰学习(lazy learning)的典型代表,不具有显式的学习过程。懒惰学习技术在训练阶段仅仅将样本保存起来,训练开销为 $0$,等收
到测试样本时再进行处理,相应的,那些在训练阶段就对样本进行学习处理的方法,称为“急切学习”。
算法描述
训练数据集 $T = {(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})}$,其中输入 $x_{i}$ 为实例的特征向量,输出 $y_{i}$ 为实例对应的类别,
设 $y_{i} \in \left \{ c_{1},c_{2},...,c_{K} \right \}$。算法分为两步:
1)根据给定的距离度量,在训练集 $T$ 中找出与 $x$ 最邻近的 $k$ 个点,涵盖这 $k$ 个点的 $x$ 的邻域记作 $N_{k}(x)$。
2)在 $N_{k}(x)$ 中根据分类决策规则决定 $x$ 的类别 $y$:
$$y = arg \max_{c_{j}} \sum_{x_{i} \in N_{k}(x)}^{}I(y_{i} = c_{j}),\; i = 1,2,...,N;\;j = 1,2,...,K$$
$arg \; max$ 是指使得函数 $\sum_{x_{i} \in N_{k}(x)}$ 取得其最大值时所对应的自变量 $c_{j}$。
任意两个样本点之间的距离可以通过这两点所确定向量的范数来度量,可以用 $1,2,\infty$ 范数等,这里就不再赘述了。
$$L_{p}(x_{i},x_{j}) = \left ( \sum_{l=1}^{n}|x_{i}^{l} - x_{j}^{l}|^{p} \right )^{\frac{1}{p}}$$
$k$ 值的选择:
1)$k$ 值较小:训练误差会减小,测试误差会增大。例如像噪点,错误的数据,不恰当的度量标准以及数据本身的缺陷等,都会很大程度
上影响最终的结果,而如果 $k$ 值比较大,那么以上缺陷就会尽可能的平均,从而减小对最终结果的影响。
2)$k$ 值较大:训练误差会增大,测试误差会减小。因为与结果无关的元素被平均,影响减少,自然得出的模型会更可信。
分类决策规则:一般是多数表决,即 $k$ 个邻近的训练实例中的多数类决定输入实例的类。
算法实现
由上面的描述可以看出,这个算法本身是很简单的,那怎么实现呢?
$k$ 近邻法最简单的实现方法是线性扫描,这时要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时。所以主要考虑的
问题是如何对训练数据进行快速 $k$ 近邻搜索,这点在特征空间的维数大及训练数据容量大时尤其必要。
对于一维数据的查询可以使用常规的平衡二叉树,那对于多维数据的查询有没有类似的方法?
针对多维数据索引,引入 $kd$ 树。下面用一个二维的例子来直观得了解一下 $kd$ 树。
注意:$kd$ 树中的 $k$ 指的是向量维度,而不是 $k$ 近邻中的 $k$。
将每个学生的语文成绩和数学成绩构成一个二维的样本点,那么构建 $kd$ 树的基本思路就是:
1)先根据语文成绩,将所有人的成绩分成两半,其中一半的语文成绩 $\leq c_{1}$,另一半的语文成绩 $>c_{1}$,分别得到集合 $S_{1},S_{2}$。
2)针对 $S_{1}$,根据数学成绩分为两半,其中一半的数学成绩 $\leq m_{1}$,另一半的数学成绩 $> m_{1}$,分别得到集合 $S_{3},S_{4}$;
针对 $s_{2}$,根据数学成绩分为两半,其中一半的数学成绩 $\leq m_{2}$, 另一半的数学成绩 $> m_{2}$,分别得到集合 $S_{5},S_{6}$;
3)再根据语文成绩分别对 $S_{3},S_{4}$,$S_{5},S_{6}$ 继续执行类似划分得到更小的集合,然后再在更小的集合上根据数学成绩继续,...
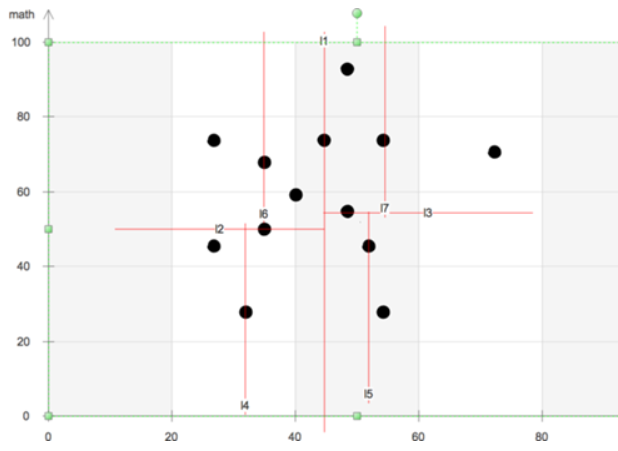
其中划一道竖线表示按语文成绩分,划一道横线表示按数学成绩分。
扩展到多维,相当于不断地用垂直于坐标轴的超平面将 $k$ 维空间切分,构成一系列的 $k$ 维超矩形区域。$kd$ 树的每个结点对应于一个 $k$ 维超矩形区域。
那对于每个维度的坐标系,怎么选取划分点呢?
构建平衡 $kd$ 树的方法:选择每个维度坐标的中位数作为划分点,由通过划分点并于坐标轴 $x^{l}$ 垂直的超平面进行分割。
这个落在超平面上的实例点就作为父节点。假如当前选择的是坐标轴 $l$,向量维度为 $k$,则生成该结点孩子结点所要选择的坐标轴就是
$$l = l \; mod \; k + 1$$
那如何用 $kd$ 树进行最近邻搜索呢?语言是苍白的,下面通过一个图来直观得理解搜索过程。
下面是一个已经划分好的空间,另有一个输入目标实例点 $S$,现在要找出距离 $S$ 最近的点。
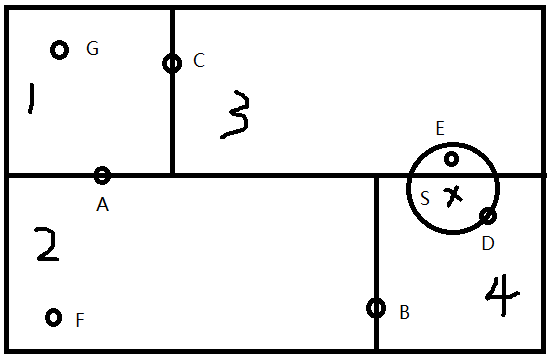
1)首先按维度来搜索 $kd$ 树,通过对比每个坐标分量确定 $S$ 位于哪个叶节点所在的区域,搜索后发现 $S$ 位于叶节点 $D$ 所在的区域 $4$。
不妨假设点 $D$ 就是 $S$ 的最近邻,那如果还存在真正的最近邻一定在以点 $S$ 为中心,通过点 $D$ 的圆的内部。这个圆在更高维空间里叫做"超球体"。
因为只有在超球体的内部,才能替代点 $D$ 成为最近邻。
2)回退到结点 $D$ 的父结点 $B$,这一步有两个检查。
a. 计算父结点 $B$ 到 $S$ 的距离,如果更近(即点 $B$ 在超球体内),则将点 $B$ 更新为当前最近邻。
b. 检查父结点的另一个子结点对应的超矩形区域是否与上面的那个超球体相交:
i. 如果不相交,继续回退,即找 $B$ 的父节点。
ii. 如果相交,意味着结点 $B$ 的另一个子树空间可能有到 $S$ 更近的点,递归地对父结点的另一子结点进行最近邻搜索。
注:每一个叶子结点独占一块超矩形区域,每个非叶子结点都位于用来切割的超平面上。
那如何判断相交呢?比如判断上图中区域 $2$ 是否与超球体有交集,很明显,区域 $2$ 和 $4$ 是通过 $B$ 所在的垂直坐标轴的超平面划分的,如果超球体
到这个分割超平面的距离小于半径,则不相交,大于半径,则相交。
3)递归地向上回退,对每个父节点都执行 2)中的两步操作。
该算法针对最近邻,$k$ 近邻在搜索最近邻的基础上,忽略之前找到的最近邻实例,重新选择最近邻,重复 $k$ 次,得到目标点的 $k$ 个最近邻。
至于实现方法则有多种,这里不讨论。
$KNN$ 优缺点
优点:
1)结构简单;
2)无数据输入假定,准确度高,对异常点不敏感。
缺点:
1)计算复杂度高、空间复杂度高;
2)样本不平衡时,对稀有类别预测准确度低;
3)使用懒惰学习,预测速度慢。


