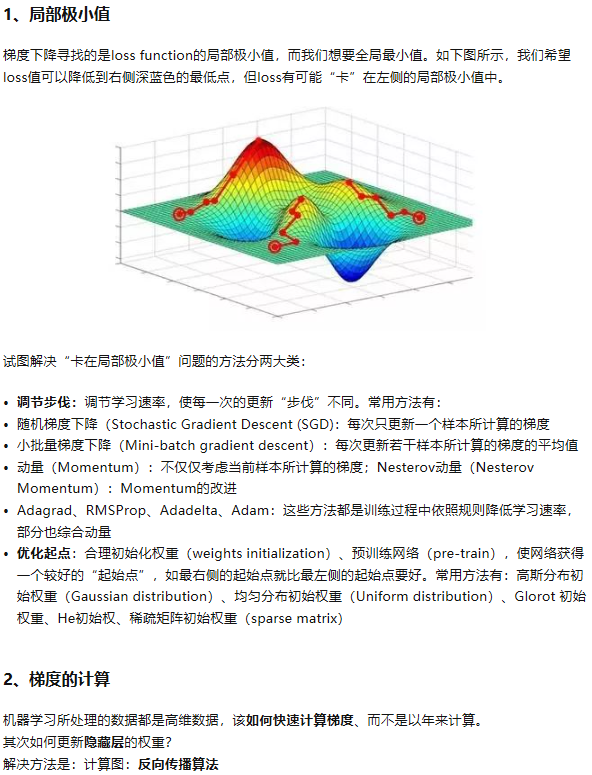
梯度下降法
看本篇博客之前,首先得先去了解一下什么是梯度。梯度下降算法的思想,它将按如下操作达到最低点:
1)明确自己现在所处的位置。
2)找到相对于该位置而言下降最快的方向。
3)沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低。
4)回到第一步。
5)终止于最低点。
从数学角度来看,多元函数的梯度方向是函数增长最快的方向,那么梯度的反方向就是函数减少最快的方向。
以二元函数为例:
$$z = f(x,y)$$
现在确定一个点 $(x_{0},y_{0})$,这个点是水平面上的,即在 $xoy$ 平面上,考虑在这个点上,往平面的哪个方向走相同的
一小段距离,对应的函数值 $z$ 会是最小。
或者:以 $(x_{0},y_{0})$ 为圆心,画一个小半圆,圆上哪个点对应的 $z$ 值会最小?
了解了梯度,可知在梯度反方向走一小段距离对应的函数值将会最小。这就相当于贪心算法,我每次都走的是局部最小,那走到
最后必然也是局部最小的。当然这样做无法保证全局最优,在不同的位置进行梯度下降,找到的“最小值”都可能会不同。
$$l = -(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$
我们代入具体的值,即将 $x = x_{0},y = y_{0}$ 代入就会得到一个具体的向量,这个向量以原点为起始点,它的模代表该点在
该方向上的变化率。将这个具体的向量表示成如下形式:
$$l_{0} = -(\frac{\partial f}{\partial x_{0}},\frac{\partial f}{\partial y_{0}})$$
设 $\alpha$ 是移动的距离和向量 $l_{0}$ 模长的一个比例,用它来控制点 $(x_{0},y_{0})$ 在 $l_{0}$ 上移动的距离,即移动的距离为
$$d = \alpha \cdot |l_{0}|, \alpha > 0$$
那么此时 $(x_{0},y_{0})$ 的坐标会变成这样:
$$x_{0} = x_{0} - \alpha \cdot \frac{\partial f}{\partial x_{0}} \\
y_{0} = y_{0} - \alpha \cdot \frac{\partial f}{\partial y_{0}}$$
这很容易理解,我们移动射线上的 $d$ 距离,将它进行分解,相当于各个分量也移动相同比例的距离。
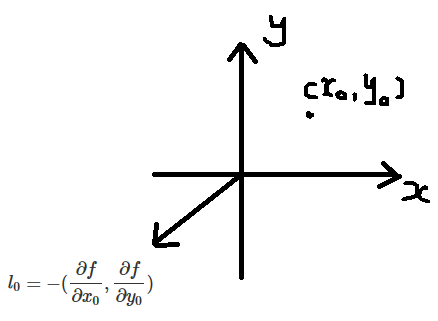
那迭代到什么时候停止呢?
可以设置一个精度,当迭代到某一个点时,如果求出的梯度向量的模小于这个精度,就停止迭代,这个模代表的是函数值在该方向的变化率。
当变化率很小的时候,即坡度很平了,就认为达到局部最小。
由泰勒公式推导梯度下降法
梯度下降法的背后,其实还是离不开多元函数的一阶泰勒展开以及函数的线性近似的思想。一个函数的泰勒展开式为:
$$f(x) = f(x_{0}) + \nabla f(x_{0})^{T}\Delta x + \frac{1}{2}\Delta x^{T}G(x_{0})\Delta x + \cdots$$
现在我们只考虑展开到一阶的情形:
$$f(x) = f(x_{0}) + \nabla f(x_{0})^{T}(x - x_{0})$$
因为泰勒公式反映的是函数在展开点处的局部性质,所以这个一阶的泰勒近似是在 $x_{0}$ 的小邻域内近似效果较好,因此迭代的步伐不能
迈得过大,太大的话,$x_{0}$ 处近似的精度就失效了。
现在我们用这个一阶的泰勒展开式来代替函数在 $x_{0}$ 局部区域内的函数,那下一个点该怎么选才能使函数值下降最大呢?
当确定 $x_{0}$ 后,$f(x_{0})$ 就是已知的,那么函数值取决于第二项的两个向量点积:
$$\nabla f(x_{0})^{T}(x - x_{0}) = |\nabla f(x_{0})||x - x_{0}|\cos \theta = \lambda \cdot |\nabla f(x_{0})| \cdot \cos \theta$$
其中 $\lambda > 0$ 是向量 $x - x_{0}$ 的模,$\theta$ 是两向量之间的夹角。
那么对于相同模长 $\lambda$,该怎么选择方向(就是选择 $\theta$),才会使函数值最小呢?
很明显就是当向量 $x - x_{0}$ 和 $\nabla f(x_{0})$ 方向相反时,相同模长 $\lambda$ 对应的函数值最小,即:
$$x - x_{0} = - \lambda \cdot \frac{\nabla f(x_{0})}{|\nabla f(x_{0})|}$$
所以:
$$x = x_{0} - \lambda \cdot \frac{\nabla f(x_{0})}{|\nabla f(x_{0})|}$$
注意:上面这个推导过程是建立在邻域内的,这样泰勒的一阶展开近似才成立,如果 $\lambda$ 取太大,近似就不成立了。
梯度下降法的缺点