超平面
定义:$n$ 维线性空间中维度为 $n - 1$ 的子空间,它可以把线性空间分割为不相交的两部分。
这里的 $n$ 必须大于 $3$,其子空间才能称之为超平面。
更直观得来理解超平面:超平面其实就是平面中的直线、空间中的平面之推广。在三维坐标系里,$XoY$ 平面把三维坐标系”分割”成
两个空间,这个分割平面引申到一维,二维,四维空间…来,他就是一个超平面。一维里是一个点分割空间,二维里是条线,三维刚好是
个平面,四维的用几何已经无法表示了,但是我们赋予这个分割的东西为超平面,就比较形象了。
超平面方程推导:
1)平面直线方程
对于平面上的任意一条直线,它的一般方程为:
$$ax + by + c = 0$$
从向量角度来看,一般方程可以写成如下形式
$$\begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix} + c = 0$$
可以发现:直线其实就是一个常向量和另一个变化的向量的内积为定值 $c$。
其中 $x,y$ 代表直线上任意一点的坐标,所以 $(x,y)^{T}$ 表示从原点出发到直线上任意一点的射线构成的向量。
那向量 $(a,b)^{T}$ 是啥呢?看个图:
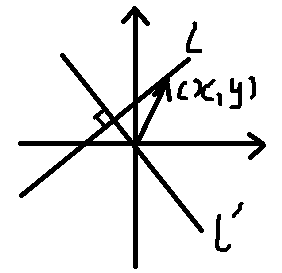
我们知道向量内积表示:一个向量乘以另一个向量在该向量上的正交投影。如果不懂可先去阅读博客。
那能否找到一个向量,这个向量必须满足:向量 $(x,y)^{T}$ 在它上面的投影都一样。这样才能保证内积为定值。
这样的向量只有一个,那便是直线 $l$ 的法向量 $l^{'}$。所以常向量 $(a,b)^{T}$ 就是直线的法向量。
不同的法向量 $(a,b)^{T}$ 或者不同的定值 $c$ 就意味着不同的直线方程。
注意:上面的直线方程都是化成最简的形式,即两边系数不可再约,不然两边同时乘上一个数,虽然法向量和定值变了,
但表示的直线却没变,所以只在最简形式法向量和定值才与直线一一对应。
2)空间平面方程
对于空间上的任意一个平面,它的一般方程为:
$$ax + by + cz + d = 0$$
从向量角度来看,一般方程可以写成如下形式
$$\begin{bmatrix}
a & b & c
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix} + d = 0$$
和平面直线类似,上面这个方程可以理解为:一个常向量和另一个变化的向量的内积为定值 $d$。
其中常向量为这个平面的法向量,变化的向量为原点到平面上任意一点的射线构成的向量。
3)引申到超平面
一个超平面的法向量:意味着它要垂直于该超平面内的任一个向量。
对于 $4$ 维空间来说,它的超平面就是一个 $3$ 维空间,很难想象会存在一个向量,它垂直于三维空间中的任一个向量。
我们没办法想象到三维以上的空间长啥样,但数学是纯粹逻辑上的东西,高维空间在逻辑上是存在的。
设 $n$ 维空间中的一个超平面的法向量为 $w = (w_{1},w_{2},...,w_{n})^{T}$,原点到该超平面上任意一点的向量为 $x^{T} = (x_{1},x_{2},..,x_{n})$。
由直线方程、平面方程进行推广,可知超平面方程为
$$w^{T}x + b = 0$$
点到超平面的距离推导:
1)点到平面直线的距离公式
任一点 $(x_{0},y_{0})$ 到直线 $ax+by+c = 0$ 的距离公式为
$$d = \frac{|ax_{0} + by_{0} + c|}{\sqrt{a^{2} + b^{2}}}$$
如下示意图:
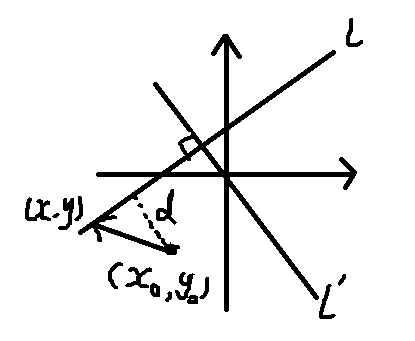
在直线上任取一点 $(x,y)$,考虑向量
$$(x-x_{0},y-y_{0})^{T}$$
图中的 $d$ 就是我们所要求的点到直线的距离,向量点积代表:一个向量乘以另一个向量在该向量上的正交投影。
而 $d$ 显然就是向量 $(x-x_{0},y-y_{0})^{T}$ 在法线向量上的投影的绝对值。所以
$$\begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x-x_{0} \\
y-y_{0}
\end{bmatrix} = \pm \sqrt{a^{2}+b^{2}} \cdot d$$
继续转化
$$\begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix} -
\begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x_{0} \\
y_{0}
\end{bmatrix} =
-c -
\begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x_{0} \\
y_{0}
\end{bmatrix} =
\pm \sqrt{a^{2}+b^{2}} \cdot d$$
所以距离 $d$ 为
$$d = \frac{| \begin{bmatrix}
a & b
\end{bmatrix}
\begin{bmatrix}
x_{0} \\
y_{0}
\end{bmatrix} + c\;|}{\sqrt{a^{2}+b^{2}}}$$
2)点到空间平面的距离公式
我们按照上面的思路也可以列出方程:
$$\begin{bmatrix}
a & b & c
\end{bmatrix}
\begin{bmatrix}
x-x_{0} \\
y-y_{0} \\
z-z_{0}
\end{bmatrix} = \pm \sqrt{a^{2}+b^{2}+c^{2}} \cdot d$$
所以距离 $d$ 为
$$d = \frac{| \begin{bmatrix}
a & b & c
\end{bmatrix}
\begin{bmatrix}
x_{0} \\
y_{0} \\
z_{0}
\end{bmatrix} + d\;|}{\sqrt{a^{2}+b^{2}+c^{2}}}$$
3)引申到超平面
已知超平面方程为 $w^{T}x + b = 0$。
类比于点到直线和平面的距离公式,有
$$d = \frac{| w \cdot x_{i} + d\;|}{||w||_{2}}$$
向量 $w$ 的 $L_{2}$ 范数就是向量的模,$\hat{x}$ 表示具体的某一个点,$d$ 就是该点到超平面的距离。
注:$x_{i}$ 表示某个具体向量,而不是表示坐标分量,它的坐标分量用另一种记法,即
$$x_{i} = (x^{(1)},x^{(2)},...,x^{(n)})^{T}$$
判断超平面的正反
一个超平面可以将它所在的空间分为两半, 它的法向量指向的那一半对应的一面是它的正面, 另一面则是它的反面。
那如何判断一个点位于超平面内,还是超平面的正面,或者反面呢?
点 $x$ 在超平面上有
$$w^{T}x + b = 0$$
若点 $x$ 在超平面的正面,考虑到 $wx$ 其实就是向量 $w$ 的模(为正)乘上 $x$ 在它上面的投影(可正可负),考虑函数
$$y = ax,a > 0$$
上式是一个递增函数,所以当 $x$ 往正方向移动时,$y$ 是变大的,所以若点 $x$ 在超平面的正面,有
$$w^{T}x + b > 0$$
若点 $x$ 在超平面的反面,有
$$w^{T}x + b < 0$$
若将距离公式中分子的绝对值去掉, 让它可以为正为负. 那么, 它的值正得越大, 代表点在平面的正向且与平面的距离越远。
反之, 它的值负得越大, 代表点在平面的反向且与平面的距离越远。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号