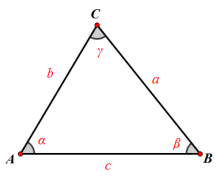
余弦定理

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍，即

$$c^{2} = a^{2}+b^{2}-2ab\cos \gamma \\
b^{2} = c^{2}+a^{2}-2ac\cos \beta  \\
a^{2} = b^{2}+c^{2}-2bc\cos \alpha $$

                  

从直观上来看，余弦定理很像勾股定理，只不过，多了最后一项，当角度为 $90$ 度时，公式就完全变成勾股定理了，所以余弦定理

可以理解为是勾股定理在一般三角形中的扩展。

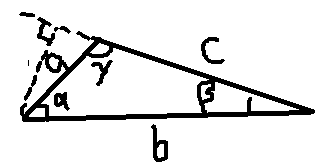
它的证明非常简单，可依托勾股定理，如下图

                          

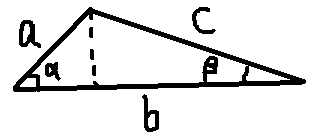
$$c^{2} = (a\sin \alpha )^{2} + (b - a \cos \alpha)^{2} = a^{2}\sin^{2}\alpha + a^{2}\cos^{2}\alpha +
b^{2} - 2ab\cos\alpha = a^{2} + b^{2} - 2ab\cos \alpha$$

$$a^{2} = (c\sin \beta )^{2} + (b - c \cos \beta)^{2} = c^{2}\sin^{2}\beta + c^{2}\cos^{2}\beta +
b^{2} - 2bc\cos\beta = b^{2} + c^{2} - 2bc\cos \beta $$

$$b^{2} = \left [\; a\sin \left ( \pi -\gamma \right ) \;\right]^{2} + \left [ \; c + a \cos \left ( \pi -\gamma \right ) \; \right ]^{2} = a^{2}\sin^{2}\gamma  + a^{2}\cos^{2}\gamma  +
c^{2} - 2ac\cos\gamma  = a^{2} + c^{2} - 2ac\cos \gamma$$