矩阵相似

相似是研究线性变换矩阵之间的关系，首先需要确定一个线性空间，这是必要的，研究不同线性空间中变换矩阵的关系没啥意义，确

定了线性空间，那么向量的维数，基中向量的个数都被定下来了。

定义：若 $A$ 和 $B$ 都是 $n$ 阶矩阵，如果存在可逆矩阵 $P$，使得 $P^{-1}AP = B$，则称矩阵 $A$ 与 $B$ 相似，记为 $A\sim B$。

理解相似矩阵，得先理解线性变换。

通俗一点来描述相似矩阵：同一个线性变换，不同参考系下的矩阵，称为相似矩阵。

为什么我们需要相似矩阵呢？

对空间中的某一个向量做变换，需要先确定线性空间，并选定一组基来建立坐标系，选择的坐标系越复杂，所做的变换也就越复杂，

计算量也越大，比如，需要将空间中的某一个向量 $\alpha$ 逆时针旋转 $45$ 度，下面是选择的几组参考系：

         

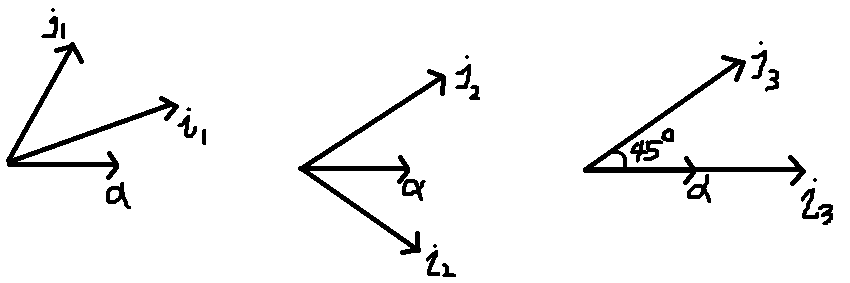
很明显在第三种坐标系，很容易写出向量 $\alpha$ 逆时针旋转 $45$ 度后的坐标。

所以：相似矩阵的目的是为了找到更简单的坐标系来描述变换。

注：如果能选取不同基，使线性变换的矩阵变成对角矩阵，那么，线性变换的形式就会变得相对简单。

建立不同的参考系，逆时针旋转 $45$ 度这个变换的矩阵都不一样，但是它们描述的是同一个线性变换，即本家兄弟，见面不认识，岂不成了笑

话。好在，我们可以找到同一个线性变换的矩阵兄弟们的一个性质，那就是：一定能找到一个非奇异矩阵 $P$，使得

$$P^{-1}AP = B$$

这个 $P$ 就是基 $(i_{1},j_{1})$ 到基 $(i_{2},j_{2})$ 的过渡矩阵，即

$$(i_{2},j_{2}) = (i_{1},j_{1}) \cdot P$$

设向量 $\alpha$ 在基 $i_{1},j_{1}$ 下的坐标为 $v_{1} = (x_{1},y_{1})^{T}$，在基 $i_{2},j_{2}$ 下的坐标为 $v_{2} = (x_{2},y_{2})^{T}$，于是

$$P \cdot v_{2} = v_{1}$$

设逆时针旋转 $45$ 度在基 $i_{1},j_{1}$ 下的变换矩阵为 $A$，在基 $i_{2},j_{2}$ 下的变换矩阵为 $B$，基于两个参考系的坐标变换关系有

$$Av_{1} = PBv_{2}$$

由 $v_{1}$ 和 $v_{2}$ 的关系有

$$APv_{2} = PBv_{2}$$

故

$$P^{-1}AP = B$$

 

当变换矩阵满足什么样的条件时，可以相似对角化？

设基向量 $(i,j)^{T}$，变换矩阵 $A$，向量 $\alpha = (a,b)$，则

$$A \begin{bmatrix}
i\\
j
\end{bmatrix}(a,b)$$

所以，线性变换其实是先作用于基向量，然后在进行矢量合成，现在我们要找一组基，使得线性变换 $A$ 在这组基的每一个向量上都是伸缩变换。

不妨将要找的这组基记为 $Q$，$Q$ 的参考系仍为 $S$，显然矩阵 $A$ 的特征向量符合条件，同一个线性变换 $A$ 对它自己的特征向量的作用效果

就仅是进行伸缩而不是旋转。

总结一下：相同的线性变换，作用于基向量 $S$ 会发生旋转和伸缩，而作用于基向量 $Q$ 仅会发生伸缩。

现在将 $Q$ 作为参考系($Q$ 不放到 $S$ 中了)，找一个矩阵 $B$ 和 $A$ 相似，就是意味着：$B$ 对参考系 $Q$ 的作用效果 $=$ 在参考系 $S$ 中，$A$ 对 $Q$ 的作用效果。

那 $A$ 对 $Q$ 产生了什么效果？伸缩了倍数为对应的特征值，那么要想 $B$ 也有这样的效果，那 $B$ 必然是特征值构成的对角矩阵了。

定理：线性变换矩阵有 $n$ 个线性无关的特征向量 $\Leftrightarrow$ 可相似对角化。

这个怎么理解呢？

设一个变换矩阵 $A$，它所在的参考系为 $S$，$A$ 有 $n$ 个线性无关的特征向量 $\alpha_{1},\alpha_{2},...,\alpha_{n}$，设矩阵 $P$ 为

$$P = [\alpha_{1},\alpha_{2},...,\alpha_{n}] $$

现在我们以这 $n$ 个线性无关的特征向量作为新的基，将 $P$ 作为过渡矩阵，此时变换矩阵 $A$ 相对于新的基变成什么了呢？

设这 $n$ 个特征向量对应的特征值分别为 $\lambda_{1},\lambda_{2},...,\lambda_{n}$，则易知

$$A[\;\alpha_{1},\alpha_{2},...,\alpha_{n}\;] = [\;\lambda_{1}\alpha_{1},\lambda_{2}\alpha_{2},...,\lambda_{n}\alpha_{n}\;] =
[\;\alpha_{1},\alpha_{2},...,\alpha_{n}\;]
\begin{bmatrix}
\lambda_{1} &  &  & \\
 & \lambda_{2} &  & \\
 &  & ... & \\
 &  &  & \lambda_{b}
\end{bmatrix}$$

即在过渡矩阵 $P$ 下，变换 $A$ 变成了

$$P^{-1}AP = \begin{bmatrix}
\lambda_{1} &  &  & \\
 & \lambda_{2} &  & \\
 &  & ... & \\
 &  &  & \lambda_{b}
\end{bmatrix}$$

注：作为基的每个向量的单位长度不一定要相等，比如 $x$ 轴和 $y$ 轴的单位长度也可以不必相等。