矩阵的运算和分块
矩阵:数域 $F$ 上 $m*n$ 个数构成的数表。
虽然它只是一个数表,但这组数可以赋予多个不同的含义,如向量,方程系数,线性变换等,理解的角度不同,矩阵的运算便代表不同的含义。
单纯来看矩阵,其实就是一种书写手法,正是赋予了相应地运算,才能够使其具有一定地表现力。
1. 下面介绍下矩阵定义了哪些基本运算。
1)加减运算:两个 $m \times n$ 的矩阵 $A = (a_{ij}),B = (b_{ij})$,两个必须为同型矩阵,它们的加法规定为
$$(A+B)_{ij} = a_{ij} + b_{ij}$$
2)数乘运算:数 $k$ 与矩阵 $A$ 的乘积,记为 $Ak$ 或者 $kA$,规则为
$$(kA)_{ij} = (Ak)_{ij} = ka_{ij}$$
3)矩阵转置:把矩阵 $A$ 的行换成同序数的列得到的新矩阵,称为 $A$ 的转置矩阵,其规则为
$$A^{T} = (a_{ji})$$
4)矩阵相乘:设矩阵 $A=(a_{ij})_{ms}\;,B=(b_{ij})_{sn}$,两个矩阵不必为同型矩阵,其乘法运算规定为
$$AB = \left ( \sum_{k=1}^{s}a_{ik}b_{kj} \right )_{m\times n}$$
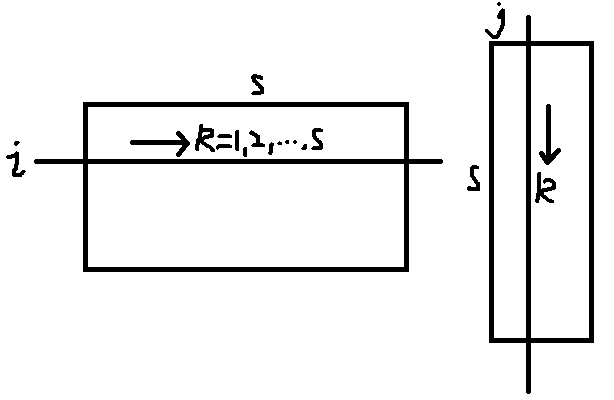
以 $k$ 来遍历,对于 $A$ 矩阵,$k$ 遍历第 $i$ 行的每一个元素,对于 $B$ 矩阵,$k$ 遍历第 $j$ 列的每一个元素,由于使用一个计数变量 $k$,
故相乘的两个矩阵必须满足前一个矩阵的列数等于后一个矩阵的行数。第 $i$ 行第 $j$ 列的内积和作为结果矩阵第 $i$ 行第 $j$ 列的值。
这样规定矩阵的乘法后,发现它具有很多合理性:
1)满足结合律:$ABC$ = $A(BC)$
2)满足分配律:$A(B+C)$ = $AB+AC$
但是不满足交换律,即 $AB \neq BA$。
是不是很神奇,下面我们对结合律做一个证明:
设矩阵 $A=(a_{ij})_{mn}\;,B=(b_{ij})_{np}\;,C=(c_{ij})_{pq}$,则
$$(ABC)_{ij} = \sum_{k=1}^{p}(AB)_{ik}C_{kj} \\
= \sum_{k=1}^{p}\left ( \sum_{l=1}^{n}A_{il}B_{lk} \right )C_{kj} \\
= \sum_{k=1}^{p}\left ( \sum_{l=1}^{n}A_{il}B_{lk}C_{kj} \right ) \\
= \sum_{l=1}^{n}\left (\sum_{k=1}^{p} A_{il}B_{lk}C_{kj} \right ) \\
= \sum_{l=1}^{n}A_{il}\left (\sum_{k=1}^{p}B_{lk}C_{kj} \right ) \\
= \sum_{l=1}^{n}A_{il}\left (BC \right )_{lj} = (A(BC))_{ij}$$
注:理解连续求和,需要从外向内解读,相当于嵌套的 $for$ 循环。
2. 分块矩阵
分块矩阵是一种计算手段。将一个矩阵用若干条横线和竖线分成许多个小矩阵,将每个小矩阵称为这个矩阵的子块,以子块为元素的形式上的矩阵称为分块矩阵。
分块矩阵是一种计算手段。对矩阵进行适当分块,可使高阶矩阵的运算可以转化为低阶矩阵的运算,同时也使原矩阵的结构显得简单而清晰,从而能够大大简化运算步骤。
有了分块矩阵,意味着矩阵中的元素不一定就是数值,也可以是一个矩阵,若干个子矩阵构成一个大矩阵,宛如程序中的递归。
为什么可以对矩阵分块呢?
1)加法的结合性,即分块子向量内积的和等于不分块向量的内积。
2)矩阵可以看作是一系列元素拼接起来的,而划分是其反操作。
下面介绍两种典型的分块方式,对于 $AB=C$,可以有
1)按行分块:对 $B,C$ 按行分块
$$\begin{bmatrix}
a_{11} & a_{12} & ... & a_{1n} \\
a_{21} & a_{22} & ... & a_{2n} \\
... & ... & ... & ... \\
a_{n1} & a_{n2} & ... & a_{nn}
\end{bmatrix} \cdot
\begin{bmatrix}
\beta_{1}\\
\beta_{2}\\
...\\
\beta_{n}
\end{bmatrix} =
\begin{bmatrix}
\alpha_{1}\\
\alpha_{2}\\
...\\
\alpha_{n}
\end{bmatrix}$$
可见矩阵 $C$ 的行向量可由 $B$ 的行向量线性表出。
2)按列分块:对 $A,C$ 按列分块
$$\begin{bmatrix}
\alpha_{1} & \alpha_{2} & ... & \alpha_{n}
\end{bmatrix} \cdot
\begin{bmatrix}
b_{11} & b_{12} & ... & b_{1n} \\
b_{21} & b_{22} & ... & b_{2n} \\
... & ... & ... & ... \\
b_{n1} & b_{n2} & ... & b_{nn}
\end{bmatrix} =
\begin{bmatrix}
\beta_{1} & \beta_{2} & ... & \beta_{n}
\end{bmatrix}$$
可见矩阵 $C$ 的列向量可由 $A$ 的列向量线性表出
上述分块方法提供了一种矩阵相乘的计算方式,以按行分块为例。
我们可以不必一个一个元素地计算,而可以直接得到新矩阵的一整行元素,如
$$\alpha_{1} = a_{11}\beta_{1} + a_{12}\beta_{2} + ... + a_{1n}\beta_{n}$$
即用 $a_{11}$ 乘上矩阵 $B$ 的第 $1$ 行元素,$a_{12}$ 乘上矩阵 $B$ 的第 $2$ 行元素,$a_{1n}$ 乘上矩阵 $B$ 的第 $n$ 行元素,然后累加,就可以得到新矩阵的第一行元素。
对于矩阵相乘 $AB=C$,我们可以这样理解:
1)矩阵 $C$ 的每一个行向量是矩阵 $B$ 的行向量的线性组合,组合的系数是矩阵 $A$ 的每一行。
2)矩阵 $C$ 的每一个列向量是矩阵 $A$ 的列向量的线性组合,组合的系数是矩阵 $B$ 的每一列。


