函数的凹凸性

设函数 $f(x)$ 在区间 $I$ 上有定义，在 $I$ 内任取两点 $x_{1},x_{2}$，对任意的 $\lambda \in (0,1)$，有 $\lambda x_{1} + (1-\lambda )x_{2} \in (x_{1},x_{2})$。

   

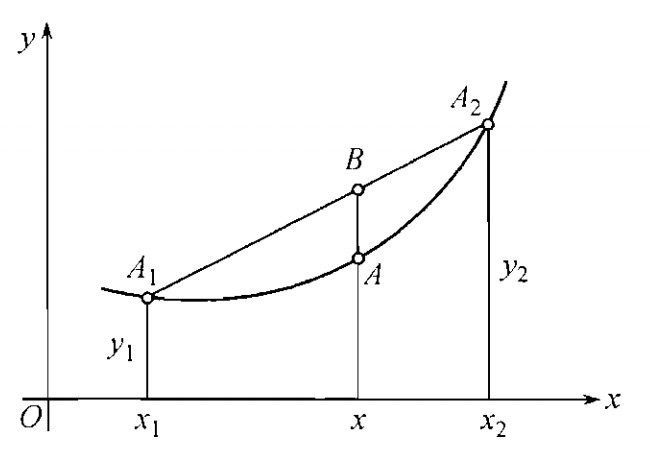
$A_{1}$ 点坐标 $(x_{1},f(x_{1}))$，$A_{2}$ 点坐标 $(x_{2},f(x_{1}))$，$A$ 点坐标 $(x,f(x))$，于是可以求得

$$y_{B} = \frac{x_{2}-x}{x_{2}-x_{1}}f(x_{1}) + \frac{x-x_{1}}{x_{2}-x_{1}}f(x_{2})$$

令 $\lambda = \frac{x_{2}-x}{x_{2}-x_{1}}$，则

$$y_{B} = \lambda f(x_{1}) + (1-\lambda )f(x_{2})$$

易推出

$$x = \lambda x_{1} + (1-\lambda )x_{2}$$

结合图像有

$$y_{A} < y_{B}$$

所以

$$f(x) \leq \frac{x_{2}-x}{x_{2}-x_{1}}f(x_{1}) + \frac{x-x_{1}}{x_{2}-x_{1}}f(x_{2})$$

即

$$f[\lambda x_{1} + (1-\lambda )x_{2}] \leq \lambda f(x_{1}) + (1-\lambda )f(x_{2}),\lambda \in (0,1)$$

当 $x_{1} \rightarrow x_{2}$，上式等号成立。

满足这个性质的函数称为凹函数，凸函数的定义与此类似，不在赘述。