函数间断点

函数连续性：从直观上看，函数连续性指的是函数值 $f(x)$ 随自变量 $x$ 变化的特性，当自变量 $x$ 的变化越小时，所引起的因变量

$f(x)$ 的变化也越小，即函数值无跃变。要说明函数在某一个点连续，只需说明自变量在趋近该点时函数值的变化是连续的，使用极

限来描述这个动态的过程。函数 $f(x)$ 在某一个点 $x_{0}$ 处连续必须同时满足 3 个条件：

    1）函数在 $x_{0}$ 处有定义

    2）$\lim_{x\rightarrow x_{0}}f(x)$ 存在

    3）$\lim_{x\rightarrow x_{0}}f(x) = f(x_{0})$

函数的连续性是由极限得到的，按照极限的定义知：这个函数首先必须在 $x_{0}$ 的邻域内有定义。

邻域内每个点都有定义并不代表函数在该邻域连续，如狄利克雷函数就处处不连续，却处处有定义。

也就是说：函数在一个点连续，只是说明函数在该点邻域内的变化是连续的，无法说明函数在该点邻域内连续。

举个例子：函数 $f(x) = x^{2}D(x)$ 只在 $x = 0$ 处连续，说明在 $x = 0$ 的邻域内，函数值随自变量的变化是连续的，这是由于

函数 $D(x)$ 的稠密性造成的，邻域内虽然处处不连续，但却处处有定义。

 

函数间断：函数 $f(x)$ 在某一个点 $x_{0}$ 的去心邻域有定义，但在点 $x_{0}$ 不连续，即上面三个条件不全满足，则函数在该点间断，

          该点为间断点。间断点可以有定义也可无定义，间断只是考虑极限，而极限只与该点左右极限有关，和点的取值无关。

   1）第一类间断点

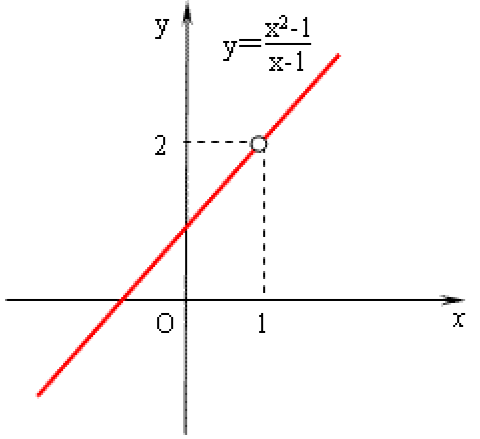
      a. 可去间断点：函数 $f(x)$ 在 $x_{0}$ 处左右极限都存在且相等，即该点处极限存在。若 $f(x)$ 在 $x_{0}$ 处有定义，则$\lim_{x\rightarrow x_{0}}f(x) \neq  f(x_{0})$。

                 

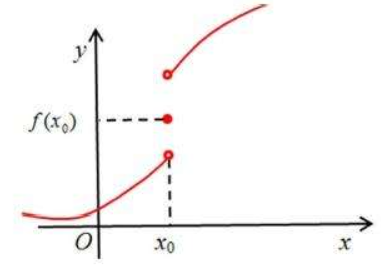
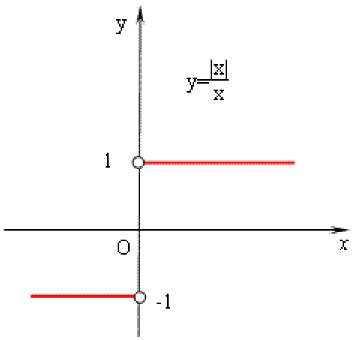
      b. 跳跃间断点：$f(x)$ 在 $x_{0}$ 处左右极限都存在但不相等。

                 

   2）第二类间断点

      a. 无穷间断点：左右极限至少有一个不存在(不存在就是为 $\infty$ )。

            

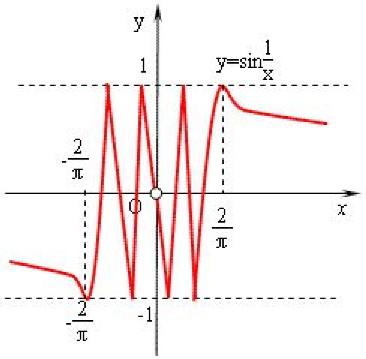
      b. 振荡间断点：间断点处的极限振荡不存在，此处是振荡不存在，并不是极限为无穷。下图函数，当 $x\rightarrow 0$，函数值在 -1和1之间交替取值。