数域

数域 $P$ 是一个数的集合，其中包含 $0$ 和 $1$，$P$ 中任意两个数的和、差、积、商（除数不为0）仍是 $P$ 中的数(封闭性)。

任何一个数域都得包含 $0$ 和 $1$，不然数运算的结果为 $0$ 或 $1$ 的话，将不再属于该数域。

证明一个数的集合是数域，即证明它对加减乘除封闭。

 

1. 实数域 $R$

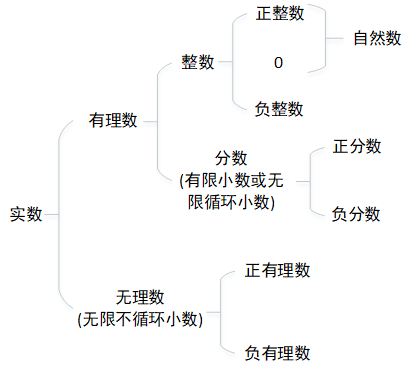
   实数，是一种能和数轴上的点一一对应的数。本来实数只叫作“数”，后来引入的虚数概念，数系扩充到复数系，原本的数便称作“实数”，意义是“实在的数”。

   实数是一维的数，即只能生活在一维的数轴上。

    

 

2. 复数域 $C$

   实数是一维的数，而复数生活在二维复平面，拥有更大的自由度。复平面是用水平的实轴与垂直的虚轴建立起来的复数的几何表示。

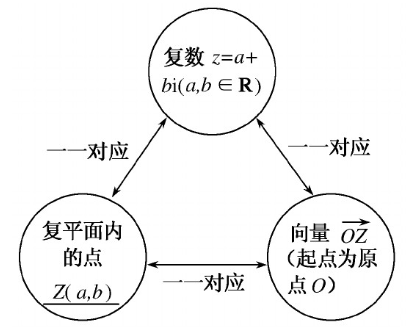
   复数的理解：

      1）复数首先是一个数值，数学表示为 $z = a + bi$。

      2）复数也是复平面上的任意一个点，它的坐标为 $(a,b)$。

      3）复平面上的每一个点和原点连线后构成一个既有大小又有方向的向量，因此复数也就可以看做是复平面上的一个向量。

     

   模：复数的模即向量的模 $z = \sqrt{a^{2} + b^{2}}$。

   幅角：复平面上的向量与实轴正方向的夹角。辐角可以有无穷多个值，它们相差 $2\pi$ 整数倍，但主辐角 $Argz$ 只有一个值 $\theta_{0} \in [-\pi,\pi]$，有

$$
Arg\left ( z \right ) = \left\{\begin{matrix}
\arctan \left ( \frac{b}{a} \right ),  & a>0 \\
\pm \frac{\pi}{2}, & a = 0,b \neq 0 \\
\arctan \left ( \frac{b}{a} \right ) + \pi , & a < 0,b\geq 0\\
\arctan \left ( \frac{b}{a} \right ) - \pi,& a < 0, b < 0
\end{matrix}\right.
$$

   可以感受到，复数是一个向量，有长度，有方向，有角度，那么复数的运算完全可以看成是一种向量变换，即一种包含长度，角度等特征的数的变换。

      1）任意一个复数乘以 $i$ 等价于：将向量逆时针旋转 90°。

      2）任意一个复数乘以 $-i$ 等价于：将向量顺时针旋转 90°。

      3）两个复数相乘就是：让它们的模长相乘得到最终的模长，让它们的幅角相加得到最终的幅角。

   举个例子：比如 $x^{2} = -1$，这个方程在实数域是没有解的，但如果将整个方程放到复数域，即方程中所有的数现在都是复平面上的点，则得到的解是 $i$，

             即 $1 * i * i = -1$，按复数变换来理解，就是复平面上的复数 $1$ 逆时针旋转 180°变为复数 $-1$。

   复数除了可以用 $z = a + bi$ 这种坐标表示法，还可以使用更直观的模+辐角表示法，即三角表示法：$z = re^{i\theta}$。