线性空间
数学中空间是一个非空的集合,用符号 $V$ 表示,它的组成包括两个部分:元素 + 规则,任何操作以及推导都只能在规则的基础上进行。
1. 线性空间
是一种定义了加法和数乘这两种规则的空间,其中的元素是向量,故也称为向量空间。符号 $P$ 表示一个数域。
1)加法运算:即当向量 $a,b\in V$,有唯一的和 $a+b\in V$ (封闭性),且加法运算满足以下性质:
a. $a + b = b + a$
b. $a + (b + c) = (a + b) + c$
c. 存在零元素 $0$,使得 $a + 0 = a$
d. 存在负元素 $-a$,使 $a + (-a) = 0$
以上的性质都是针对空间内的元素,即定义了向量的加法操作。
2)数乘运算(数量乘积):当 $a \in V,k,l \in P$ 时,有唯一的积 $ka \in V$ (封闭性),且乘法运算满足以下性质:
a. $k(a + b) = ka + kb$
b. $(k + l)a = ka + la$
c. $k(la) = (kl)a$
d. 数域中存在元素 1,$1 \cdot a = a$
空间是定义在数域上的,以上性质定义了数域 $P$ 内的元素(数)和向量相乘所允许的操作。
满足了以上几条性质,则称 $V$ 是定义在数域 $P$ 上的线性空间或向量空间。对于不同的数域,可能构成不同的线性空间。
之所以称为线性空间是由于所定义的加法和数乘运算都是线性运算。
向量的维度:向量坐标分量的个数。同一个线性空间中的向量必然都具有相同的维度,不然元素之间就无法进行加减。
线性空间的维度:空间的所有元素中,构成线性无关的向量的最大个数,即极大线性无关组的向量个数。
线性空间的维度不一定等于它里面所含向量的维度。关键在于空间里面的元素是哪些,比如:
1)所有三维向量可以构成一个线性空间,很明显这个线性空间的维度也是 $3$。
2)如图,位于下图斜面上的向量,用三个坐标来描述,即向量是三维的,斜面上的向量全体也可以构成一个线性空间,但此时向量
空间的维度是 $2$,即只需要两个线性无关的向量 $v_{1},v_{2}$ 就可以表示该空间中的所有元素。
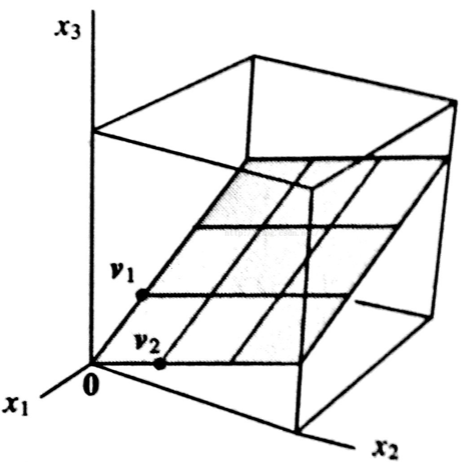
总结:向量空间的维度,取决于里面包含了哪些向量,里面的向量必定都有相同的分量个数。
2. 内积空间
向量空间中增加了一个额外的结构,这个额外的结构叫做内积(点积),这时的空间称为内积空间。
这个增添的结构将一对矢量与一个纯量连接起来,允许我们严格地谈论矢量的夹角和长度,并进一步谈论矢量的正交性。
两个向量 $a = (x_{1},x_{2},...,x_{n})$ 和 $b = (y_{1},y_{2},...,y_{n})$ 的内积定义为
$$a \cdot b = (a,b) = a \cdot b = x_{1}y_{1} + x_{2}y_{2} +...+ x_{n}y_{n} = \sum_{i=1}^{n}x_{i}y_{i}$$
$\bullet$ 两个向量的内积具有如下性质:
1)$(a,b) = (b,a)$
2)$(ka,b) = k(a,b)$
3)$(a+b,c) = (a,c) + (b,c)$
$\bullet$ 根据内积可以引出向量长度的定义:$|a| = \sqrt{(x,x)}$。关于向量长度的基本性质:
1)非负性:对内积空间中的任一个向量 $a$,有 $|a| \geq 0$。当向量 $a = 0$时,$|a|=0$。
2)齐次性:对任意的 $k \in P$,有 $|ka| = |k||a|$。
3)三角不等式:$|a+b| \leq |a| + |b|$。
$\bullet$ 上面是点积的坐标定义,它也有个几何定义:
$$a \cdot b = |a||b|\cos \theta$$
其中 $|b|\cos \theta$ 为向量 $b$ 在向量 $a$ 上的投影。
更通俗来讲:向量内积计算的是一个向量乘以另一个向量在该向量上的正交投影。因此也就是把另一个向量作分解,只有平行部分才有作用。
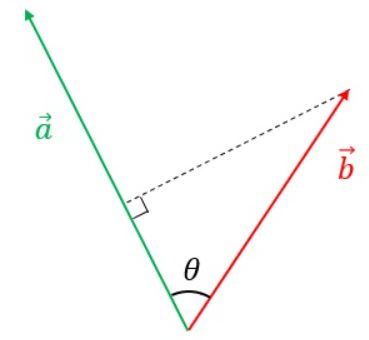
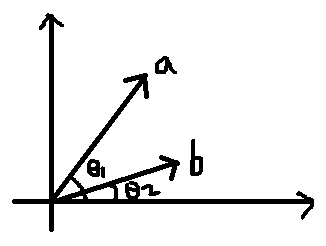
向量内积的坐标定义和几何定义两者有什么联系呢?为什么它们的值是一样的?
向量的几何定义可以从坐标定义推导出来,如上右图,可知
$$a \cdot b = a_{x}b_{x} + a_{y}b_{y} = |a|\cos \theta_{1} \cdot |b|\cos \theta_{2} + |a|\sin \theta_{1} \cdot |b|\sin \theta_{2} \\
= |a||b|(\cos \theta_{1}\cos \theta_{2} + \sin \theta_{1}\sin \theta_{2}) \\
= |a||b|\cos (\theta_{1} - \theta_{2})$$
是不是很神奇,向量内积的几何定义告诉我们,不管两个相同向量在哪一个参考系中,它们的内积都是一样的,只和它们的模和角度有关。
最简单的建立坐标系的方法就是以其中某一个向量作为坐标轴。
内积数值上我们可以看出两个向量的在方向上的接近程度。当内积值为正值时,两个向量大致指向相同的方向(方向夹角小于90度);
当内积值为负值时,两个向量大致指向相反的方向(方向角大于90度);当内积值为0时,两个向量互相垂直。
3. 赋范线性空间
一般的线性空间是没有定义内积的,也就没有向量长度的概念,引入向量范数就是为了在一般的线性空间中建立类似向量长度的这种度量。
设 $V$ 是实数域 $R$ 上的 $n$ 维线性空间,对于 $V$ 中的任意一个向量 $a$,按照某一个确定的法则 $f(a)$ 对应一个实数,这个实数称为 $a$ 的
范数,记为 $||a||$,并且要求满足以下 3 个条件:
1)非负性:对内积空间中的任一个向量 $a$,当 $a \neq 0$ 时,有 $||a|| \geq 0$。当向量 $a = 0$ 时,$||a||=0$。
2)齐次性:对任意的 $k \in P$,有 $||ka|| = |k| \cdot ||a||$。
3)三角不等式:$||a+b|| \leq ||a|| + ||b||$。
定义了范数的空间称为赋范线性空间。
对同一个向量 $a$,不同的法则 $f(a)$ 会计算出不同的范数,向量的长度就是一种范数。
- 关于向量范数,具有以下基本性质:
1)$||0|| = 0,||-a|| = ||a||$
2)当 $a \neq 0$,有 $||\frac{a}{||a||}|| = 1$
3)$| ||a|| - ||b|| | \leq || a - b ||$
- 下面介绍几种常用的向量范数:
设向量 $a = \left \{ x_{1},x_{2},...,x_{n} \right \}$,$b = \left \{ y_{1},y_{2},...,y_{n} \right \}$。
1)$L1$ 范数:向量 $a$ 的各个元素绝对值之和,即
$$||a||_{1} = \sum_{i=1}^{n}|x_{i}|$$
证明:验证它满足向量范数的 3 个条件即可。
i:非负性。$a \neq 0$ 时,至少有一个分量不为 $0$,所以向量各个分量的绝对值求和必大于 $0$。当 $a = 0$ 时,明显各个分量的绝对值和为 $0$。
ii:齐次性。
$$||ka||_{1} = \sum_{i=1}^{n}|kx_{i}| = \sum_{i=1}^{n}|k|\cdot |x_{i}| = |k| \sum_{i=1}^{n} |x_{i}| = |k|\cdot ||a||_{1}$$
iii:三角不等式。
$$||a+b||_{1} = \sum_{i=1}^{n}|x_{i} + y_{i}| \leq \sum_{i=1}^{n}(|x_{i}| + |y_{i}|) = \sum_{i=1}^{n}|x_{i}| + \sum_{i=1}^{n}y_{i}| = ||a||_{1} + ||b||_{1}$$
2)$Lp$ 范数:当 $1\leq p < +\infty$,向量 $a$ 的各个元素 $p$ 方和的 $1/p$ 次方,即
$$||a||_{p} = \left ( \sum_{i=1}^{n}|x_{i}|^{p} \right )^{\frac{1}{p}}$$
证明:验证它满足向量范数的 3 个条件即可。
i:非负性。可类比 $L1$ 范数,这里不再赘述。
ii:齐次性。
$$||ka||_{p} =\left ( \sum_{i=1}^{n}|kx_{i}|^{p} \right )^{\frac{1}{p}} = |k|\cdot \left ( \sum_{i=1}^{n} |x_{i}|^{p} \right )^{\frac{1}{p}} = |k|\cdot ||a||_{p}$$
iii:三角不等式。由闵可夫斯基不等式直接得
$$||a+b||_{p} = \left \{ \sum_{i=1}^{n}(x_{i} + y_{i})^{p} \right \}^{\frac{1}{p}} \leq \left ( \sum_{i=1}^{n}|x_{i}|^{p} \right )^{\frac{1}{p}} + \left ( \sum_{i=1}^{n}|y_{i}|^{p} \right )^{\frac{1}{p}} = ||a||_{p} + ||b||_{p}$$



