二重积分
设函数 $z = f(x,y)$ 在有界闭区域 $D$ 上有界,将 $D$ 任意分成 $n$ 个小闭区域 $\Delta \sigma _{i},i=1,2,3,...,n$,$\Delta \sigma _{i}$ 表示第 $i$ 个子区域的面积,
在 $\Delta \sigma _{i}$ 上任取一点 $(\xi_{i},\eta_{i})$,做和
$$\sum_{i=1}^{n}f(\xi _{i},\eta _{i})\Delta \sigma _{i}$$
记 $\lambda$ 为 $n$ 个小区域的最大直径。
当分割越来越“精细”的时候,即 $\lambda \rightarrow 0,n\rightarrow +\infty$,分割后的子区域围成的图形就接近长方体,考虑式子
$$\lim_{\lambda \rightarrow 0}\sum_{i=1}^{n}f(\xi _{i},\eta _{i})\Delta \sigma _{i}$$
如果这个极限存在,且该极限值与区域 $D$ 的分法及 $(\xi_{i},\eta_{i})$ 的取法无关,则称此极限为函数 $f(x,y)$ 在区域 $D$ 上的二重积分,记为
$$\iint_{D}^{}f\left ( x,y \right )d\sigma = \lim_{\lambda \rightarrow 0}\sum_{i=1}^{n}f(\xi _{i},\eta _{i})\Delta \sigma _{i} = \sum_{i=1}^{+\infty}f(\xi _{i},\eta _{i})\Delta \sigma _{i}$$
$\bullet$ 积分形式和累加形式做一个比较:
1)$d\sigma$ 和 $\Delta \sigma$ 都是无穷小量,且都是标量,表示小闭区域的面积,无限趋于 0。$d\sigma = dxdy$,$dx$ 和 $dy$ 是被分割后小闭区域的长和宽,都是标量,
乘积就是物理意义上的面积。
2)$x$ 和 $y$ 是积分变量,相当于 $\xi$ 和 $\eta$。$D$ 无穷分割后,在每个小长方体的底面上可以任取一点,用以计算对应函数值 $f(x,y)$。极限情况下,
$(x,y)$ 取遍 $D$ 内的每一个点,所以通过 $x$ 和 $y$ 或 $\xi$ 和 $\eta$ 可以确定积分区域。
3)符号 $\iint_{D}^{}$ 表示在区域 $D$ 上极限求和,它不仅表示无穷项求和,还限定了积分区域,不同于定积分,二重积分只能够正向积分,即积分下限必须
小于积分上限。而 $\lim_{\lambda \rightarrow 0}\sum_{i=1}^{n} = \lim_{\lambda \rightarrow 0}\sum_{i=1}^{\infty}$ 只是表示量级是无穷项累加,并不知道是哪个区域。
$\bullet$ 二重积分的几何意义:若 $\iint_{D}^{}f\left ( x,y \right )d\sigma$ 存在,因为积分区间只能是正向的,所以只需考虑被积函数 $f(x,y)$ 的正负。当 $f(x,y)\geq 0$ 时,
积分值是以 $D$ 为底,以曲面 $z = f(x,y)$ 为顶的曲顶柱体的体积。
$\bullet$ 二重积分的计算:需要转化为定积分进行计算。
$$\iint_{D}^{}f\left ( x,y \right )d\sigma = \iint_{D}^{}f\left ( x,y \right )dxdy = \iint_{D}^{}f\left ( x,y \right )dydx$$
我们需要确定积分变量 $x$ 和 $y$ 各自的积分区间,换句话说,即确定 $x$ 和 $y$ 各自的约束条件,使其能构成区域 $D$,然后确定积分的先后顺序。
需要注意的是,先积分的变量(如先对 $x$ 积分)积分完成后,该变量就不存在了,第二次积分的被积函数只是关于 $y$ 的函数,所以
a. 先积分的变量的积分限是关于另一个积分变量的函数,即该坐标正方向上边界曲线函数。
b. 后积分变量的积分限是不含任何积分变量的常量,是边界最值,不然二重积分的结果就含有积分变量了。
下面进一步讲述如何确定积分限:无论是哪个坐标系,对谁积分,就向它的正方向画线,得到线所穿过的边界曲线函数或边界最值。
1)利用直角坐标系计算
a. 先 $y$ 后 $x$
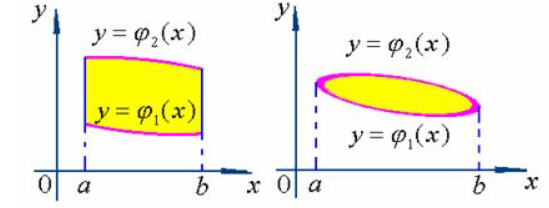
i. 往 $y$ 轴正方向画条线,穿过边界曲线 $y = \varphi _{1}(x),y = \varphi _{2}(x)$。
ii. 往 $x$ 轴正方向画条线,确定坐标左右界(最值),即两个常数 $x = a,x = b$。
$$\iint_{D}^{}f(x,y)dxdy = \int_{a}^{b}\int_{\varphi _{1}(x)}^{\varphi _{2}(x)}f(x,y)dxdy = \int_{a}^{b}[\int_{\varphi _{1}(x)}^{\varphi _{2}(x)}f(x,y)dy]dx = \int_{a}^{b}dx\int_{\varphi _{1}(x)}^{\varphi _{2}(x)}f(x,y)dy$$
b. 先 $x$ 后 $y$

i. 往 $x$ 轴正方向画条线,穿过边界曲线 $x = \phi _{1}(y),x = \phi _{2}(y)$。
ii. 往 $y$ 轴正方向画条线,确定坐标上下界(最值),即两个常数 $y = c,y = d$。
$$\iint_{D}^{}f(x,y)dxdy = \int_{c}^{d}\int_{\phi_{1}(y)}^{\phi_{2}(y)}f(x,y)dxdy = \int_{c}^{d}[\int_{\phi _{1}(y)}^{\phi _{2}(y)}f(x,y)dx]dy = \int_{c}^{d}dy\int_{\phi _{1}(y)}^{\phi _{2}(y)}f(x,y)dx$$
2)利用极坐标计算
极坐标方法一般采用先 $\rho$ 后 $\theta$ 顺序进行积分。

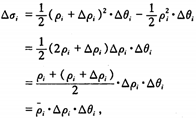
i. 从极点开始画射线,穿过边界曲线 $\rho = \rho _{1}(\theta ), \rho = \rho _{2}(\theta )$。
ii. 往逆时针方向画圆弧线,确定角度的边界(最值),即$\theta =\alpha ,\theta =\beta $。
$$\iint_{D}^{}f(x,y)dxdy = \int_{\alpha }^{\beta }\int_{\rho _{1}(\theta )}^{\rho _{2}(\theta )}f(\rho cos\theta ,\rho sin\theta )\rho d\rho d\theta = \int_{\alpha }^{\beta }d\theta\int_{\rho _{1}(\theta )}^{\rho _{2}(\theta )}f(\rho cos\theta ,\rho sin\theta )\rho d\rho$$


