有向图查找长度为3~7的所有环
算法目标:在一个有向图中寻找出所有长度在3到7之间的环,环的数量可达百万级。
数据结构定义:
#define maxID 200000 vector<int> Vout[maxID]; // 存储每个结点出边所连的所有结点。Vout[i].size()即为所有的出度 vector<int> Vin[maxID]; // 存储每个结点入边所连的所有结点。Vin[i].size()即为所有的入度 vector<int> ans; // 存储构成环的所有结果路径 vector<int> tmpPath; bool vis[maxID];
1. 基本思路:
对图中的每个结点做深度为7的DFS搜索,保存符合条件的每个环。注意这里要搜索的是全部路径,而不是单单遍历图中的所有点,所以需要回溯。
在栈返回上一层时,得清空结点标记并弹出结点。
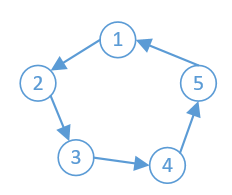
这里有一个问题,比如下图,对节点1搜索时,能够找到环1->2->3->4->5,对结点2搜索时,能够找到环2->3->4->5->1。
故为了避免搜索到重复的环,需要做一些约定:一个环的起始结点id最小。
void dfs7(int head, int cur, int depth)
{
vis[cur] = true;
tmpPath.push_back(start);
for(int i = 0; i < Vout[cur].size(); ++i) // 遍历所有的出边
{
int v = Vout[cur][i];
if(v < head || vis[v]) continue;
// 环的判定条件: Vout[cur]的孩子结点v为起始点head
if (v == head && depth >= 3)
{
ans.push_back(tmpPath); // 得到一条结果
}
if (depth < 7) // 继续搜索
{
dfs7(head, v, depth + 1);
}
}
vis[cur] = false;
tmpPath.pop_back();
}
void search()
{
for (int i = 0; i < N; ++i)
{
if (Vout[i].size() && Vin[i].size()) // 只有出入度不为0的结点才会构成环
{
dfs7(i, i, 1);
}
}
}
说明:对每个结点都做深度为7的搜索,当每个结点的出度很多时,每多遍历一层,所搜索的路径将成倍增长,导致复杂度很高。
2. 6+1优化思路
对结点head进行遍历前,先标记head的所有入边,这样当我们递归进入head的第6层时,直接根据这个标记数组判断其孩子结点是不是head的入边结点。
省去了对第七层的搜索。新增加一个数组vis2,若结点k为head的入边结点,则令vis2[k] = head + 1; 这样做标记的目的是省去每次memset重新初始化
vis2数组的时间,标记为head + 1,是因为有id为0的结点。代码如下:
int vis2[MAXID]; // 标记入边结点
void search()
{
for (int i = 0; i < N; ++i)
{
if (Vout[i].size() && Vin[i].size()) // 只有出入度不为0的结点才会构成环
{
// 先标记入边结点
for(int j = 0; j < Vin[i].size(); ++j)
{
int v = Vin[i][j];
vis2[v] = i + 1; // 标记
}
dfs6(i, i, 1);
}
}
}
void dfs6(int head, int cur, int depth)
{
vis[cur] = true;
tmpPath.push_back(start);
for(int i = 0; i < Vout[cur].size(); ++i) // 遍历所有的出边
{
int v = Vout[cur][i];
if(v < head || vis[v]) continue;
// 环的判定条件: v走一步可到达head
if (vis2[v] == head + 1 && depth >= 2)
{
tmpPath.push_back(v); // 该孩子结点还未放入临时数组
ans.push_back(tmpPath); // 得到一条结果
tmpPath.pop_back();
}
if (depth < 6) // 继续搜索
{
dfs6(head, v, depth + 1);
}
}
vis[cur] = false;
tmpPath.pop_back();
}
3. 5+2优化思路
反向遍历两层,保存所有符合条件,且走两步能到达head的路径,并标记起始结点。
标记使用vis2数组,存储使用rPath2结构。具体代码如下:
std::vector<int> rPath2[MAXID]; // 反向存储两层路径
int vis2[MAXID]; // 标记走两步可到达head的结点
void search()
{
for (int i = 0; i < N; ++i)
{
if (Vout[i].size() && Vin[i].size()) // 只有出入度不为0的结点才会构成环
{
rdfs2(i, i, 1)
dfs5(i, i, 1);
}
}
}
void rdfs2(int head, int cur, int depth)
{
vis[cur] = true;
for(int i = 0; i < Vin[cur].size(); ++i)
{
int v = Vin[cur][i];
if(v < head || vis[v]) continue;
if (depth == 2)
{
if(vis2[v] != head + 1)
{
rPath2[v].clear();
}
vis2[v] = head + 1;
rPath2[v].push_back(cur);
}
if (depth < 2)
{
rdfs2(head, v, depth + 1);
}
}
vis[cur] = false;
}
void dfs5(int head, int cur, int depth)
{
vis[cur] = true;
tmpPath.push_back(start);
for(int i = 0; i < Vout[cur].size(); ++i) // 遍历所有的出边
{
int v = Vout[cur][i];
if(v < head || vis[v]) continue;
// 环的判定条件: v结点走两步可到达head
if (vis2[v] == head + 1)
{
tmpPath.push_back(v); // 该孩子结点放入临时数组
for(int j = 0; j < rPath2[v].size(); ++j)
{
int c = rPath2[v][j];
if(vis[c]) continue;
tmpPath.push_back(c); // 孩子结点的孩子结点放入临时数组
ans.push_back(tmpPath); // 得到一条结果
tmpPath.pop_back();
}
tmpPath.pop_back();
}
if (depth < 5) // 继续搜索
{
dfs5(head, v, depth + 1);
}
}
vis[cur] = false;
tmpPath.pop_back();
}
4. 通过距离进行剪枝
反向遍历3层: 如果将图看作是无向图,一个点数为7的环中,距离起点最远的点距离不超过3。
引入vis1数组对反向距离不超过3的结点进行标记。具体代码如下:
std::vector<int> rPath2[MAXID]; // 反向存储两层路径
int vis1[MAXID]; // 标记反向距离不超过3的所有结点
int vis2[MAXID]; // 标记走两步可到达head的结点
void search()
{
for (int i = 0; i < N; ++i)
{
if (Vout[i].size() && Vin[i].size()) // 只有出入度不为0的结点才会构成环
{
rdfs3(i, i, 1)
dfs5(i, i, 1);
}
}
}
void rdfs3(int head, int cur, int depth)
{
vis[cur] = true;
for(int i = 0; i < Vin[cur].size(); ++i)
{
int v = Vin[cur][i];
if(v < head || vis[v]) continue;
vis1[v] = head + 1;
if (depth == 2)
{
if(vis2[v] != head + 1)
{
rPath2[v].clear();
}
vis2[v] = head + 1;
rPath2[v].push_back(cur);
}
if (depth < 3)
{
rdfs3(head, v, depth + 1);
}
}
vis[cur] = false;
}
void dfs5(int head, int cur, int depth)
{
vis[cur] = true;
tmpPath.push_back(start);
for(int i = 0; i < Vout[cur].size(); ++i) // 遍历所有的出边
{
int v = Vout[cur][i];
if(v < head || vis[v]) continue;
if (depth > 3 && vis1[v] != head + 1) continue; // 交集才访问
// 环的判定条件: v结点走两步可到达head
if (vis2[v] == head + 1)
{
tmpPath.push_back(v); // 该孩子结点放入临时数组
for(int j = 0; j < rPath2[v].size(); ++j)
{
int c = rPath2[v][j];
if(vis[c]) continue;
tmpPath.push_back(c); // 孩子结点的孩子结点放入临时数组
ans.push_back(tmpPath); // 得到一条结果
tmpPath.pop_back();
}
tmpPath.pop_back();
}
if (depth < 5) // 继续搜索
{
dfs5(head, v, depth + 1);
}
}
vis[cur] = false;
tmpPath.pop_back();
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号