单源最短路径算法之Dijkstra

算法描述：

    Dijkstra解决的是带权重的有向图上单源最短路径问题，该算法要求所有边的权重都为非负值。

    算法在运行过程中维持的关键信息是一组结点集合S，从源点s到该集合中每个结点之间的最短路径都已经被找到。

    算法重复从结点集V-S中选择最短路径估计最小的结点u，将u加入到集合S，然后对所有从u出发的边进行松弛。

 

算法实现：

dist数组记录源点到图中结点的最短距离，初始均为无穷大，置dist[start] = 0供算法启动。

在结点u加入集合S中时，这条路径中u的前驱一定已经在集合S内了。

int edge[N][N];

int dist[N];  // 最短距离
int bset[N];  // 标记是否已在集合S
int pre[N];   // 记录前驱

const int INF = 999999999;

void Dijkstra(start)
{
    fill(dist, dist + N, INF);
    fill(bset, bset + N, 0);

    dist[start] = 0;

    for(int i = 0; i < N; i++)
    {
        int min = INF;
        int u = -1;

        for(int j = 0; j < N; j++)
        {
            if(bset[j] == 0 && dist[j] < min) 
            {
                u = j;
                min = dist[j];
            }
        }

        if(u == -1) continue;
        bset[u] = 1;

        for(int j = 0; j < N; j++)
        {
            if(bset[j] == 0)
            {
                // 松弛操作
                if(dist[u] + edge[u][j] < dist[j])
                {
                    dist[j] = dist[u] + edge[u][j];
                    pre[j] = u;
                }
                else if(dist[u] + edge[u][j] == dist[j])
                {
                    // 说明到达该节点有多条最短路径
                }
            }
        }
    }
}

下面是一个python的实现：

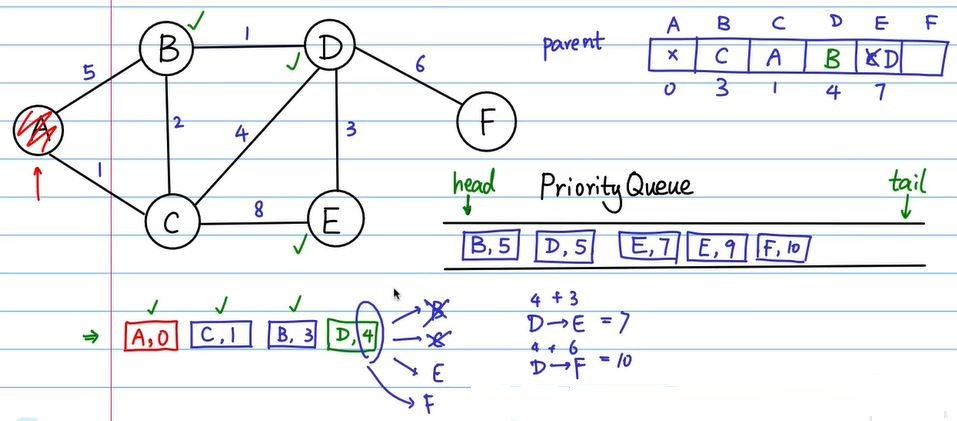
import heapq
import math

graph = {
    "A": {"B": 5, "C": 1},
    "B": {"A": 5, "C": 2, "D": 1},
    "C": {"A": 1, "B": 2, "D": 4, "E": 8},
    "D": {"B": 1, "C": 4, "E": 3, "F": 6},
    "E": {"C": 8, "D": 3},
    "F": {"D": 6}
}

def InitDistance(graph, s):
    distance = {s: 0}

    for vertex in graph:
        if vertex != s:
            distance[vertex] = math.inf
    return distance

def Dijkstra(graph, s):
    pqueue = []
    seen = set()
    parent = {s: None}
    distance = {s: 0}
    distance = InitDistance(graph, s)

    heapq.heappush(pqueue, (0, s))

    while (len(pqueue) > 0):
        pair = heapq.heappop(pqueue)
        dist = pair[0]
        vertex = pair[1]
        nodes = graph[vertex].keys()

        seen.add(vertex)

        for w in nodes:
            if w not in seen:
                if dist + graph[vertex][w] < distance[w]:
                    heapq.heappush(pqueue, (dist + graph[vertex][w], w))
                    parent[w] = vertex
                    distance[w] = dist + graph[vertex][w]
    return parent, distance

 

算法正确性证明：

    在带权重的有向图G=(V,E)中，初始时 S 为空集。

    我们需要证明的是：对于每次加入集合S的结点u来说，s到u的距离为最短距离。

    记 u.d 为 s 到 u 的距离，δ(s,u) 为 s 到 u 的最短距离，即证明：

         对于每次加入集合S的结点u来说，u.d = δ(s,u)

    这里使用反证法证明：

        假设：结点 u 是第一个加入到集合 S 时使得 u.d ≠ δ(s,u) 的结点

        源结点 s 是第一个加入到集合 S 中的结点，并且 s.d = δ(s,s) = 0, 结点 u 必定与结点 s 不同，即 u ≠ s。

        根据算法可知，当 u 加入到 S 时，一定存在某条从结点 s 到 u 的路径，并且 u 的前驱结点在集合S内，该路径记为 P1。

        由假设可知，还存在一条从 s 到 u 的最短路径，这条路径中 u 的前驱一定不在集合 S 中(不然松弛过程就会发现该路径)，该路径记为 P2。

        P2 路径中 u 的前驱为 b，b不在 S 内。

        

        因为 P2 < P1, 可推出 dist[b] < dist[u]，所以 b 会先于 u 进入，产生矛盾。