平衡二叉树
AVL树说明:
该树是一种高度平衡的二叉搜索树,该树中的每一个结点左右子树的高度至多相差1。
AVL树本身也是一个二叉搜索树。
AVL基本结构定义如下:
#define LH +1 // 左高
#define EH 0 // 等高
#define RH -1 // 右高
struct BTNode
{
int data;
int bf;
struct BTNode *lchild;
struct BTNode *rchild;
};
斐波那契数列:
1、1、2、3、5、8、13、21、34、……
其递推式定义为:F(1) = 1, F(2) = 1, F(n) = F(n-1) + F(n-2) (n>=3)
即斐波那契数列的第1、第2项都为1,然后后面的每一项都是前两项之和。
平衡二叉树最少结点计算:
完全二叉树是平衡二叉树最“完全”的状态。
那满足平衡二叉树的最不完全的状态,即结点最少的状态是怎样的?
树高度记为h,树中结点总数记为C,结点内的值代表平衡因子,则:
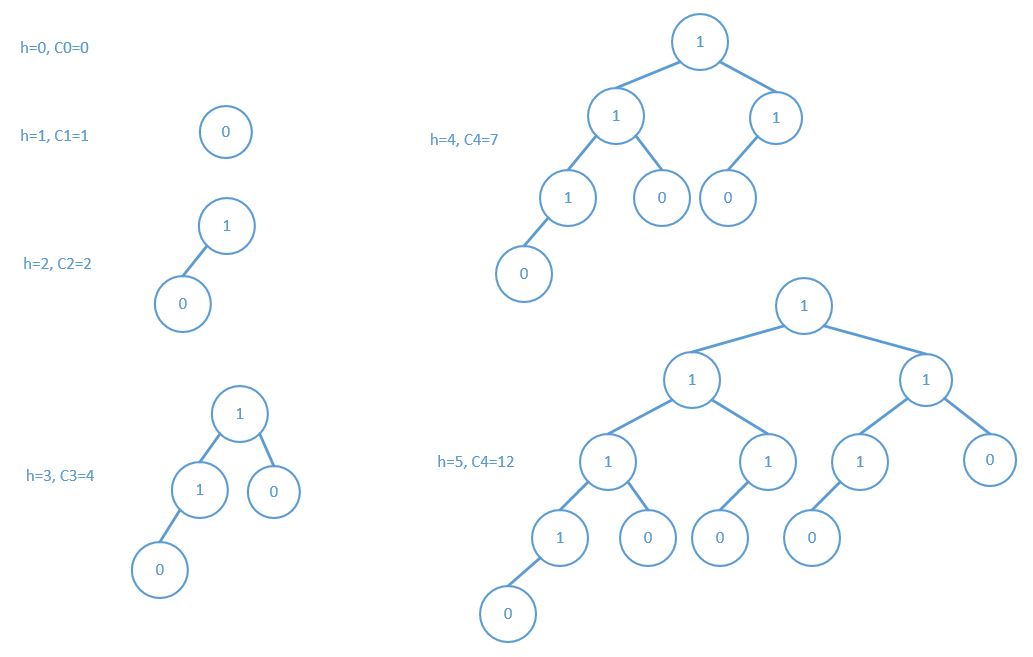
高度为h的平衡二叉树的最少结点总数为Ch = Ch-1 + Ch-2 + 1
和斐波那契数列对比:
Fh 1 1 2 3 5 8 13 21 34
Ch 1 2 4 7 12 20 33
所以Ch = F(n+2) - 1
如何画出上面的图:每次增加一个最左结点导致高度加1,然后需要补充一些结点,在原来树中度为0的结点下增加一个左孩子,度为1的
结点下增加一个右孩子即可。
AVL树旋转详解
若某节点A出现失衡,即左子树或右子树长高了,导致左右子树的高度差2,会有以下四种情况:
- 该点左子树比右子树高度高2,因为原来是平衡的,所以新结点一定是左孩子的孩子结点
1. 在左孩子的左子树上插入结点
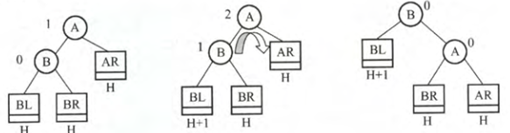
由于是左子树增高,所以左孩子B结点一定存在,其余抽象,BL,BR,AR的高度均是H,否则无法导致插入后A点失衡。
插入新结点后,BL这棵树高度加1。
需要进行右旋,对比上图可得如下代码:
void R_Rotate(BTNode *&A)
{
BTNode *B= A->lchild;
A->lchild = B->rchild;
B->rchild = A;
A = B;
}
插入到左子树的左孩子整体的平衡调整代码如下:
A->bf = EH;
B->bf = EH;
R_Rotate(A);
2. 在左孩子的右子树上插入结点
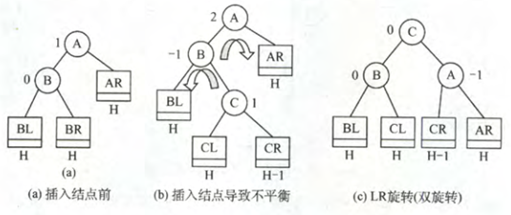
结点插入在BR上这棵树上,BR树高度变为H+1,将BR树变成b图所示形式,必存在一个C结点,其左右子树高度差1,
b图画的是CL比CR高,当然也可能是CR比CL高,调整平衡因子的时候需要做判断。
插入到左孩子的右子树导致的失衡,应该先左旋再右旋,代码如下:
BTNode *B = A->lchild;
BTNode *C = B->rchild;
switch (C->bf)
{
case LH: // CL高度H, CR高度H-1
A->bf = RH;
B->bf = EH;
break;
case EH: // CL高度H, CR高度H
A->bf = EH;
B->bf = EH;
break;
case RH: // CL高度H-1, CR高度H
A->bf = EH;
B->bf = LH;
break;
}
C->bf = EH;
L_Rotate(B);
R_Rotate(A); // 右旋代码见下
- 该点右子树比左子树高度高2,因为原来是平衡的,所以新结点一定是右孩子的孩子结点
1. 在右孩子的右子树上插入结点
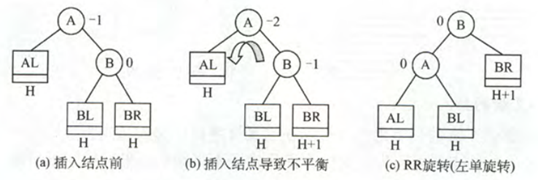
需要进行左旋,对比上图可得如下代码:
void L_Rotate(BTNode *&A)
{
BTNode *B = A->rchild;
A->rchild = B->lchild;
B->lchild = A;
A = B;
}
插入到右子树的右孩子整体的平衡调整代码如下:
A->bf = EH;
B->bf = EH;
L_Rotate(A);
2. 在右孩子的左子树上插入结点
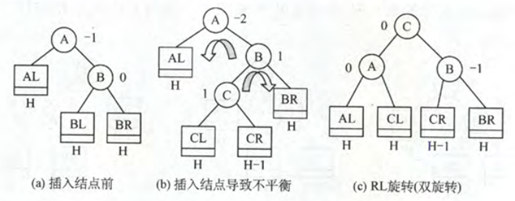
插入到右孩子的右子树导致的失衡,应该先右旋再左旋,代码如下:
BTNode *B = A->rchild;
BTNode *C = B->lchild;
switch (C->bf)
{
case LH: // CL高度H, CR高度H-1
A->bf = EH;
B->bf = RH;
break;
case EH: // CL高度H, CR高度H
A->bf = EH;
B->bf = EH;
break;
case RH: // CL高度H-1, CR高度H
A->bf = LH;
B->bf = EH;
break;
}
C->bf = EH;
R_Rotate(B);
L_Rotate(A);
算法实现:
层层递归到栈底,插入一个结点后,返回到栈上一层,taller置为true,然后判断是否该旋转该结点并修改平衡因子,判断是否增高,再返回栈上一层。。。。
void LeftBalance(BTNode *&A)
{
BTNode *C = A->lchild;
switch (C->bf)
{
case LH:
A->bf = EH;
B->bf = EH;
R_Rotate(A);
break;
case RH:
BTNode *B = C->rchild;
switch (B->bf)
{
case LH:
A->bf = RH;
C->bf = EH;
break;
case EH:
A->bf = EH;
C->bf = EH;
break;
case RH:
A->bf = EH;
C->bf = LH;
break;
}
B->bf = EH;
L_Rotate(C);
R_Rotate(A);
break;
}
}
void RightBalance(BTNode *&A)
{
BTNode *B = A->rchild;
switch (B->bf)
{
case RH:
A->bf = EH;
B->bf = EH;
L_Rotate(A);
break;
case LH:
BTNode *C = B->lchild;
switch (C->bf)
{
case LH:
A->bf = EH;
B->bf = RH;
break;
case EH:
A->bf = EH;
B->bf = EH;
break;
case RH:
A->bf = LH;
B->bf = EH;
break;
}
C->bf = EH;
R_Rotate(B);
L_Rotate(A);
break;
}
}
int InsertAVL(BTNode *&t, int e, int &taller)
{
if (t == NULL)
{
t = (BTNode*)malloc(sizeof(BTNode));
t->data = e;
t->lchild = NULL;
t->rchild = NULL;
t->bf = EH;
taller = true;
}
else
{
if (t->data == e)
{
taller = false;
return false;
}
else if(t->data > e)
{
if (InsertAVL(t->lchild, e, taller) == false)
return false;
// e插入到左子树,且左子树长高
if (taller)
{
// 判断结点原来的平衡因子
switch(t->bf)
{
case LH:
LeftBalance(t);
taller = false;
break;
case EH:
t->bf = LH;
taller = true;
break;
case RH:
t->bf = EH;
taller = false;
break;
}
}
}
else
{
if (InsertAVL(t->rchild, e, taller) == false)
return false;
// e插入到右子树,且右子树长高
if(taller)
{
// 判断结点原来的平衡因子
switch(t->bf)
{
case LH:
t->bf = EH;
taller = false;
break;
case EH:
t->bf = RH;
taller = true;
break;
case RH:
RightBalance(t);
taller = false;
break;
}
}
}
}
return true;
}
平衡二叉树的另一种实现:
#define HIGHER 1
#define LOWER -1
#define EQUAL 0
struct TreeNode
{
struct TreeNode *pLeft;
struct TreeNode *pRight;
void *pData;
int diff; // 代表: 右子树高度 - 左子树高度
};
TreeNode* MallocNode()
{
TreeNode *pTemp;
pTemp = (TreeNode *)malloc(sizeof(TreeNode));
if(pTemp == NULL) return NULL;
pTemp->pLeft = NULL;
pTemp->pRight = NULL;
pTemp->pData = NULL;
pTemp->diff = 0;
return pTemp;
}
void AdjustTree(TreeNode *&pHead)
{
TreeNode *pTemp, *pPre,*pCur;
switch(pHead->diff)
{
case 2: // 右子树比左子树高 2
pPre = pHead;
pCur = pPre->pRight;
if(pCur->diff == -1) // 先右旋再左旋
{
pTemp = pCur->pLeft;
switch(pTemp->diff)
{
case 0:
pPre->diff = 0;
pCur->diff = 0;
break;
case 1:
pPre->diff = -1;
pCur->diff = 0;
break;
default:
pPre->diff = 0;
pCur->diff = 1;
break;
}
pPre->pRight = pTemp->pLeft;
pCur->pLeft = pTemp->pRight;
pTemp->pLeft = pPre;
pTemp->pRight = pCur;
pTemp->diff = 0;
pHead = pTemp;
}
else // 左旋
{
pPre->pRight = pCur->pLeft;
pCur->pLeft = pPre;
pPre->diff = 1 - pCur->diff;
pCur->diff--;
pHead = pCur;
}
break;
case -2: // 左子树比右子树高 2
pPre = pHead;
pCur = pPre->pLeft;
if(pCur->diff == 1) // 先左旋再右旋
{
pTemp = pCur->pRight;
switch(pTemp->diff)
{
case 0:
pPre->diff = 0;
pCur->diff = 0;
break;
case 1:
pPre->diff = 0;
pCur->diff = -1;
break;
default:
pPre->diff = 1;
pCur->diff = 0;
break;
}
pCur->pRight = pTemp->pLeft;
pPre->pLeft = pTemp->pRight;
pTemp->pLeft = pCur;
pTemp->pRight = pPre;
pTemp->diff = 0;
pHead = pTemp;
}
else // 右旋
{
pPre->pLeft = pCur->pRight;
pCur->pRight = pPre;
pPre->diff = -1 - pCur->diff;
pCur->diff++;
pHead = pCur;
}
break;
default:
break;
}
}
/*
pFunction: 实现结点值的对比
pAssign: 实现了结点值的赋值
上面两个函数需要根据结点值的具体类型进行实现,这里没有实现。
*/
int InsertTree(TreeNode *&pHead, void *pValue, int (*pFunction)(void *, void *), void (*pAssign)(void **, void *))
{
int diff, res, r;
TreeNode *pTemp;
if(pHead == NULL)
{
pTemp = MallocNode();
if(pTemp == NULL) return -1;
(*pAssign)(&pTemp->pData, pValue);
pHead = pTemp;
return EQUAL;
}
diff = pHead->diff;
res = (*pFunction)(pValue, pHead->pData);
if(res == 0)
{
(*pAssign)(&pHead->pData, pValue);
return EQUAL;
}
if(res > 0) /* right */
{
if(pHead->pRight != NULL)
{
r = InsertTree(pHead->pRight, pValue, pFunction, pAssign);
if(r < 0) return -1;
if(r == HIGHER) pHead->diff++;
}
else
{
if((pTemp = MallocNode()) == NULL)
{
printf("error mallocRight BinNode.\n");
return -1;
}
(*pAssign)(&pTemp->pData, pValue);
pHead->pRight = pTemp;
pHead->diff++; // 右子树增高
}
}
else /* left */
{
if(pHead->pLeft != NULL)
{
r = InsertTree(pHead->pLeft, pValue, pFunction, pAssign);
if(r < 0) return -1;
if(r == HIGHER) pHead->diff--;
}
else
{
if((pTemp = MallocNode()) == NULL)
{
printf("error mallocLeft BinNode.\n");
return -1;
}
(*pAssign)(&pTemp->pData, pValue);
pHead->pLeft = pTemp;
pHead->diff--; // 左子树增高
}
}
AdjustTree(pHead); // 进行平衡
// diff 是原来的平衡因子,原来为 0,现在非 0,意味着树长高了
if(diff == 0 && pHead->diff) return HIGHER;
return EQUAL;
}


