Lift, Splat, Shoot, LSS代码详尽分析与解读
LSS是英伟达在ECCV2020上发表的文章《Lift, Splat, Shoot: Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D》中提出的一个BEV感知算法,后续很多BEV感知算法如CaDDN、BEVDet都是在LSS的基础上实现的。本文将结合论文和代码详细解读LSS的原理。鸟瞰图BEV("bird's-eye-view")自动驾驶BEV感知范式的开山之作!
github:https://github.com/nv-tlabs/lift-splat-shoot
paper:https://arxiv.org/abs/2008.05711
数据层:
class SegmentationData(NuscData):
def __init__(self, *args, **kwargs):
super(SegmentationData, self).__init__(*args, **kwargs)
def __getitem__(self, index):
index = 16 #55(nice) #25
rec = self.ixes[index]
#从6个摄像头随机取5个
cams = self.choose_cams() #['CAM_FRONT_LEFT' 'CAM_FRONT_RIGHT' 'CAM_BACK_LEFT' 'CAM_BACK', 'CAM_BACK_RIGHT']
#imgs [5, 3, 128, 352]
#rots [5, 3, 3]
#trans [5, 3]
#intrins [5, 3, 3]
#post_rots[5, 3, 3]
#post_trans[5, 3]
imgs, rots, trans, intrins, post_rots, post_trans = self.get_image_data(rec, cams)
binimg = self.get_binimg(rec) #[1, 200, 200]
return imgs, rots, trans, intrins, post_rots, post_trans, binimg
def img_transform(img, post_rot, post_tran,
resize, resize_dims, crop,
flip, rotate):
# adjust image #[1600,900] -->> [354, 199]
img = img.resize(resize_dims)
img = img.crop(crop) #[354, 199] -->> [352, 128]
if flip:
img = img.transpose(method=Image.FLIP_LEFT_RIGHT)
img = img.rotate(rotate)
#post_rot [1, 0]
# post-homography transformation [0, 1]
post_rot *= resize
post_tran -= torch.Tensor(crop[:2]) #[0, 0]
if flip:
A = torch.Tensor([[-1, 0], [0, 1]])
b = torch.Tensor([crop[2] - crop[0], 0])
post_rot = A.matmul(post_rot)
post_tran = A.matmul(post_tran) + b
A = get_rot(rotate/180*np.pi) #[2, 2]
b = torch.Tensor([crop[2] - crop[0], crop[3] - crop[1]]) / 2
b = A.matmul(-b) + b
post_rot = A.matmul(post_rot)
post_tran = A.matmul(post_tran) + b
return img, post_rot, post_tran
https://zhuanlan.zhihu.com/p/608931944
这个链接讲解的比较好,转自该链接


img_transform这个函数主要是随机crop图像的,它是先resize再crop,还有flip、rot操作,同时记录了这些操作的矩阵post_rot、post_tran,为了后续点还原到原图。
def get_binimg(self, rec):
egopose = self.nusc.get('ego_pose',
self.nusc.get('sample_data', rec['data']['LIDAR_TOP'])['ego_pose_token'])
#egopose "translation" "rotation"存放的是全局坐标系,
trans = -np.array(egopose['translation']) #取负,是由全局转自车
rot = Quaternion(egopose['rotation']).inverse #取逆,是由全局转自车
img = np.zeros((self.nx[0], self.nx[1])) #[200, 200]
#cv2.circle(img, (self.nx[0]//2,self.nx[1]//2),2,1,2) #用圆点画出自车位置,方便观察
for tok in rec['anns']:
inst = self.nusc.get('sample_annotation', tok)
# add category for lyft
if not inst['category_name'].split('.')[0] == 'vehicle':
continue
box = Box(inst['translation'], inst['size'], Quaternion(inst['rotation']))
#调用nuscene给的方法(nuscenes/utils/data_classes.py)
box.translate(trans) #self.center += x
box.rotate(rot) #转到自车坐标系
pts = box.bottom_corners()[:2].T #8个角点取下面4个点,注意是在自车坐标系下
#self.bx[-49.75, -49.75, 0] self.dx[0.5, 0.5, 20]
#这里- self.bx[:2] + self.dx[:2]/2.是[50, 50]
#意思是把坐标系挪到右下角
pts = np.round(
(pts - self.bx[:2] + self.dx[:2]/2.) / self.dx[:2]
).astype(np.int32)
pts[:, [1, 0]] = pts[:, [0, 1]] #坐标系xy对换,图3
cv2.fillPoly(img, [pts], 1.0)#由于img是200*200, 所以pts超过200的自然就不会画在图上
# cv2.imshow("img", img)
# cv2.waitKey(0)
return torch.Tensor(img).unsqueeze(0)
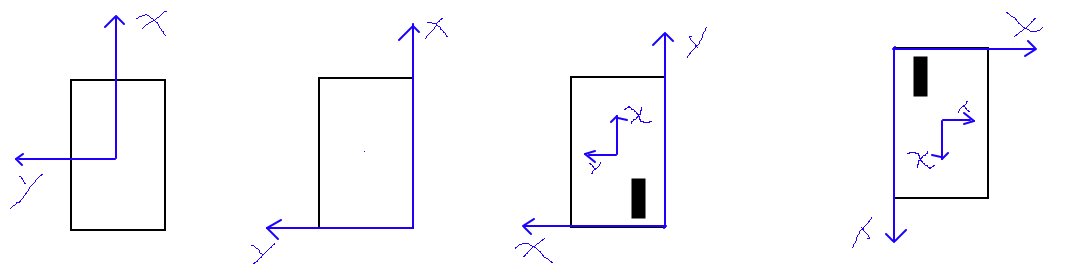
以上代码的坐标系如图变化,其实xy坐标系对换之后就是图像坐标系了,可以直接画图,只是它原点在右下角,我们把原点转到左上角就是图像坐标系。这个时候原本的自车坐标系在图像上面显示是向下的。
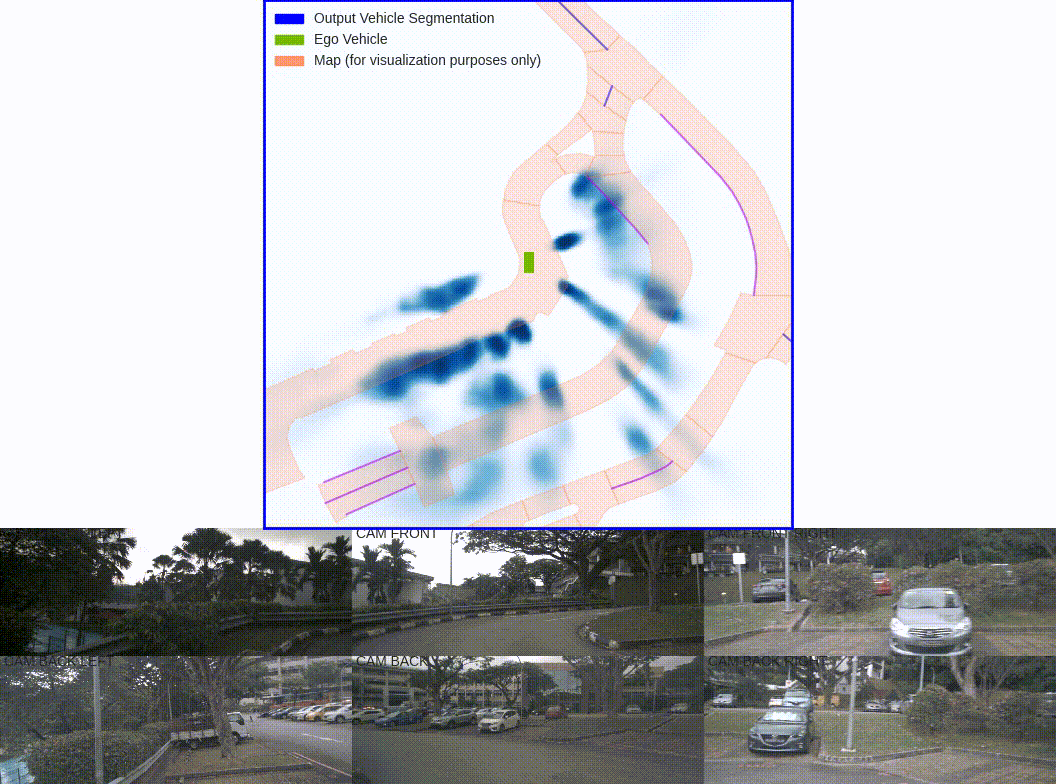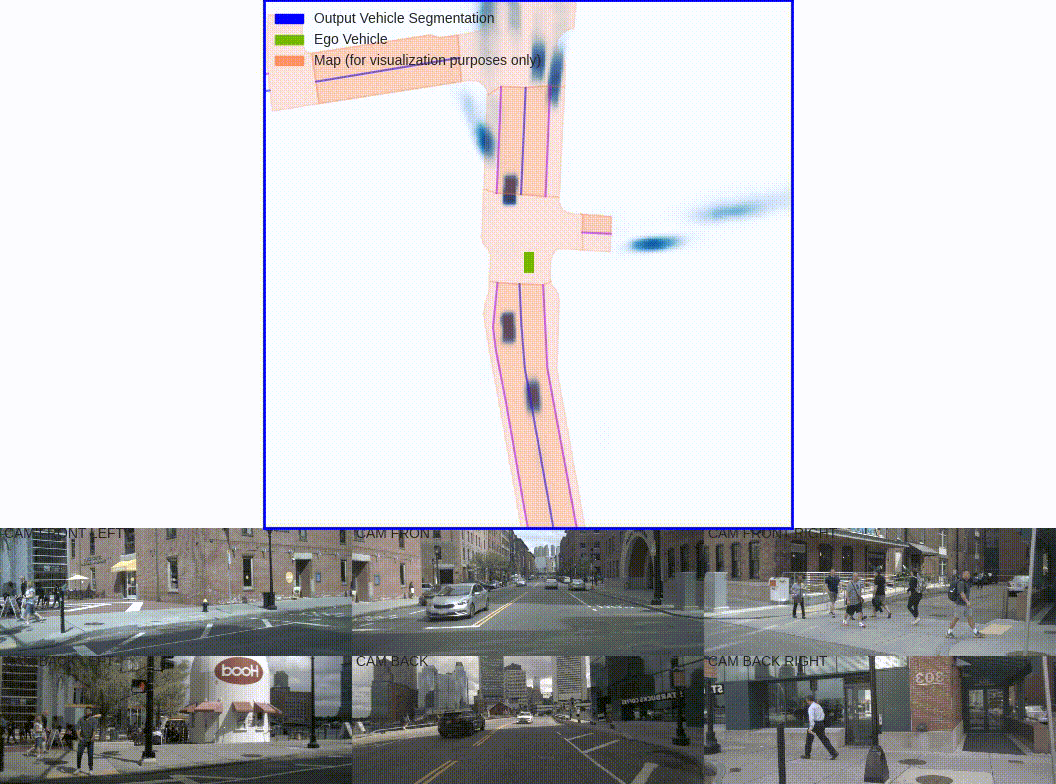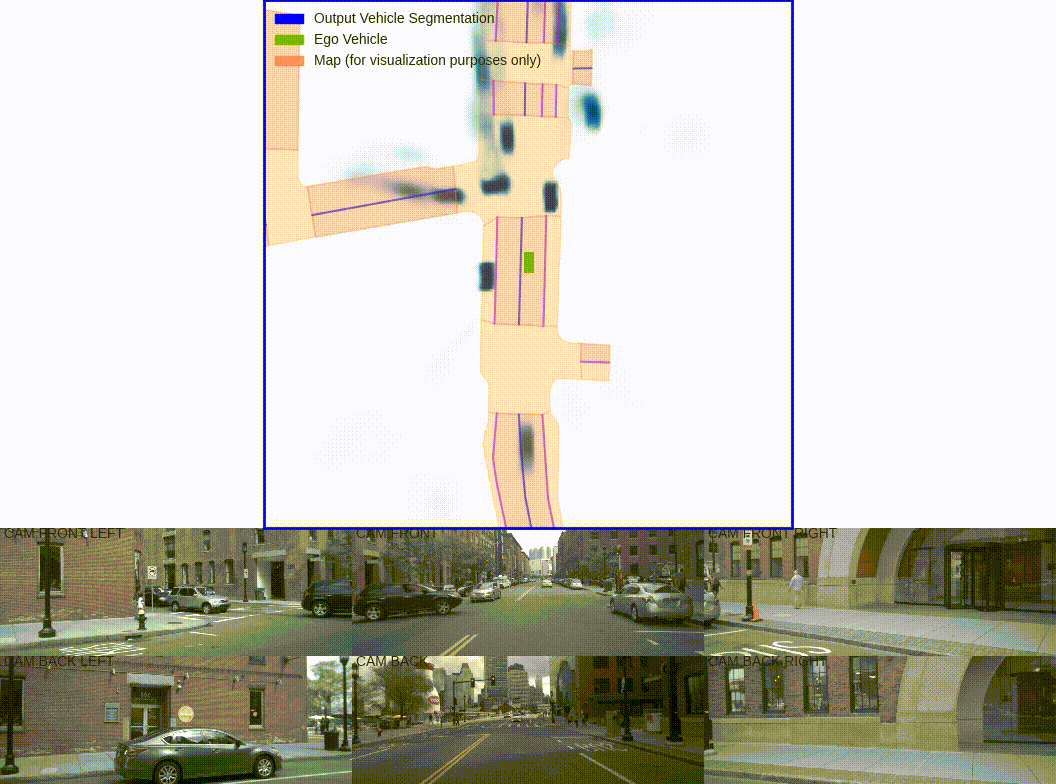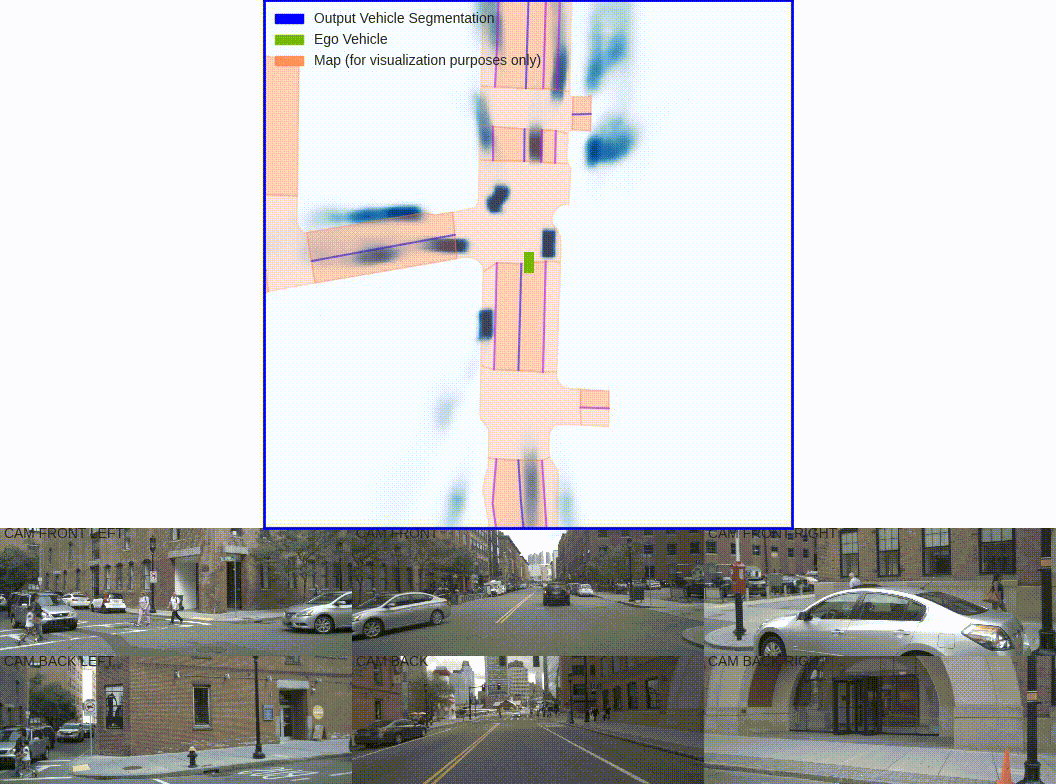
可视化训练的时候5张图构成的这里的binimg二值图像.
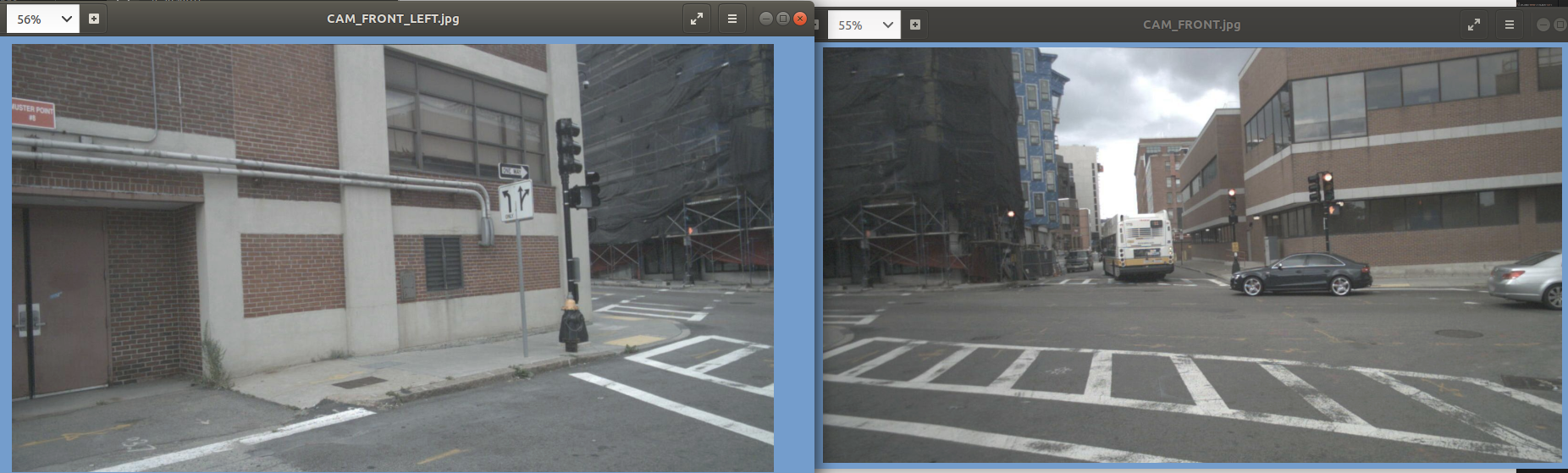


可见,这里有个问题就是图像上面不可见的目标,这里没有过滤就显示作为gt二值图了。圆点是自车位置这里是为了观察自车位置所在点,实际gt的二值图是没有的。可以看到自车往前走是向下的。
附上nuscene提供的
//l/envs/torch1.7/lib/python3.7/site-packages/nuscenes/utils/data_classes.py
class Box:
""" Simple data class representing a 3d box including, label, score and velocity. """
def __init__(self,
center: List[float],
size: List[float],
orientation: Quaternion,
label: int = np.nan,
score: float = np.nan,
velocity: Tuple = (np.nan, np.nan, np.nan),
name: str = None,
token: str = None):
"""
:param center: Center of box given as x, y, z.
:param size: Size of box in width, length, height.
:param orientation: Box orientation.
:param label: Integer label, optional.
:param score: Classification score, optional.
:param velocity: Box velocity in x, y, z direction.
:param name: Box name, optional. Can be used e.g. for denote category name.
:param token: Unique string identifier from DB.
"""
assert not np.any(np.isnan(center))
assert not np.any(np.isnan(size))
assert len(center) == 3
assert len(size) == 3
assert type(orientation) == Quaternion
self.center = np.array(center)
self.wlh = np.array(size)
self.orientation = orientation
self.label = int(label) if not np.isnan(label) else label
self.score = float(score) if not np.isnan(score) else score
self.velocity = np.array(velocity)
self.name = name
self.token = token
def __eq__(self, other):
center = np.allclose(self.center, other.center)
wlh = np.allclose(self.wlh, other.wlh)
orientation = np.allclose(self.orientation.elements, other.orientation.elements)
label = (self.label == other.label) or (np.isnan(self.label) and np.isnan(other.label))
score = (self.score == other.score) or (np.isnan(self.score) and np.isnan(other.score))
vel = (np.allclose(self.velocity, other.velocity) or
(np.all(np.isnan(self.velocity)) and np.all(np.isnan(other.velocity))))
return center and wlh and orientation and label and score and vel
def __repr__(self):
repr_str = 'label: {}, score: {:.2f}, xyz: [{:.2f}, {:.2f}, {:.2f}], wlh: [{:.2f}, {:.2f}, {:.2f}], ' \
'rot axis: [{:.2f}, {:.2f}, {:.2f}], ang(degrees): {:.2f}, ang(rad): {:.2f}, ' \
'vel: {:.2f}, {:.2f}, {:.2f}, name: {}, token: {}'
return repr_str.format(self.label, self.score, self.center[0], self.center[1], self.center[2], self.wlh[0],
self.wlh[1], self.wlh[2], self.orientation.axis[0], self.orientation.axis[1],
self.orientation.axis[2], self.orientation.degrees, self.orientation.radians,
self.velocity[0], self.velocity[1], self.velocity[2], self.name, self.token)
def translate(self, x: np.ndarray) -> None:
"""
Applies a translation.
:param x: <np.float: 3, 1>. Translation in x, y, z direction.
"""
self.center += x
def rotate(self, quaternion: Quaternion) -> None:
"""
Rotates box.
:param quaternion: Rotation to apply.
"""
self.center = np.dot(quaternion.rotation_matrix, self.center)
self.orientation = quaternion * self.orientation
self.velocity = np.dot(quaternion.rotation_matrix, self.velocity)
def corners(self, wlh_factor: float = 1.0) -> np.ndarray:
"""
Returns the bounding box corners.
:param wlh_factor: Multiply w, l, h by a factor to scale the box.
:return: <np.float: 3, 8>. First four corners are the ones facing forward.
The last four are the ones facing backwards.
"""
w, l, h = self.wlh * wlh_factor
# 3D bounding box corners. (Convention: x points forward, y to the left, z up.)
x_corners = l / 2 * np.array([1, 1, 1, 1, -1, -1, -1, -1])
y_corners = w / 2 * np.array([1, -1, -1, 1, 1, -1, -1, 1])
z_corners = h / 2 * np.array([1, 1, -1, -1, 1, 1, -1, -1])
corners = np.vstack((x_corners, y_corners, z_corners))
# Rotate
corners = np.dot(self.orientation.rotation_matrix, corners)
# Translate
x, y, z = self.center
corners[0, :] = corners[0, :] + x
corners[1, :] = corners[1, :] + y
corners[2, :] = corners[2, :] + z
return corners
def bottom_corners(self) -> np.ndarray:
"""
Returns the four bottom corners.
:return: <np.float: 3, 4>. Bottom corners. First two face forward, last two face backwards.
"""
return self.corners()[:, [2, 3, 7, 6]]
通过create_frustum函数得到采样点frustum[41,8,22,3],这里的41是有41个深度值,值域[4-45],22是图像统一resize、crop的大小为[128,352], 下采样16倍为[8, 22], 22里面每个值是s=352/16, [0, s, 2s,3s,4s,..] 即[0, 16.7143, 33.4286, 50.1429, 66.8571, 83.5714, 100.2857, ..., 351]. 在(128, 352)图上每隔16个点取值,同时每个点配41个深度值。具体如何整出[41,8,22,3],可以看如下链接:
https://www.cnblogs.com/yanghailin/p/17452610.html
def create_frustum(self):
# make grid in image plane
# 模型输入图片大小,ogfH:128, ogfW:352
ogfH, ogfW = self.data_aug_conf['final_dim']
# 输入图片下采样
16倍的大小,fH:8, fW:22
fH, fW = ogfH // self.downsample
ogfW // self.downsample
# ds取值范围为4~44,采样间隔为1
ds = torch.arange(*self.grid_conf['dbound'], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)
D, _, _ = ds.shape
# xs取值范围为0~351,在该范围内等间距取22个点,然后扩展维度,最终维度为(41,8,22)
xs = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(1, 1, fW).expand(D, fH, fW)
# ys取值范围为0~127,在该范围内等间距取8个点,然后扩展维度,最终维度为(41,8,22)
ys = torch.linspace(0, ogfH - 1, fH, dtype=torch.float).view(1, fH, 1).expand(D, fH, fW)
# D x H x W x 3
# frustum维度为(41,8,22,3)
frustum = torch.stack((xs, ys, ds), -1)
return nn.Parameter(frustum, requires_grad=False)
get_geometry函数把frustum [41, 8, 22, 3]通过坐标系转换到自车坐标系下。

# x: shape[b, 5, 3, 128, 352]
# rots: shape[b, 5, 3, 3]
# trans: shape[b, 5, 3]
# intrins: shape[b, 5, 3, 3]
# post_rots: shape[b, 5, 3, 3]
# post_trans: shape[b, 5, 3]
def get_geometry(self, rots, trans, intrins, post_rots, post_trans):
"""Determine the (x,y,z) locations (in the ego frame) of the points in the point cloud.
Returns B x N x D x H/downsample x W/downsample x 3
"""
B, N, _ = trans.shape
#self.frustum [41, 8, 22, 3] [D, H, W, 3]
# undo post-transformation
# B x N x D x H x W x 3 [41, 8, 22, 3] - [b, 5, 1, 1, 1, 3]
points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3) #points [2, 5, 41, 8, 22, 3]
#pts = points.unsqueeze(-1)#[2, 5, 41, 8, 22, 3, 1]
points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1)) #points [b, 5, 41, 8, 22, 3, 1]
#https://blog.csdn.net/ouyangandy/article/details/96840781
#https://yanghailin.blog.csdn.net/article/details/130460868?spm=1001.2014.3001.5502 看这里的最下面公式本身就乘以了个z
# cam_to_ego 归一化平面整到成像平面
#ccc = points[:, :, :, :, :, 2:3] [2, 5, 41, 8, 22, 1, 1] 4,5,6,...,43, 44, 45
#points 这里得到的是哪个坐标系下的?
points = torch.cat((points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
points[:, :, :, :, :, 2:3]
), 5) #points [2, 5, 41, 8, 22, 3, 1]
combine = rots.matmul(torch.inverse(intrins)) #combine[2, 5, 3, 3]
points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
points += trans.view(B, N, 1, 1, 1, 3) #points [b, 5, 41, 8, 22, 3]
# print(points[0][0][0][0][0])
# print(points[0][0][0][0][1])
# print(points[0][0][0][0][2])
# print(points[0][0][0][0][3])
# print(points[0][0][0][0][4])
# print(points[0][0][0][0][5])
# print(points[0][0][0][0][6])
# tensor([5.6902, 2.5839, 2.1921], device='cuda:0')
# tensor([5.6915, 2.3457, 2.1874], device='cuda:0')
# tensor([5.6928, 2.1075, 2.1827], device='cuda:0')
# tensor([5.6942, 1.8692, 2.1780], device='cuda:0')
# tensor([5.6955, 1.6310, 2.1733], device='cuda:0')
# tensor([5.6968, 1.3928, 2.1686], device='cuda:0')
# tensor([5.6981, 1.1546, 2.1639], device='cuda:0')
#[b, 5, 41, 8, 22, 3]
return points
可视化这里points,可视化代码:
def show_geom(self, geom):#[b, 5, 41, 8, 22, 3]
geom = geom.cpu().detach().numpy()
geom_one = geom[0].reshape(5, -1, 3) #[5, 7216, 3]
from matplotlib import pyplot as plt
plt.figure(figsize=(12, 8))
colors = ['r', 'g', 'b', 'c', 'm'] # 颜色列表
# x = geom_one[:, :, 0]
for i in range(5):
plt.scatter(geom_one[i, :, 0], geom_one[i, :, 1], 0.5, c=colors[i])
plt.axis('image')
plt.show()
plt.savefig("./geom2.png")
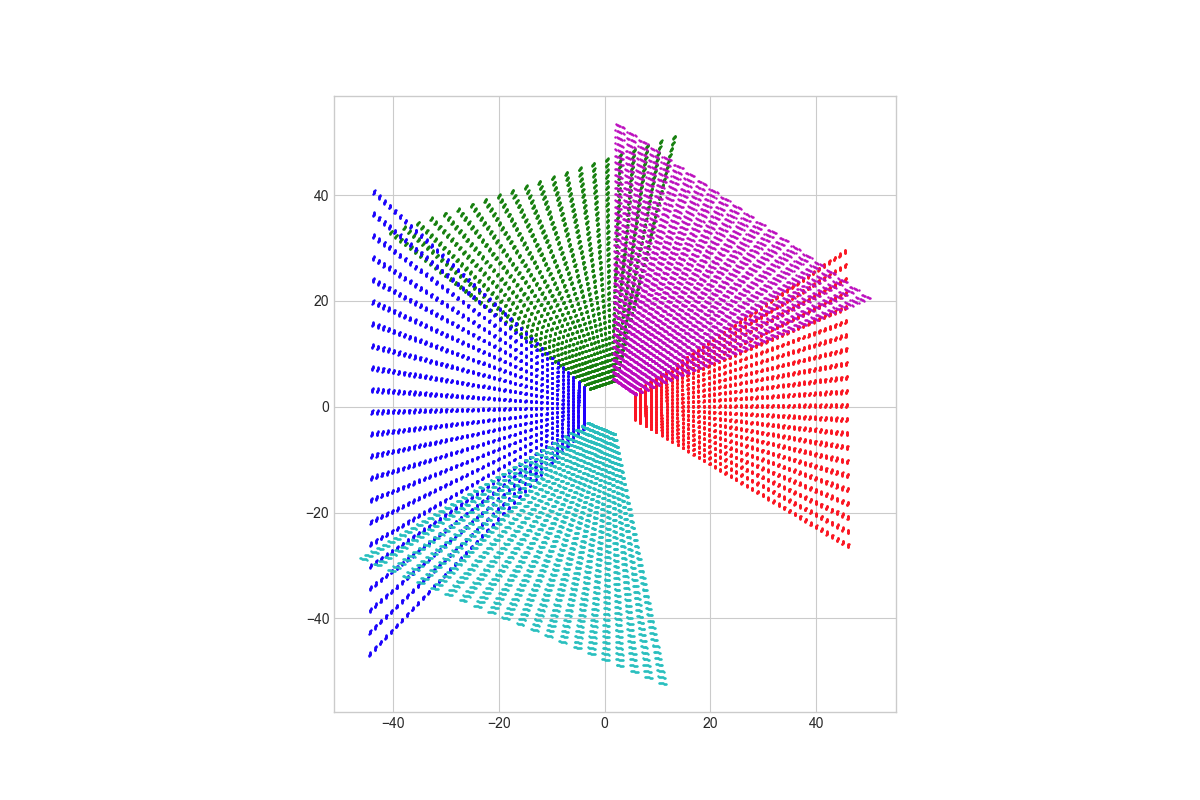
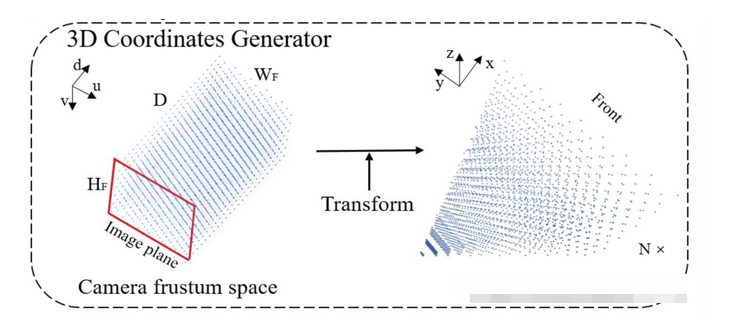
其中一个前视摄像头,

可视化固定深度的,
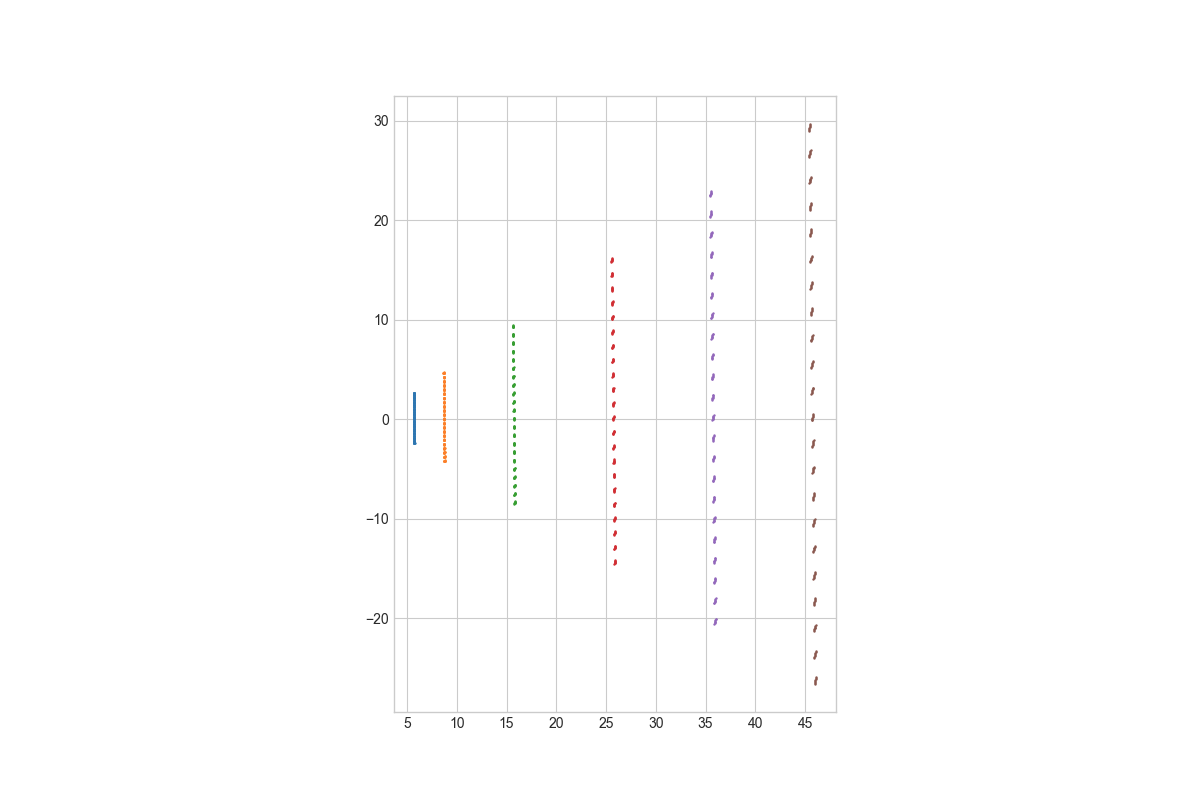
实际的是立体,类似于这样:
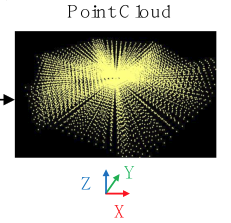
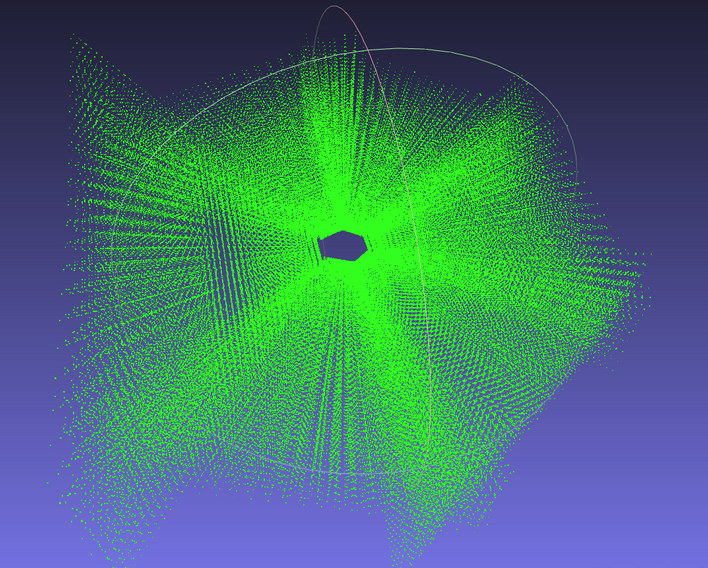
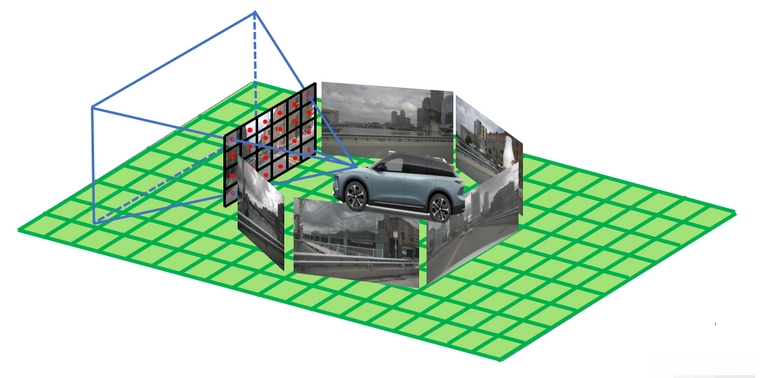
所以这里就不难理解论文中的插图,
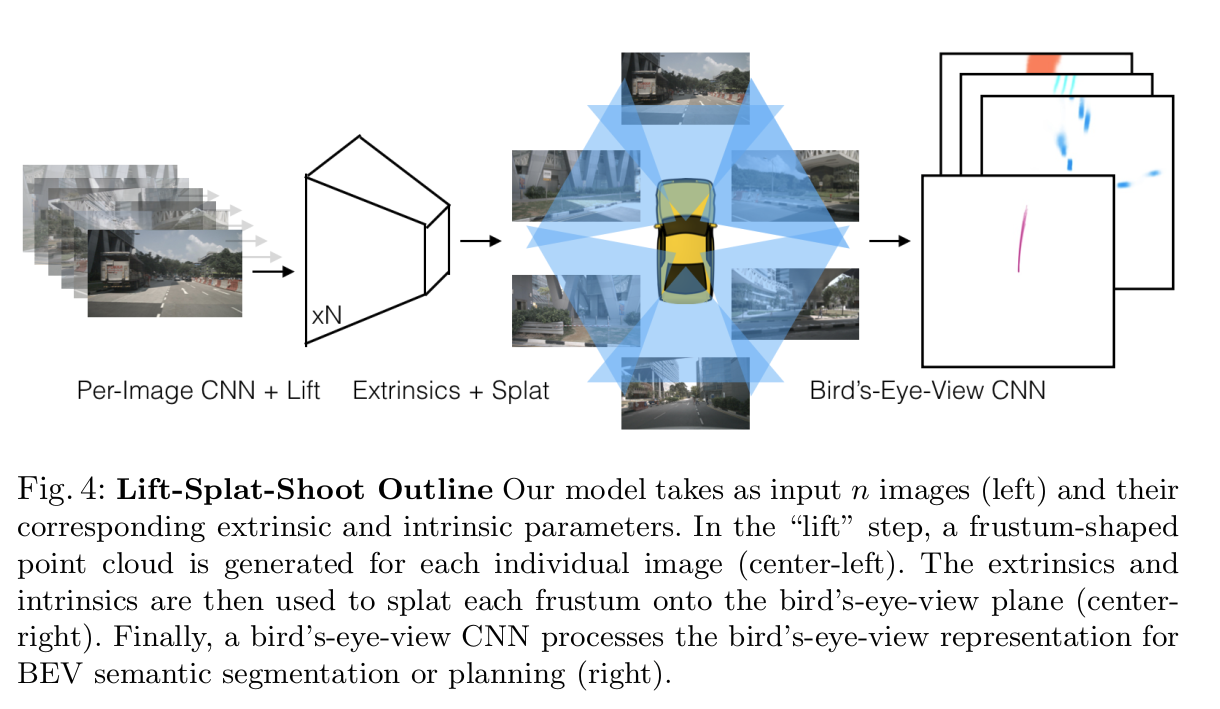
def get_cam_feats(self, x):#x: [B, N, 3, 128, 352]
"""Return B x N x D x H/downsample x W/downsample x C
"""
B, N, C, imH, imW = x.shape
x = x.view(B*N, C, imH, imW) #[10, 3, 128, 352]
x = self.camencode(x) #x [10, 64, 41, 8, 22]
x = x.view(B, N, self.camC, self.D, imH//self.downsample, imW//self.downsample) #x [b, 5, 64, 41, 8, 22]
x = x.permute(0, 1, 3, 4, 5, 2) #[b, 5, 41, 8, 22, 64]
return x
x = self.get_cam_feats(x) #out_x:[b, 5, 41, 8, 22, 64] in_x:[b, 5, 3, 128, 352]
def get_cam_feats(self, x):#x: [B, N, 3, 128, 352]
"""Return B x N x D x H/downsample x W/downsample x C
"""
B, N, C, imH, imW = x.shape
x = x.view(B*N, C, imH, imW) #[b×5, 3, 128, 352]
x = self.camencode(x) #x [b×5, 64, 41, 8, 22]
x = x.view(B, N, self.camC, self.D, imH//self.downsample, imW//self.downsample) #x [b, 5, 64, 41, 8, 22]
x = x.permute(0, 1, 3, 4, 5, 2) #[b, 5, 41, 8, 22, 64]
return x
这里的camEncode是把图片输入x[b*5, 3, 128, 352]变成[b×5, 64, 41, 8, 22], 也即论文中这个图:
在网络中用softmax操作把值归一化到0-1之间的概率,作为深度的一个概率分布。深度D=64,特征C=64,一个像素值给配上(64*41)矩阵,当这个像素比如35m的深度,那个35米处的特征就选中就是深颜色高亮。就是35米的概率值大比如0.99这样。这些都是隐式的让网络学,并没有真值约束。
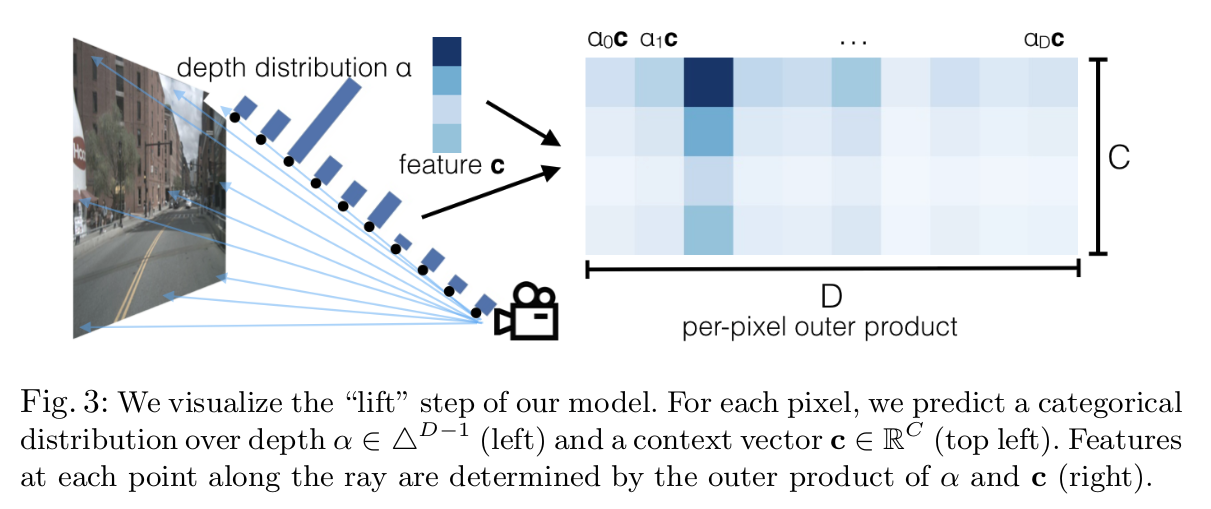
class CamEncode(nn.Module):
def __init__(self, D, C, downsample):#D41 C64
super(CamEncode, self).__init__()
self.D = D
self.C = C
self.trunk = EfficientNet.from_pretrained("efficientnet-b0")
#432
self.up1 = Up(320+112, 512)
self.depthnet = nn.Conv2d(512, self.D + self.C, kernel_size=1, padding=0)
#x [10, 41, 8, 22]
def get_depth_dist(self, x, eps=1e-20):
return x.softmax(dim=1)
def get_depth_feat(self, x):#x[10, 3, 128, 352]
x = self.get_eff_depth(x) #x[10, 512, 8, 22]
# Depth out_num=self.D + self.C = 41 + 64 = 105
x = self.depthnet(x) #x[10, 105, 8, 22]
depth = self.get_depth_dist(x[:, :self.D])#x[10, 41, 8, 22]
# aa = depth.unsqueeze(1) #[10, 1, 41, 8, 22]
# bb = x[:, self.D:(self.D + self.C)]#[10, 64, 8, 22]
# cc = x[:, self.D:(self.D + self.C)].unsqueeze(2)#[10, 64, 1, 8, 22]
new_x = depth.unsqueeze(1) * x[:, self.D:(self.D + self.C)].unsqueeze(2)#[10, 64, 41, 8, 22]
return depth, new_x
def get_eff_depth(self, x):#x[10, 3, 128, 352]
# adapted from https://github.com/lukemelas/EfficientNet-PyTorch/blob/master/efficientnet_pytorch/model.py#L231
endpoints = dict()
# Stem
x = self.trunk._swish(self.trunk._bn0(self.trunk._conv_stem(x)))
prev_x = x
# Blocks
for idx, block in enumerate(self.trunk._blocks):
drop_connect_rate = self.trunk._global_params.drop_connect_rate
if drop_connect_rate:
drop_connect_rate *= float(idx) / len(self.trunk._blocks) # scale drop connect_rate
x = block(x, drop_connect_rate=drop_connect_rate)
if prev_x.size(2) > x.size(2):
endpoints['reduction_{}'.format(len(endpoints)+1)] = prev_x
prev_x = x
# Head
endpoints['reduction_{}'.format(len(endpoints)+1)] = x
x = self.up1(endpoints['reduction_5'], endpoints['reduction_4'])
return x #[10, 512, 8, 22]
def forward(self, x): #x[10, 3, 128, 352]
depth, x = self.get_depth_feat(x) #depth [10, 41, 8, 22]
#x [10, 64, 41, 8, 22]
return x
这里voxel_pooling是一个重点函数,这里的geom_feats是点云位置坐标,x是提取的图像特征。需要根据点云坐标去图像对应位置拉取特征。
这里的点云和x坐标是一一对应的。图像特征是图像坐标系x右y下,geom_feats也是根据图像x右y下一个个点变换到ego坐标系的。就是说x的第一个点坐标和geom_feats的第一个坐标是一一对应的。
step1:geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long()
这个由自车坐标系拉到右下角,x和y上面的分辨率是0.5米一格(dx是[0.5, 0.5, 20])。这里有个细节就是,在做真值gt的时候get_binimg函数也是有个把坐标原点拉到右下角,摘自 get_binimg函数
(意思是把坐标系挪到右下角 pts = np.round( (pts - self.bx[:2] + self.dx[:2]/2.) / self.dx[:2] ).astype(np.int32)
pts[:, [1, 0]] = pts[:, [0, 1]] #坐标系xy对换,图3)
但是这里没有x,y对换,为什么呢?自己想
最后的这里对换了?(final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]])
step2:geom_feats = torch.cat((geom_feats, batch_ix), 1) #geom_feats[72160, 4]
这里把batch_id加在geom_feats后,由于上面geom_feats = geom_feats.view(Nprime, 3)把batch维度合并了,这里加上这个点是属于哪个batchsize的。
step3:
x = x[kept] # [68527, 64] <-- [72160, 64]
geom_feats = geom_feats[kept] #[68527, 4] (X, Y, Z, B)
这里通过kept过滤,只保留[200, 200,1]内的点,dx是[0.5, 0.5, 20],所以就是保留[100, 100, 20]米的特征。 检测范围就是自车前50米后50米、左50米右50米。
这里x和geom_feats都是通过kept过滤,就是说x和geom_feats是一一对应的。
step4:
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)+ geom_feats[:, 1] * (self.nx[2] * B)+ geom_feats[:, 2] * B+ geom_feats[:, 3]
#geom_feats: [2, 5, 41, 8, 22, 3]
#x: [2, 5, 41, 8, 22, 64]
def voxel_pooling(self, geom_feats, x):
B, N, D, H, W, C = x.shape
Nprime = B*N*D*H*W #72160
# flatten x
x = x.reshape(Nprime, C) #[72160, 64]
#bx = self.bx #[-49.75, -49.75, 0]
#self.dx [0.5, 0.5, 20] parameter(3, )
# t0 = self.bx - self.dx / 2. #tensor(3) [-50, -50, -10]
# flatten indices
# geom_feats [2, 5, 41, 8, 22, 3]
# for i in range(22):
# for j in range(3):
# print(geom_feats[0][0][40][6][i][j])
#- (self.bx - self.dx/2.) [50, 50, 10] self.dx[0.5, 0.5, 20]
##step1:
geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long() ##变为整数 [2, 5, 41, 8, 22, 3]
# [72160, 3]
geom_feats = geom_feats.view(Nprime, 3) #[72160, 3]
#batch_ix [72160, 1]
batch_ix = torch.cat([torch.full([Nprime//B, 1], ix,
device=x.device, dtype=torch.long) for ix in range(B)])
#step2:
geom_feats = torch.cat((geom_feats, batch_ix), 1) #geom_feats[72160, 4]
#self.nx values[200,200,1]
# filter out points that are outside box || kept[72160,]
#step3:
kept = (geom_feats[:, 0] >= 0) & (geom_feats[:, 0] < self.nx[0])\
& (geom_feats[:, 1] >= 0) & (geom_feats[:, 1] < self.nx[1])\
& (geom_feats[:, 2] >= 0) & (geom_feats[:, 2] < self.nx[2])
x = x[kept] ##[72160, 64] --> [68527, 64]
geom_feats = geom_feats[kept] #[68527, 4] (X, Y, Z, B)
# get tensors from the same voxel next to each other #ranks [68621,] self.nx value[200, 200, 1]
# geom_feats[68621, 4]
# ranks:[68621,] 把200*200平铺成一维,ranks就是geom_feats在平铺的200*200一维数组中的位置
#step4:
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)\
+ geom_feats[:, 1] * (self.nx[2] * B)\
+ geom_feats[:, 2] * B\
+ geom_feats[:, 3]
sorts = ranks.argsort() #[68621,] 由小到大的索引
#x[68621,64] geom_feats[68621,4] ranks[68621]
x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts]
#step5:
# cumsum trick out_x:[21465,64] geom_feats[21465,4]
if not self.use_quickcumsum:
x, geom_feats = cumsum_trick(x, geom_feats, ranks)
else:
x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks)
#x[20192, 64] geom_feats[20192, 4]
# griddify (B x C x Z x X x Y) || final[2, 64, 1, 200, 200]
#final[b, 64, 1, 200, 200] C=64 self.nx[200, 200, 1]
final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device)
final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x
#ccc [b, 64, 200, 200] final[b, 64, 1, 200, 200]
# ccc = final.unbind(dim=2) #tuple 1
# collapse Z #final [2, 64, 200, 200]
final = torch.cat(final.unbind(dim=2), 1)
return final
step4:
假设 geom_feats 的形状为 [20, 4],即有 20 个点,每个点有 4 个坐标 [X, Y, Z, B]。为了计算每个点的 ranks 值,我们需要知道具体的 self.nx 和批次大小 B 的值。
假设参数如下:
self.nx = [200, 200, 1],即体素网格大小。- 批次大小
B = 2。
下面列出一个假设的 geom_feats 数组(20 个样本)及其对应的 ranks 计算。
假设的 geom_feats 值
假设 geom_feats 的坐标如下:
| Index | X | Y | Z | B |
|---|---|---|---|---|
| 0 | 10 | 15 | 0 | 0 |
| 1 | 10 | 15 | 0 | 1 |
| 2 | 10 | 16 | 0 | 0 |
| 3 | 11 | 15 | 0 | 0 |
| 4 | 11 | 15 | 1 | 0 |
| 5 | 11 | 16 | 0 | 0 |
| 6 | 20 | 25 | 0 | 1 |
| 7 | 25 | 30 | 0 | 0 |
| 8 | 30 | 35 | 0 | 1 |
| 9 | 35 | 40 | 0 | 0 |
| 10 | 40 | 45 | 0 | 1 |
| 11 | 45 | 50 | 0 | 0 |
| 12 | 50 | 55 | 0 | 1 |
| 13 | 55 | 60 | 0 | 0 |
| 14 | 60 | 65 | 0 | 1 |
| 15 | 65 | 70 | 0 | 0 |
| 16 | 70 | 75 | 0 | 1 |
| 17 | 75 | 80 | 0 | 0 |
| 18 | 80 | 85 | 0 | 1 |
| 19 | 85 | 90 | 0 | 0 |
计算公式
根据公式:
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B) \
+ geom_feats[:, 1] * (self.nx[2] * B) \
+ geom_feats[:, 2] * B \
+ geom_feats[:, 3]
计算前:
self.nx[1] * self.nx[2] * B = 200 * 1 * 2 = 400self.nx[2] * B = 1 * 2 = 2
逐个计算 ranks
| Index | X | Y | Z | B | Ranks Calculation | Ranks |
|---|---|---|---|---|---|---|
| 0 | 10 | 15 | 0 | 0 | (10 × 400 + 15 × 2 + 0 × 2 + 0 = 4030) | 4030 |
| 1 | 10 | 15 | 0 | 1 | (10 × 400 + 15 × 2 + 0 × 2 + 1 = 4031) | 4031 |
| 2 | 10 | 16 | 0 | 0 | (10 × 400 + 16 × 2 + 0 × 2 + 0 = 4032) | 4032 |
| 3 | 11 | 15 | 0 | 0 | (11 × 400 + 15 × 2 + 0 × 2 + 0 = 4430) | 4430 |
| 4 | 11 | 15 | 1 | 0 | (11 × 400 + 15 × 2 + 1 × 2 + 0 = 4432) | 4432 |
| 5 | 11 | 16 | 0 | 0 | (11 × 400 + 16 × 2 + 0 × 2 + 0 = 4432) | 4432 |
| 6 | 20 | 25 | 0 | 1 | (20 × 400 + 25 × 2 + 0 × 2 + 1 = 8031) | 8031 |
| 7 | 25 | 30 | 0 | 0 | (25 × 400 + 30 × 2 + 0 × 2 + 0 = 10060) | 10060 |
| 8 | 30 | 35 | 0 | 1 | (30 × 400 + 35 × 2 + 0 × 2 + 1 = 12071) | 12071 |
| 9 | 35 | 40 | 0 | 0 | (35 × 400 + 40 × 2 + 0 × 2 + 0 = 14080) | 14080 |
| 10 | 40 | 45 | 0 | 1 | (40 × 400 + 45 × 2 + 0 × 2 + 1 = 16091) | 16091 |
| 11 | 45 | 50 | 0 | 0 | (45 × 400 + 50 × 2 + 0 × 2 + 0 = 18100) | 18100 |
| 12 | 50 | 55 | 0 | 1 | (50 × 400 + 55 × 2 + 0 × 2 + 1 = 20111) | 20111 |
| 13 | 55 | 60 | 0 | 0 | (55 × 400 + 60 × 2 + 0 × 2 + 0 = 22120) | 22120 |
| 14 | 60 | 65 | 0 | 1 | (60 × 400 + 65 × 2 + 0 × 2 + 1 = 24131) | 24131 |
| 15 | 65 | 70 | 0 | 0 | (65 × 400 + 70 × 2 + 0 × 2 + 0 = 26140) | 26140 |
| 16 | 70 | 75 | 0 | 1 | (70 × 400 + 75 × 2 + 0 × 2 + 1 = 28151) | 28151 |
| 17 | 75 | 80 | 0 | 0 | (75 × 400 + 80 × 2 + 0 × 2 + 0 = 30160) | 30160 |
| 18 | 80 | 85 | 0 | 1 | (80 × 400 + 85 × 2 + 0 × 2 + 1 = 32171) | 32171 |
| 19 | 85 | 90 | 0 | 0 | (85 × 400 + 90 × 2 + 0 × 2 + 0 = 34180) | 34180 |
这些计算结果生成了每个点的 ranks 值,用于表示该点在展平的索引中的位置。
这里需要注意计算公式,
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B) + geom_feats[:, 1] * (self.nx[2] * B) + geom_feats[:, 2] * B + geom_feats[:, 3]
ranks = geom_feats[:, 0] ×400+ geom_feats[:, 1] *2+ geom_feats[:, 2] *2 +geom_feats[:, 3]
上面的index不同的xyz值可以产生相同的ranks值,但是不同的B是不会产生相同的值。
- 组合 1:
(X=1, Y=100, Z=0)ranks = 1 * 200 + 100 * 1 + 0 = 200 + 100 = 300
- 组合 2:
(X=0, Y=300, Z=0)ranks = 0 * 200 + 300 * 1 + 0 = 0 + 300 = 300
这两个组合的 (X, Y, Z) 不同,但 ranks 的结果都是 300。
step4:根据ranks值由小到大排序。这里由小到大也相当于从右下角开始的原点选择。
sorts = ranks.argsort() #[68621,] 由小到大的索引
#x[68621,64] geom_feats[68621,4] ranks[68621]
x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts]
step5:x, geom_feats = cumsum_trick(x, geom_feats, ranks)
class QuickCumsum(torch.autograd.Function): #x:[68527, 64] geom_feats[68527, 4] ranks[68527]
@staticmethod
def forward(ctx, x, geom_feats, ranks):
x = x.cumsum(0) #x:[68527, 64] 累计和
kept = torch.ones(x.shape[0], device=x.device, dtype=torch.bool) #[68527,]
kept[:-1] = (ranks[1:] != ranks[:-1])
# 当前值和下面不一样的是1, 一样的是0, 拿1, 就是拿最下面大的那个
#x[19586, 64] geom_feats[19586, 4]
x, geom_feats = x[kept], geom_feats[kept]
# a = x[:1] #[1, 64]
# b = x[1:] #[19585, 64]
# c = x[:-1] #[19585, 64]
#x#[19586, 64]
x = torch.cat((x[:1], x[1:] - x[:-1]))
# save kept for backward
ctx.save_for_backward(kept)
# no gradient for geom_feats
ctx.mark_non_differentiable(geom_feats)
return x, geom_feats
用简单的数值带入函数方便理解:
import torch
x0 = torch.rand((10, 3))
x0 = torch.arange(1, 11).unsqueeze(1)
x0 = x0.expand(-1, 3)
geom_feats = torch.rand((10, 4))
ranks = torch.tensor([4,4, 202, 9,9,9,1,1,10,29])
x1 = x0.cumsum(0)
kept = torch.ones(x1.shape[0], device=x1.device, dtype=torch.bool) #最后一个为1,代表无论如何都需要求和
kept[:-1] = (ranks[1:] != ranks[:-1]) #保留不一样的地方
# 4,4,202,9,9,9,1,1,10,29
ranks[1:] : 4,202, 9, 9,9,1,1,10,29
ranks[:-1]: 4, 4, 202, 9,9,9,1, 1,10
kept[:-1] : 0, 1, 1, 0,0,1,0,1,1
#所以kept:0, 1, 1, 0,0,1,0,1,1, 1
#这里0代表就是相同的,需要累加的
#1就是累加,若1前面有0就是累加, 否则就是当前值。
x2, geom_feats = x1[kept], geom_feats[kept]
x3 = torch.cat((x2[:1], x2[1:] - x2[:-1]))
print("--x0"*8)
print(x0)
print("--x1"*8)
print(x1)
print("--x2"*8)
print(x2)
print("--x3"*8)
print(x3)
--x0--x0--x0--x0--x0--x0--x0--x0
tensor([[ 1, 1, 1], #4
[ 2, 2, 2], #4
[ 3, 3, 3], #202
[ 4, 4, 4], #9
[ 5, 5, 5], #9
[ 6, 6, 6], #9
[ 7, 7, 7], #1
[ 8, 8, 8], #1
[ 9, 9, 9], #10
[10, 10, 10]]) #29
--x1--x1--x1--x1--x1--x1--x1--x1
tensor([[ 1, 1, 1],
[ 3, 3, 3],
[ 6, 6, 6],
[10, 10, 10],
[15, 15, 15],
[21, 21, 21],
[28, 28, 28],
[36, 36, 36],
[45, 45, 45],
[55, 55, 55]])
--x2--x2--x2--x2--x2--x2--x2--x2
tensor([[ 3, 3, 3],
[ 6, 6, 6],
[21, 21, 21],
[36, 36, 36],
[45, 45, 45],
[55, 55, 55]])
--x3--x3--x3--x3--x3--x3--x3--x3
tensor([[ 3, 3, 3],
[ 3, 3, 3],
[15, 15, 15],
[15, 15, 15],
[ 9, 9, 9],
[10, 10, 10]])
以上,先看现象,ranks值:[4,4, 202, 9,9,9,1,1,10,29], 前面两个ranks值相等,所以输出累加和是[3,3,3], ranks值202不相等,那么就它自己,输出[3,3,3],再接着3个ranks9相等,对应的是[4,4,4] ,[5,5,5],[6,6,6],所以输出累计和是[15,15,15],再接着是两个1,1ranks值,对应[7,7,7]和[8,8,8],所以输出累计和是[15,15,15]。以此类推。
/media/algo/data_1/project_others/0000paper/lss/project/my/img/image-20241112095326758.png
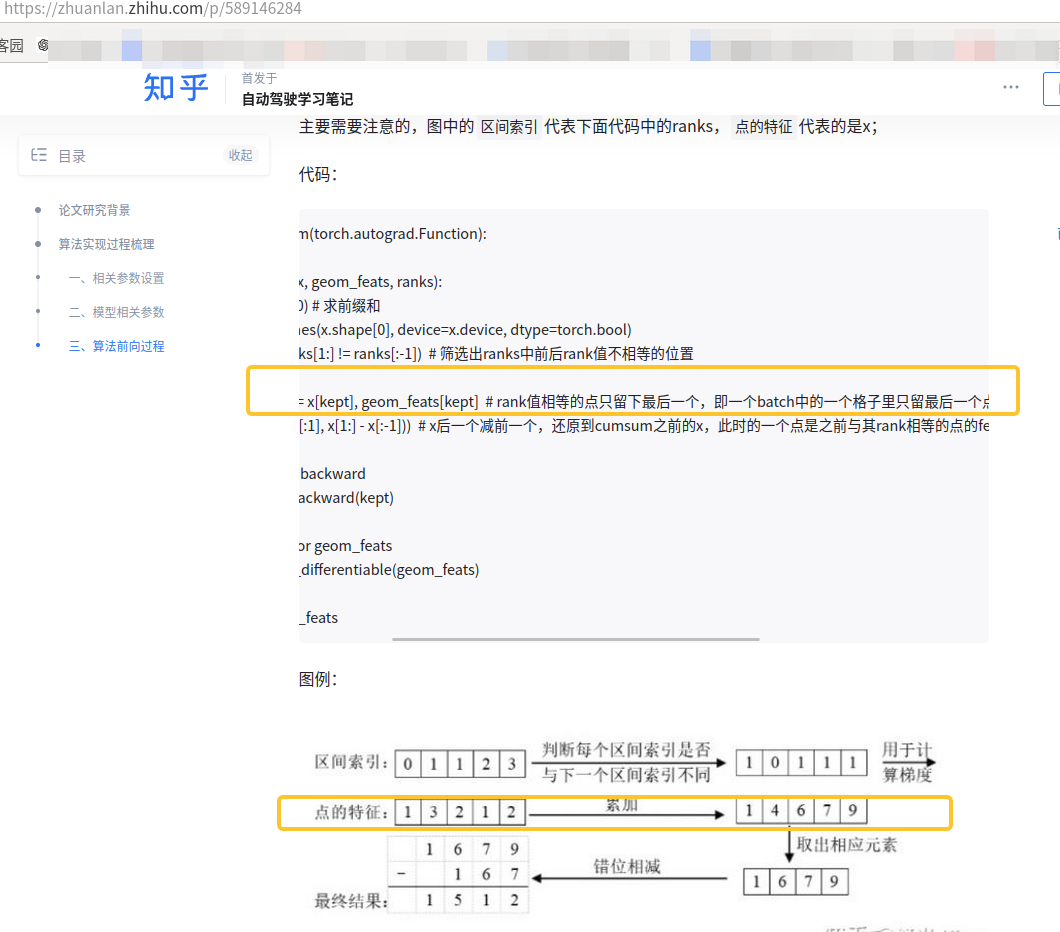
总结一下具体方法就是先累计求和,然后得到ranks不一样的地方的累计和。 然后再用下一个减去前一个得到:相同的地方就说保存累计和、不一样的地方保存本身。
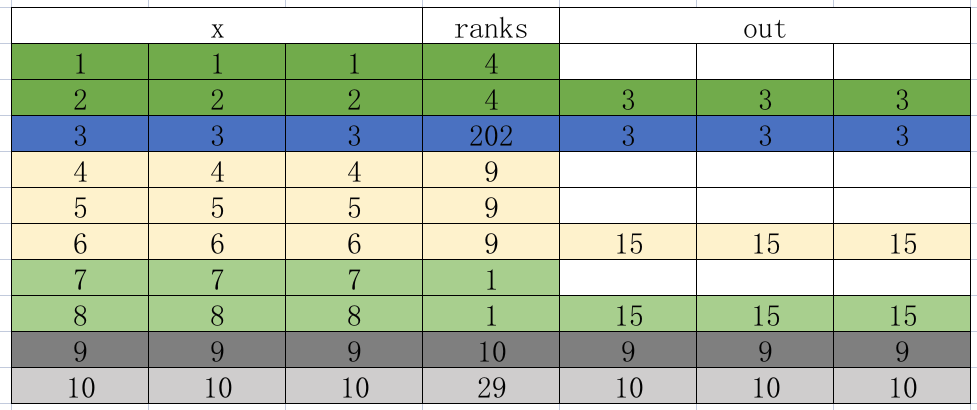
这里需要看下具体实现方法:这里的 x = x.cumsum(0) #x:[68527, 64] 累计和,
是累计和,dim=0,是一个点的特征(64维)和下一个点特征(64维)每维度求和。并不是每个点特征的累计和。网上好多博客讲解这里最后就说只保留最后一个点特征,其实是错误的。
if not self.use_quickcumsum:
x, geom_feats = cumsum_trick(x, geom_feats, ranks)
else:
x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks)
#x[20192, 64] geom_feats[20192, 4]
# griddify (B x C x Z x X x Y) || final[2, 64, 1, 200, 200]
#final[b, 64, 1, 200, 200] C=64 self.nx[200, 200, 1]
final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device)
final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x
#ccc [b, 64, 200, 200] final[b, 64, 1, 200, 200]
# ccc = final.unbind(dim=2) #tuple 1
# collapse Z #final [2, 64, 200, 200]
final = torch.cat(final.unbind(dim=2), 1)
return final




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· Trae初体验