opencv 曲线拟合

最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
算法+OpenCV】基于opencv的直线和曲线拟合与绘制（最小二乘法） https://www.cnblogs.com/fengliu-/p/8031406.html

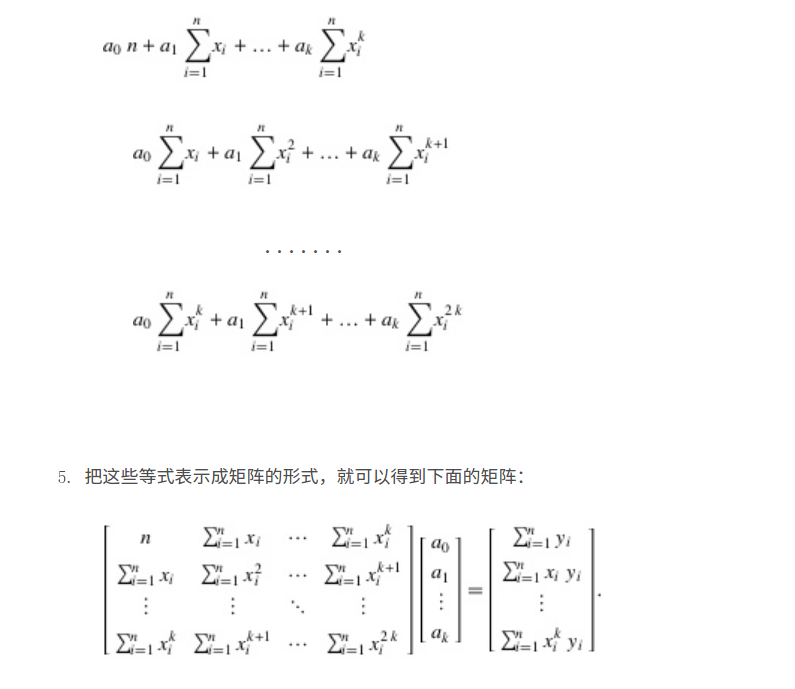
基于opencv c++代码如下：

#include <iostream>
#include <opencv.hpp>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
    //最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
    //https://www.cnblogs.com/fengliu-/p/8031406.html
    int N = points.size();
    cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
    for (int i = 0; i < n + 1; i++){
        for (int j = 0; j < n + 1; j++){
            for (int k = 0; k < N; k++){
                X.at<double>(i, j) = X.at<double>(i, j) +
                        std::pow(points[k].x, i + j);
            }
        }
    }
    cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
    for (int i = 0; i < n + 1; i++){
        for (int k = 0; k < N; k++){
            Y.at<double>(i, 0) = Y.at<double>(i, 0) +
                    std::pow(points[k].x, i) * points[k].y;
        }
    }
    A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
    cv::solve(X, Y, A, cv::DECOMP_LU);
}


int main(int argc, char **argv)
{
    string path = "/data_1/everyday/1224/2.jpeg";
    Mat img = imread(path);
    Mat img_gray,img_bi;
    cvtColor(img,img_gray,CV_BGR2GRAY);
    threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);

    vector<vector<Point> > contours;
    vector<Vec4i> hierarchy;
    findContours( img_bi, contours, hierarchy,  CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
    std::cout<<contours[0].size()<<std::endl;

    cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
    drawContours(img_draw,contours,-1,Scalar(255,255,255));


    int n = 3;
    cv::Mat A;
    FitPolynomialCurve(contours[0], n, A);
    std::vector<cv::Point> points_fitted;
    for (int x = 0; x < 800; x++)
    {
        double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
                A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3);
        points_fitted.push_back(cv::Point(x, y));
    }

    cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);

    imshow("img_src",img);
    imshow("img_draw",img_draw);
    imshow("img_bi",img_bi);
    waitKey(0);


    return 0;
}

效果图如下：

但是我后面又整了个S形状的图像，找不到能够很好拟合的函数阶数。

#include <iostream>
#include <opencv.hpp>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
    //最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
    //https://www.cnblogs.com/fengliu-/p/8031406.html
    int N = points.size();
    cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
    for (int i = 0; i < n + 1; i++){
        for (int j = 0; j < n + 1; j++){
            for (int k = 0; k < N; k++){
                X.at<double>(i, j) = X.at<double>(i, j) +
                        std::pow(points[k].x, i + j);
            }
        }
    }
    cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
    for (int i = 0; i < n + 1; i++){
        for (int k = 0; k < N; k++){
            Y.at<double>(i, 0) = Y.at<double>(i, 0) +
                    std::pow(points[k].x, i) * points[k].y;
        }
    }
    A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
    cv::solve(X, Y, A, cv::DECOMP_LU);
}

int main(int argc, char **argv)
{
    string path = "/data_1/everyday/1224/3.jpeg";
    Mat img = imread(path);
    Mat img_gray,img_bi;
    cvtColor(img,img_gray,CV_BGR2GRAY);
    threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);

    vector<vector<Point> > contours;
    vector<Vec4i> hierarchy;
    findContours( img_bi, contours, hierarchy,  CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
    std::cout<<contours[0].size()<<std::endl;

    cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
    drawContours(img_draw,contours,-1,Scalar(255,255,255));


    int n = 9;
    cv::Mat A;
    FitPolynomialCurve(contours[0], n, A);
    std::vector<cv::Point> points_fitted;
    for (int x = 0; x < 800; x++)
    {
        double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
                A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3) + A.at<double>(4, 0)*std::pow(x, 4) + A.at<double>(5, 0)*std::pow(x, 5)
                + A.at<double>(6, 0)*std::pow(x, 6) + A.at<double>(7, 0)*std::pow(x, 7) + A.at<double>(8, 0)*std::pow(x, 8) + A.at<double>(9, 0)*std::pow(x, 9);
                //+ A.at<double>(10, 0)*std::pow(x, 10) + A.at<double>(11, 0)*std::pow(x, 11) + A.at<double>(12, 0)*std::pow(x, 12);
        points_fitted.push_back(cv::Point(x, y));
    }

    cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);


    imshow("img_src",img);
    imshow("img_draw",img_draw);
    imshow("img_bi",img_bi);
    waitKey(0);


    return 0;
}

突然想明白，这个S形状曲线一个x对应好几个y，不行。需要一个x唯一对应一个y的曲线才能拟合。然后又顺手画了一个，果真可以拟合。

当然代码每次根据不同的阶数写好多A.at(6, 0)*std::pow(x, 6)，可以用如下函数自动根据x得到y：

double CurveY(double x, cv::Mat& A){
    double y = 0.0;
    double *a = A.ptr<double>();
    for (int i = 0; i < A.rows; i++){
        y += a[i] * pow(x, i);
    }
    return y;
}