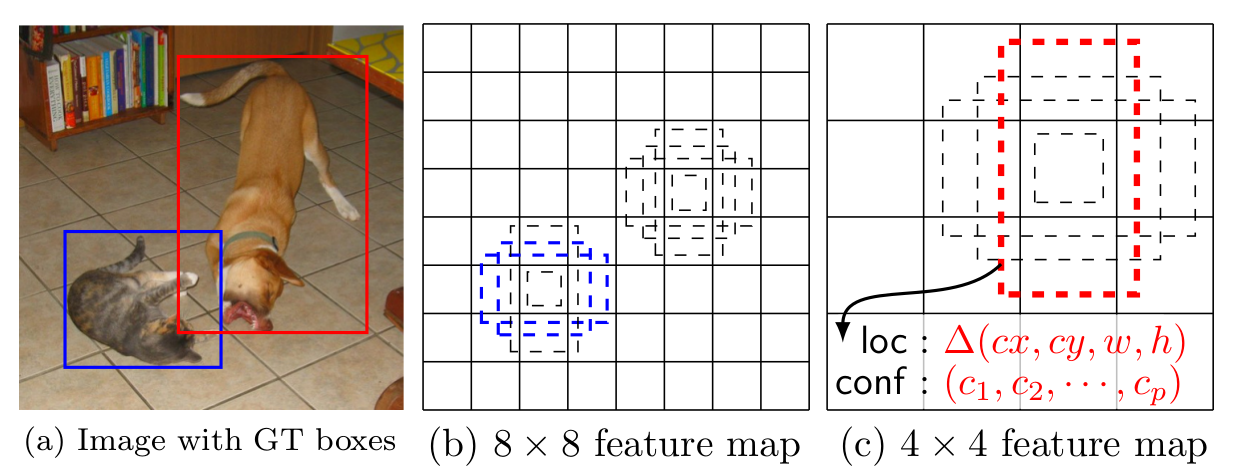
ssd 的anchor生成详解

最近面试，被各种问，特别被问到一些很细节的东西我一知半解，特尴尬。遂下定决心看懂并记住每一个细节！不怕被问！
ssd的anchor是如何生成的？
首先需要了解一些参数数值的意义：

# SSD300 CONFIGS
voc = {
    'num_classes': 21,
    'lr_steps': (80000, 100000, 120000),
    'max_iter': 1200000,
    'feature_maps': [38, 19, 10, 5, 3, 1],
    'min_dim': 300,
    'steps': [8, 16, 32, 64, 100, 300],
    'min_sizes': [30, 60, 111, 162, 213, 264],
    'max_sizes': [60, 111, 162, 213, 264, 315],
    'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]],
    'variance': [0.1, 0.2],
    'clip': True,
    'name': 'VOC',
}

这里的min_sizes和max_sizes是根据公式生成的：

直接上anchor的生成代码：prior_box.py

from __future__ import division
from math import sqrt as sqrt
from itertools import product as product
import torch

# SSD300 CONFIGS
# voc = {
#     'num_classes': 21,
#     'lr_steps': (80000, 100000, 120000),
#     'max_iter': 1200000,
#     'feature_maps': [38, 19, 10, 5, 3, 1],
#     'min_dim': 300,
#     'steps': [8, 16, 32, 64, 100, 300],
#     'min_sizes': [30, 60, 111, 162, 213, 264],
#     'max_sizes': [60, 111, 162, 213, 264, 315],
#     'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]],
#     'variance': [0.1, 0.2],
#     'clip': True,
#     'name': 'VOC',
# }


class PriorBox(object):
    """Compute priorbox coordinates in center-offset form for each source
    feature map.
    """
    def __init__(self, cfg):
        super(PriorBox, self).__init__()
        self.image_size = cfg['min_dim']
        # number of priors for feature map location (either 4 or 6)
        self.num_priors = len(cfg['aspect_ratios'])
        self.variance = cfg['variance'] or [0.1]
        self.feature_maps = cfg['feature_maps']
        self.min_sizes = cfg['min_sizes']
        self.max_sizes = cfg['max_sizes']
        self.steps = cfg['steps']
        self.aspect_ratios = cfg['aspect_ratios']
        self.clip = cfg['clip']
        self.version = cfg['name']
        for v in self.variance:
            if v <= 0:
                raise ValueError('Variances must be greater than 0')

    def forward(self):
        mean = []
        for k, f in enumerate(self.feature_maps): #[38, 19, 10, 5, 3, 1],
            for i, j in product(range(f), repeat=2):
                f_k = self.image_size / self.steps[k]
                # unit center x,y
                cx = (j + 0.5) / f_k
                cy = (i + 0.5) / f_k

                # aspect_ratio: 1
                # rel size: min_size
                s_k = self.min_sizes[k]/self.image_size
                mean += [cx, cy, s_k, s_k]

                # aspect_ratio: 1
                # rel size: sqrt(s_k * s_(k+1))
                s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size))
                mean += [cx, cy, s_k_prime, s_k_prime]

                # rest of aspect ratios
                for ar in self.aspect_ratios[k]:
                    mean += [cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]
                    mean += [cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]
        # back to torch land
        output = torch.Tensor(mean).view(-1, 4) ##[8732,4]
        if self.clip:
            output.clamp_(max=1, min=0)
        return output

这里注意init里面初始化的一些参数就是上面voc里面的。这里主要是用到了
'feature_maps': [38, 19, 10, 5, 3, 1], 是6个feature map的大小
'steps': [8, 16, 32, 64, 100, 300], 是下采样的倍数
'min_sizes': [30, 60, 111, 162, 213, 264], 相对于300大小
'max_sizes': [60, 111, 162, 213, 264, 315],相对于300大小
'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]],
'clip': True,
然后我们来解析anchor是如何生成的。
上面用product生成笛卡尔坐标，遍历每个像素位置，也就是说为每个像素位置配上anchor。
关于product，https://www.cnblogs.com/yanghailin/p/14769384.html，可以看这里3.itertools.product
或者这里简单介绍一下：
product(A,B)函数,返回A和B中的元素组成的笛卡尔积的元组，
itertools.product(*iterables, repeat=1)
iterables是可迭代对象,repeat指定iterable重复几次,即:
product(A,repeat=3)等价于product(A,A,A)

import itertools
for item in itertools.product([1,2,3,4],[100,200]):
    print(item)
    '''
(1, 100)
(1, 200)
(2, 100)
(2, 200)
(3, 100)
(3, 200)
(4, 100)
(4, 200)
    '''

 for k, f in enumerate(self.feature_maps): #[38, 19, 10, 5, 3, 1],
            for i, j in product(range(f), repeat=2):

cx，cy是feature map上面的每个点，然后再配上w和h。
注意anchor的四个值都是相对值，都是0-1的小数。

mean一般而言是4个，但是aspect_ratios个数是2的话，就是6个。
这里for循环多一轮，就会多出2个，所以是6个

for ar in self.aspect_ratios[k]:
  mean += [cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]
  mean += [cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]

s_k = self.min_sizes[k]/self.image_size
s_k_prime = sqrt(s_k * (self.max_sizes[k]/self.image_size))

[cx, cy, s_k, s_k]
[cx, cy, s_k_prime, s_k_prime]
[cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]  ##ar取2或者3
[cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]

从上面计算规则来看，前面两个是正方形，一个大的一个小的正方形。
然后后面两个是矩形，一个长的矩形，一个宽的矩形。
当k=0，f=38的时候，featuremap的大小是38，ar只有一个2，所以是一个点对应4个anchor。画图如下：

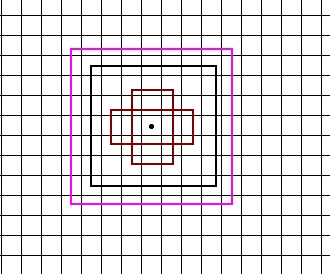
然后feature map 等于38，19, 10, 5, 3, 1也是类似的，只不过
'aspect_ratios': [[2], [2, 3], [2, 3], [2, 3], [2], [2]],
19, 10, 5的时候aspect_ratios个数为2，一个点就会对应6个anchor。
所以，整个6个大循环下来，得到的anchor的总的个数为：

还有一点就是
'min_sizes': [30, 60, 111, 162, 213, 264], 相对于300大小
'max_sizes': [60, 111, 162, 213, 264, 315],相对于300大小
相对于300大小，因为看到代码里面
s_k = self.min_sizes[k]/self.image_size
都是除以的self.image_size（300）。
然后'feature_maps': [38, 19, 10, 5, 3, 1], 是6个feature map的大小
其实这里就可以看出，在feature等于38的尺寸上面，是最大的尺寸，找的最小的min_sizes是30（相对于300），所以可以看到是在浅层特征上面找小目标！

然后anchor的格式就是下面这些值。

tensor([[0.0133, 0.0133, 0.1000, 0.1000],
        [0.0133, 0.0133, 0.1414, 0.1414],
        [0.0133, 0.0133, 0.1414, 0.0707],
        ...,
        [0.5000, 0.5000, 0.9612, 0.9612],
        [0.5000, 0.5000, 1.2445, 0.6223],
        [0.5000, 0.5000, 0.6223, 1.2445]])

最后，这里详细讲解了anchor的生成方式，其实，真的，all in code。
这里再详细不过了，要是下次再被问到，不要答不上来哦～
主要就是这4个，记住就好：

[cx, cy, s_k, s_k]
[cx, cy, s_k_prime, s_k_prime]
[cx, cy, s_k*sqrt(ar), s_k/sqrt(ar)]  ##ar取2或者3
[cx, cy, s_k/sqrt(ar), s_k*sqrt(ar)]

～～～～～2021年06月11日09:42:46 更新～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～
这里有一个很重要的细节！我是看到后面计算loss的时候才回过头来看的。因为后面看到truths直接与这里生成的anchor做相交运算。

overlaps = jaccard(
        truths,
        point_form(priors)
    )

我就在想怎么能直接做交并比呢，因为truths相对于300300的比例，难道这里的anchor也是相对于300300的吗？
然后仔细看这里的代码，发现一个细节！
就是

 for k, f in enumerate(self.feature_maps): #[38, 19, 10, 5, 3, 1],
            for i, j in product(range(f), repeat=2):
                f_k = self.image_size / self.steps[k]
                # unit center x,y
                cx = (j + 0.5) / f_k
                cy = (i + 0.5) / f_k

                # aspect_ratio: 1
                # rel size: min_size
                s_k = self.min_sizes[k]/self.image_size
                mean += [cx, cy, s_k, s_k]

第一循环是step=8， f_k = self.image_size / self.steps[k]-->f_k = 300/8=37.5
所以可以看到cx = (j + 0.5) / f_k 和 cy = (i + 0.5) / f_k都是相对于第一层feature map大小38的。
但是看到w和h都是相对于self.image_size（300）的！ s_k = self.min_sizes[k]/self.image_size。
然后整出的anchor mean += [cx, cy, s_k, s_k]可以直接和在300上面的比例直接做交并比运算。想想确实是可以的！
因为你300下采样8倍的feature map38上面，38每移动一个点在300上面相当于移动了8个点。所以，位置是相对的，映射到300上面就是乘以倍数移动。举例

j=3时候
cx=(j+0.5)/37.5=0.09333       0.09333*300=27.999
j=4时候
cx=(j+0.5)/37.5=0.12       0.12*300=36

可见，36-28=8，j变化了1，在300上面就变化了8，就是300在下采样8倍38的大小上，每移动1位就相当于在300上移动了8。
所以后面把在38大小上面的比例用在300上面，就是默认这种行为（每移动1位就相当于在300上移动了8）。但是他对应的宽和高还是按照300的比例来的。这里没有毛病。
只是位置有个倍移，宽和高还是按照300上面的比例来。
所以这里得到的anchor可以直接和groundtruth做交并比。

额外链接：
深入理解anchor https://blog.csdn.net/qianqing13579/article/details/82106664