c++ 牛顿迭代法求解多元多次方程组

参考链接如下：
原理：https://max.book118.com/html/2019/0313/8102130101002012.shtm
代码：https://wenku.baidu.com/view/b3f91c3467ec102de2bd89a3.html
例如原理链接里面的一题：

跑代码如下：

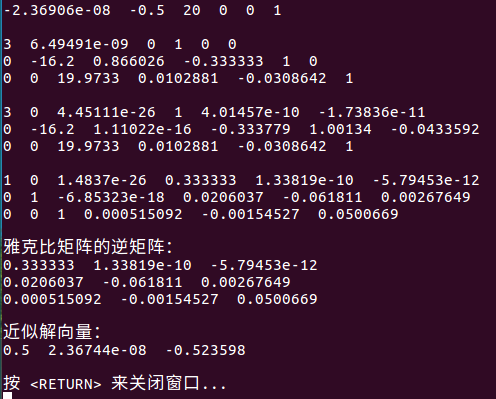
代码如下：

//经典牛顿迭代法C++实现
#include<iostream>
#include<cmath>
#define N 3               // 非线性方程组中方程个数、未知量个数
#define Epsilon 0.000000001    // 差向量1范数的上限
#define Max     1000000000000       //最大迭代次数
using namespace std;
const int N2=2*N;

int main()
{
    void ff(double xx[N],double yy[N]); //计算向量函数的因变量向量yy[N]
    void ffjacobian(double xx[N],double yy[N][N]); //计算雅克比矩阵yy[N][N]
    void inv_jacobian(double yy[N][N],double inv[N][N]); //计算雅克比矩阵的逆矩阵inv
    void newdundiedai(double x0[N], double inv[N][N],double y0[N],double x1[N]); //由近似解向量 x0 计算近似解向量 x1

    //    double x0[N]={82.7995,-5.92913,361.667};
    double x0[N]={-5,-6,-7};

    double y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm;
    int i,j,iter=0;

    cout<<"初始近似解向量："<<endl;
    for (i=0;i<N;i++)
        cout<<x0[i]<<"  ";
    cout<<endl;cout<<endl;
    do
    {
        iter=iter+1;
        cout<<"第 "<<iter<<" 次迭代开始"<<endl;

        //计算向量函数的因变量向量 y0

        ff(x0,y0);//double aaa = exp(-5);

        //计算雅克比矩阵 jacobian
        ffjacobian(x0,jacobian);

        //计算雅克比矩阵的逆矩阵 invjacobian
        inv_jacobian(jacobian,invjacobian);

        //由近似解向量 x0 计算近似解向量 x1

        newdundiedai(x0, invjacobian,y0,x1);

        //计算差向量的1范数errornorm
        errornorm=0;
        for (i=0;i<N;i++)
            errornorm=errornorm+fabs(x1[i]-x0[i]);
        if (errornorm<Epsilon) break;

        for (i=0;i<N;i++)
            x0[i]=x1[i];

    } while (iter<Max);

    return 0;
}

void ff(double xx[N],double yy[N])
{
    double x,y,z;
    int i;

    x=xx[0];
    y=xx[1];
    z=xx[2];

    //    yy[0]=3*x-2*y+4*z-11;
    //    yy[1]=2*x*x+2*x+y*y+3*y+4*z*z-27;
    //    yy[2]=x+2*y+3*z-14;

    yy[0]=3*x-cos(y*z)-0.5;
    yy[1]=x*x-81*(y+0.1)*(y+0.1)+sin(z)+1.06;
    yy[2]=exp(-x*y)+20*z+10.0/3.0*3.14159-1;


    cout<<"向量函数的因变量向量是： "<<endl;
    for( i=0;i<N;i++)
        cout<<yy[i]<<"  ";
    cout<<endl;
    cout<<endl;
}

void ffjacobian(double xx[N],double yy[N][N])
{
    double x,y,z;
    int i,j;

    x=xx[0];
    y=xx[1];
    z=xx[2];
    //jacobian have n*n element
    //    yy[0][0]=2*x-2;
    //    yy[0][1]=-1;
    //    yy[1][0]=2*x;
    //    yy[1][1]=8*y;

    //    yy[0][0]=3;
    //    yy[0][1]=-2;
    //    yy[0][2]=4;

    //    yy[1][0]=4*x+2;
    //    yy[1][1]=2*y+3;
    //    yy[1][2]=8*z;

    //    yy[2][0]=1;
    //    yy[2][1]=2;
    //    yy[2][2]=3;

    yy[0][0]=3;
    yy[0][1]=sin(y*z)*z;
    yy[0][2]=0;

    yy[1][0]=2*x;
    yy[1][1]=-81*2*(y+0.1);
    yy[1][2]=cos(z);

    yy[2][0]=exp(-x*y)*(-y);
    yy[2][1]=exp(-x*y)*(-x);
    yy[2][2]=20;

    cout<<"雅克比矩阵是： "<<endl;
    for( i=0;i<N;i++)
    {for(j=0;j<N;j++)
            cout<<yy[i][j]<<"  ";
        cout<<endl;
    }
    cout<<endl;
}

void inv_jacobian(double yy[N][N],double inv[N][N])
{
    double aug[N][N2],L;
    int i,j,k;

    cout<<"开始计算雅克比矩阵的逆矩阵 ："<<endl;
    for (i=0;i<N;i++)
    {  for(j=0;j<N;j++)
            aug[i][j]=yy[i][j];
        for(j=N;j<N2;j++)
            if(j==i+N) aug[i][j]=1;
            else  aug[i][j]=0;
    }
    for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
            cout<<aug[i][j]<<"  ";
        cout<<endl;
    }
    cout<<endl;

    for (i=0;i<N;i++)
    {
        for (k=i+1;k<N;k++)
        {L=-aug[k][i]/aug[i][i];
            for(j=i;j<N2;j++)
                aug[k][j]=aug[k][j]+L*aug[i][j];
        }
    }

    for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
            cout<<aug[i][j]<<"  ";
        cout<<endl;
    }
    cout<<endl;

    for (i=N-1;i>0;i--) -0
    {
        for (k=i-1;k>=0;k--)
        {L=-aug[k][i]/aug[i][i];
            for(j=N2-1;j>=0;j--)
                aug[k][j]=aug[k][j]+L*aug[i][j];
        }
    }
    for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
            cout<<aug[i][j]<<"  ";
        cout<<endl;
    }
    cout<<endl;
    for (i=N-1;i>=0;i--)
        for(j=N2-1;j>=0;j--)
            aug[i][j]=aug[i][j]/aug[i][i];

    for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
            cout<<aug[i][j]<<"  ";
        cout<<endl;
        for(j=N;j<N2;j++)
            inv[i][j-N]=aug[i][j];
    }
    cout<<endl;

    cout<<"雅克比矩阵的逆矩阵： "<<endl;
    for (i=0;i<N;i++)
    {  for(j=0;j<N;j++)
            cout<<inv[i][j]<<"  ";
        cout<<endl;
    }
    cout<<endl;
}

void newdundiedai(double x0[N], double inv[N][N],double y0[N],double x1[N])
{
    int i,j;
    double sum=0;

    for(i=0;i<N;i++)
    { sum=0;
        for(j=0;j<N;j++)
            sum=sum+inv[i][j]*y0[j];
        x1[i]=x0[i]-sum;
    }
    cout<<"近似解向量："<<endl;
    for (i=0;i<N;i++)
        cout<<x1[i]<<"  ";
    cout<<endl;cout<<endl;
}

牛顿法的算法步骤：

其实看懂了就很简单：就是要求两个矩阵。雅克比矩阵及其逆矩阵。雅克比矩阵就是上图，雅克比矩阵就是偏导数，求完雅克比矩阵，矩阵里面元素都是常数了，就是再去求这个常数矩阵的逆矩阵，求逆矩阵代码一大把。

再给出刚开始代码链接里面一个二元二次方程组的例子的源代码：

//经典牛顿迭代法C++实现
#include<iostream>
#include<cmath>
#define N 2               // 非线性方程组中方程个数、未知量个数
#define Epsilon 0.0001    // 差向量1范数的上限
#define Max     100       //最大迭代次数
using namespace std;
const int N2=2*N;
int main()
{
void ff(float xx[N],float yy[N]); //计算向量函数的因变量向量yy[N]
void ffjacobian(float xx[N],float yy[N][N]); //计算雅克比矩阵yy[N][N]
void inv_jacobian(float yy[N][N],float inv[N][N]); //计算雅克比矩阵的逆矩阵inv
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]); //由近似解向量 x0 计算近似解向量 x1

float x0[N]={12.0,10.25},y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm;
int i,j,iter=0;

//如果取消对x0的初始化，撤销下面两行的注释符，就可以由键盘向x0读入初始近似解向量
//for( i=0;i<N;i++)
//      cin>>x0[i];

cout<<"初始近似解向量："<<endl;
    for (i=0;i<N;i++)
cout<<x0[i]<<"  ";
    cout<<endl;cout<<endl;
do
{
    iter=iter+1;
    cout<<"第 "<<iter<<" 次迭代开始"<<endl;

//计算向量函数的因变量向量 y0

ff(x0,y0);

//计算雅克比矩阵 jacobian

ffjacobian(x0,jacobian);

//计算雅克比矩阵的逆矩阵 invjacobian
inv_jacobian(jacobian,invjacobian);

//由近似解向量 x0 计算近似解向量 x1

newdundiedai(x0, invjacobian,y0,x1);

//计算差向量的1范数errornorm
    errornorm=0;
    for (i=0;i<N;i++)
        errornorm=errornorm+fabs(x1[i]-x0[i]);
    if (errornorm<Epsilon) break;

    for (i=0;i<N;i++)
        x0[i]=x1[i];

} while (iter<Max);

return 0;
}

void ff(float xx[N],float yy[N])
{float x,y;
 int i;

    x=xx[0];
    y=xx[1];

    yy[0]=x*x-2*x-y+0.5;
    yy[1]=x*x+4*y*y-4;

    cout<<"向量函数的因变量向量是： "<<endl;
    for( i=0;i<N;i++)
      cout<<yy[i]<<"  ";
    cout<<endl;
    cout<<endl;

}

void ffjacobian(float xx[N],float yy[N][N])
{
  float x,y;
  int i,j;

    x=xx[0];
    y=xx[1];
    //jacobian have n*n element
    yy[0][0]=2*x-2;
    yy[0][1]=-1;
    yy[1][0]=2*x;
    yy[1][1]=8*y;

   cout<<"雅克比矩阵是： "<<endl;
    for( i=0;i<N;i++)
   {for(j=0;j<N;j++)
         cout<<yy[i][j]<<"  ";
       cout<<endl;
   }
    cout<<endl;
}

void inv_jacobian(float yy[N][N],float inv[N][N])
{float aug[N][N2],L;
 int i,j,k;

 cout<<"开始计算雅克比矩阵的逆矩阵 ："<<endl;
 for (i=0;i<N;i++)
    {  for(j=0;j<N;j++)
         aug[i][j]=yy[i][j];
       for(j=N;j<N2;j++)
        if(j==i+N) aug[i][j]=1;
        else  aug[i][j]=0;
    }


 for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
         cout<<aug[i][j]<<"  ";
       cout<<endl;
    }
cout<<endl;


for (i=0;i<N;i++)
    {
      for (k=i+1;k<N;k++)
      {L=-aug[k][i]/aug[i][i];
        for(j=i;j<N2;j++)
         aug[k][j]=aug[k][j]+L*aug[i][j];
      }
    }


 for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
         cout<<aug[i][j]<<"  ";
       cout<<endl;
    }
cout<<endl;


 for (i=N-1;i>0;i--)
    {
     for (k=i-1;k>=0;k--)
      {L=-aug[k][i]/aug[i][i];
        for(j=N2-1;j>=0;j--)
         aug[k][j]=aug[k][j]+L*aug[i][j];
      }
    }




for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
         cout<<aug[i][j]<<"  ";
       cout<<endl;
    }
cout<<endl;


for (i=N-1;i>=0;i--)
   for(j=N2-1;j>=0;j--)
        aug[i][j]=aug[i][j]/aug[i][i];


for (i=0;i<N;i++)
    {  for(j=0;j<N2;j++)
         cout<<aug[i][j]<<"  ";
       cout<<endl;
       for(j=N;j<N2;j++)
       inv[i][j-N]=aug[i][j];
    }
cout<<endl;


cout<<"雅克比矩阵的逆矩阵： "<<endl;
for (i=0;i<N;i++)
    {  for(j=0;j<N;j++)
         cout<<inv[i][j]<<"  ";
       cout<<endl;
    }
cout<<endl;

}

void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N])
{
    int i,j;
    float sum=0;

    for(i=0;i<N;i++)
    { sum=0;
      for(j=0;j<N;j++)
        sum=sum+inv[i][j]*y0[j];
        x1[i]=x0[i]-sum;
    }
    cout<<"近似解向量："<<endl;
    for (i=0;i<N;i++)
     cout<<x1[i]<<"  ";
    cout<<endl;cout<<endl;
}

不过，弄好了是简单，这段代码也消耗了我一天的时间，首先是看原理，因为上学的时候只记得电力系统计算潮流那段有个叫雅克比矩阵的东东的，至于是干嘛用的，完全忘记了，当时只应付考试了。看完原理然后就是代码，有的代码是错的，调试半天也不行。