递归算法的三个分解步骤

递归是一个重要的算法，希望你也能学得会。

递归的三大步骤

编写递归函数的步骤，可以分解为三个。

递归第一个步骤：明确函数要做什么

对于递归，一个最重要的事情就是要明确这个函数的功能。这个函数要完成一样什么样的事情，是完全由程序员来定义的，当写一个递归函数的时候，先不要管函数里面的代码是什么，而要先明确这个函数是实现什么功能的。

比如，我定义了一个函数，这个函数是用来计算n的阶乘的。

// 计算n的阶乘（假设n不为0）
int f(int n) {
    // 先不管内部实现逻辑
}

这样，就完成了第一个步骤：明确递归函数的功能。

递归第二个步骤：明确递归的结束（退出递归）条件

所谓递归，就是会在函数的内部逻辑代码中，调用这个函数本身。因此必须在函数内部明确递归的结束（退出）递归条件，否则函数会一直调用自己形成死循环。意思就是说，需要有一个条件（标识符参数）去引导递归结束，直接将结果返回。要注意的是，这个标识符参数需要是可以预见的，对于函数的执行返回结果也是可以预见的。

比如在上面的计算n的阶乘的函数中，当n=1的时候，肯定能知道f(n)对应的结果是1，因为1的阶乘就是1，那么我们就可以接着完善函数内部的逻辑代码，即将第二元素（递归结束条件）加进代码里面。

// 计算n的阶乘（假设n不为0）
int f(int n) {
    if (n == 1) {
        return 1;
    }
}

当然了，当n=2的时候，也可以知道n的阶乘是2，那么也可以把n=2作为递归的结束条件。

// 计算n的阶乘（假设n>=2）
int f(int n) {
    if (n == 2) {
        return 2;
    }
}

这里就可以看出，递归的结束条件并不局限，只要递归能正常结束，任何结束条件都是允许的，但是要注意一些逻辑上的细节。比如说上面的n==2的条件就需要n>2，否则当n=1的时候就会被漏掉，可能导致递归不能正常结束。完善一下就是当n<=2的时候，f(n)都会等于n。

// 计算n的阶乘（假设n不为0）
int f(int n) {
    if (n <= 2) {
        return n;
    }
}

这样，就完成了第二步骤：明确递归的退出条件。

递归的第三个步骤：找到函数的等价关系式

递归的第三个步骤就是要不断地缩小参数的范围，缩小之后就可以通过一些辅助的变量或操作使原函数的结果不变。比如在上面的计算n的阶乘的函数中，要缩小f(n)的范围，就可以让f(n)=n* f(n-1)，这样范围就从n变成了n-1，范围变小了，直到范围抵达n<=2退出递归。并且为了维持原函数不变，我们需要让f(n-1)乘上n。说白了，就是要找到一个原函数的等价关系式。在这里，f(n)的等价关系式为n*f(n-1)，即f(n)=n*f(n-1)。

// 计算n的阶乘（假设n不为0）
int f(int n) {
    if (n <= 2) {
        return n;
    }
    // 把n打出来看一下，你就能明白递归的原理了
    System.out.println(n);
    // 加入f(n)的等价操作逻辑
    return n * f(n - 1);
}

到这里f(n)的功能就基本实现了。每次写递归函数的时候，强迫自己跟着这三个步骤走，能达到事半功倍的效果。另外也可以看出，第三个步骤几乎是最难的一个步骤。

递归案例1：斐波那契数列

斐波那契数列的是这样一个数列：1、1、2、3、5、8、13、21、34、….，即第一项 f(1) = 1、第二项 f(2) = 1、…..、第 n 项目为 f(n)=f(n-1)+f(n-2)，求第 n 项的值是多少。

递归第一个步骤：明确函数要做什么

假设f(n)的功能是求第n项的值，代码如下：

int f(int n) {
    
}

递归第二个步骤：明确递归的结束（退出递归）条件

显然，当n=1或者n=2的时候，我们可以轻易得知结果是f(1)=f(2)=1。所以递归结束的条件可以是n<=2，代码如下：

int f(int n) {
    if (n <= 2) {
        return 1;
    }
}

递归的第三个步骤：找到函数的等价关系式

在题目中已经有等价关系式了，即f(n) = f(n-1) + f(n-2)。

int f(int n) {
    // 先写递归结束条件
    if (n <= 2) {
        return 1;
    }
    // 写等价关系式
    return f(n - 1) + f(n - 2);
}

这个案例非常简单。

递归案例2：小青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。

递归第一个步骤：明确函数要做什么

假设f(n)的功能是求青蛙跳上一个n级台阶总共有多少种跳法，代码如下：

int f(int n) {

}

递归第二个步骤：明确递归的结束（退出递归）条件

上面说了，求递归结束的条件，直接把n压缩到很小很小就行了，因为n越小我们就能越直观地算出f(n)的多少。这里，当n=1的时候，f(1)=1，因此可以将n=1作为递归结束条件。

int f(int n) {
    if (n == 1) {
        return 1;
    }
}

递归的第三个步骤：找到函数的等价关系式

接下来找到函数的等价关系式就是这个函数的难点了，下面来分析一下。

1.假设台阶只有一级，那么显然只有一种跳法。

2.要是有两级台阶，那么就有两种跳法：一种是一次跳一级台阶，一种是一次跳两级台阶。

3.要是有三级台阶，青蛙的第一步就有两种跳法：当青蛙第一步跳了一级台阶，那么就只剩下了两级台阶，将问题转化成为两级台阶的跳法，当青蛙第一步跳了两级台阶，那么就只剩下了一级台阶，就将问题转化为了一级台阶的跳法。

4.n阶台阶与三阶台阶的分析是一样的。

我们把跳n级台阶时的跳法看成是n的函数，记为f(n)。当n=1时，f(1)=1；当n=2时，f(2)=2；当n=3时，f(3)=f(2)+f(1)；当n=4时，f(4)=f(3)+f(2)......当n=n的时候，f(n)=f(n-2)+f(n-1)，显然这是一个斐波那契数列。

int f(int n) {
    // 先写递归结束条件
    if (n == 1) {
        return 1;
    }
    // 写等价关系式
    return f(n - 1) + f(n - 2);
}

要注意的是，上面的递归结束条件显然不够严谨，因为当n=2的时候，这里的递归退出条件就不能够限制递归的正常退出了，需要稍微完善一下。

int f(int n) {
    // 先写递归结束条件
    if (n < 1) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    // 写等价关系式
    return f(n - 1) + f(n - 2);
}

因此建议在写完递归函数之后要回头去校验递归退出条件。

递归案例3：反转单链表

反转单链表是一个常见的算法。例如链表为1->2->3->4。反转后为 4->3->2->1。

链表的节点定义如下：

class Node {
    int date;
    Node next; // 存储下一个节点
}

递归第一个步骤：明确函数要做什么

假设函数reverseList(head)的功能是反转单链表，其中head表示链表的头节点。代码如下：

Node reverseList(Node head) {

}

递归第二个步骤：明确递归的结束（退出递归）条件

当链表只有一个节点，或者如果是空链表的话，就直接返回head就行了。

Node reverseList(Node head) {
    if (head == null || head.next == null){
        return head;
    }
}

递归的第三个步骤：找到函数的等价关系式

// 用递归的方法反转链表
public static Node reverseList2(Node head) {
        // 递归结束条件
        if (head == null || head.next == null) {
            return head;
        }
        // 递归反转子链表
        Node newList = reverseList2(head.next);
        // 改变1，2节点的指向
        // 通过head.next获取节点2
        Node t1  = head.next;
        // 让2的next指向 2
        t1.next = head;
        // 1的next指向null
        head.next = null;
        // 把调整之后的链表返回
        return newList;
}

递归的一些优化思路

递归的优化也是一门学问，这里列出两个优化思路。

考虑是否重复计算

递归的时候很可能会出现子运算重复计算的问题。什么是子运算？f(n-1)，f(n-2)等就是子运算。

例如，在上面的案例中，等价表达式是f(n)=f(n-1)+f(n-2)，递归调用的状态图如下：

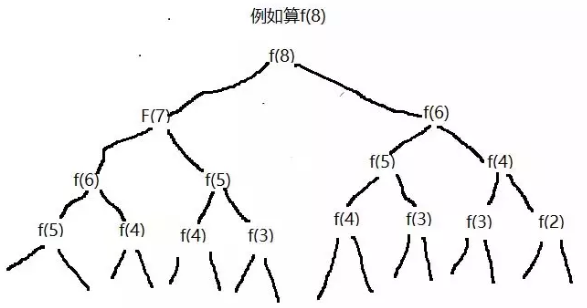
可以看出，在递归调用的时候，重复计算了两次f(5)，五次f(4)等......这时非常恐怖的，因为n越大，重复计算的就越多，因此必须想办法优化。

如何优化呢，一般的做法是把计算的结果保存起来，例如把f(4)的结果保存起来，当再次要计算f(4)的时候，先判断一下之前是否计算过，计算过就可以直接取结果了。用什么保存呢，可以用数组或者HashMap保存，这里用数组保存好了。把n作为数组下标，f(n)作为值，例如arr[n]=f(n)这样子。当f(n)还没有计算过的时候，我们让arr[n]等于一个特殊值，例如arr[n]=-1。当我们要判断的时候，如果arr[n]=-1，则证明f(n)没有计算过，否则，f(n)就已经计算过了，且f(n)=arr[n]。

// 假定arr数组已经初始化好
int f(int n) {
    if (n <= 1) {
        return n;
    }
    // 先判断有没计算过
    if (arr[n] != -1) {
        // 计算过，直接返回
        return arr[n];
    } else {
        // 没有计算过，递归计算,并且把结果保存到 arr数组里
        arr[n] = f(n - 1) + f(n - 1);
        reutrn arr[n];
    }
}

也就是说，使用递归的时候，必须要考虑有没有重复计算，如果重复计算了，一定要把计算过的状态值保存起来。

考虑是否可以自底向上

对于递归，一般的思路是从上往下递归，直到递归到达最底层，再一层一层地把值返回。

这样的话，在n比较大的情况下，比如当n=10000的时候，就必须要往下递归10000层直到n<=1的时候才开始将结果逐层返回，可能会导致栈空间不够用而报出StackOverflowException的异常。

对于这种情况就可以考虑自底向上递归的做法。

int f (int n) {
    if (n <= 2) {
        return n;
    }
    
    int f1 = 1;
    int f2 = 2;
    int sum = 0;
    
    for (int i = 3; i <= n; i++) {
        sum = f1 + f2;
        f1 = f2;
        f2 = sum;
    }
    
    return sum;
}

另外的，这种方法也可以被称为递推。

总结

其实递归并不一定总是从上往下，也有很多从下往上的写法。比如可以从n=1开始，一直递归到n=1000，常用在一些排序组合的场景。而对于这种从下往上的写法，也是有相应的优化技巧。

最后要说的是，对于递归这种比较抽象的思想，需要自己多思考和多写才能对较好地掌握递归，可能要秃头才敢说对递归熟练吧（手动滑稽）。

 

"就这样吧，再坏的也不要走了，再好的也不要来了。"