红黑树入门

红黑树实际上是一种自平衡二叉查找树。

二叉树

二叉树是每个节点最多有两个子树的树结构，每个节点都可以用于存储数据，可以由任1个节点访问它的左右子树或者父节点。

二叉查找树

二叉查找树或者是一颗空树，或者是具有下列性质的二叉树：

1.每个节点都有一个作为查找依据的关键码（key），所有的节点的关键码互不相同（唯一）。

2.左子树（如果存在）上所有节点的关键码都小于根节点的关键码。

3.右子树（如果存在）上所有节点的关键码都大于根节点的关键码。

4.左子树和右子树也是二叉查找树。

 

这样，一棵二叉查找树的所有元素节点都是有序的。在二叉树的形态比较平衡的情况下，它的检索效率很高，有点类似于二分法检索有序数组的效率。一般情况下，查询复杂度是与目标节点到根节点的距离（即深度）有关的。然而，不断地添加、删除节点，可能造成二叉查找树形态非常不平衡，在极端情形下它会变成单链表，检索效率也就会变得低下。

下图就是二叉查找树在极端情形下变成单链表的例子：

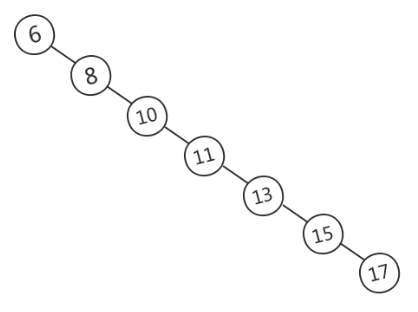
自平衡二叉查找树

什么是自平衡二叉查找树？在不断地向二叉查找树中添加、删除节点时，二叉查找树自身通过形态地变换，始终保持着这一定程度上的平衡，即为自平衡二叉树。自平衡二叉查找树只是一个概念，它有许多种不同的实现方式，如AVL树和红黑树。

红黑树

红黑树是一种自平衡性较好的二叉查找树，它在Linux内核、C++的STL库等许多场合下都作为核心数据结构使用。红黑树容器中的元素都是有序的，它支持快速的检索、插入、删除操作，也支持范围查询、遍历等操作，是一种应用场景非常广泛的高级数据结构。

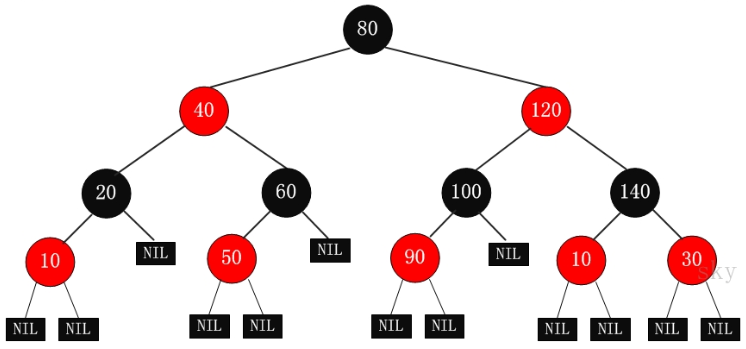
红黑树实际是指每个节点都带有颜色属性的二叉查找树，其中颜色为红色或黑色。除了二叉查找树的一般要求外，对于红黑树还有如下的额外的特性。

1.节点是红色或黑色。

2.根节点是黑色。

3.所有的叶子节点都是黑色（叶子是NIL节点，也叫"哨兵"）。

4.每个红色节点的两个子节点都是黑色（每个叶子节点到根节点的所有路径上不能有两个连续的红色节点）。

5.从任一节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点。

这些约束加强了红黑树的关键性质：从根节点到叶子节点的最长可能路径长度不大于最短可能路径的两倍，这样这个树大致上就是平衡的了。因为二叉树的操作（比如插入、删除和查找某个值的最慢时间）都是与树的高度成比例的，以上的5个特性保证了树的高度（最长路径），所以它完全不同于普通的二叉查找树。

这些特性为什么可以导致上述结果呢？因为特性4实际上决定了1个路径不能有两个毗邻的红色节点，这一点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色节点和黑色节点。根据特性5可知，所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能大于其他路径长度的两倍。

 

"敏感细腻的人，总要比一般人走更远更长的路，才能认清自己。"