第三章 - 有穷自动机与词法分析（二）

3.2 有穷自动机

自动机一方面是单词的描述工具，另一方面可以比较容易构造出识别器程序。

有穷自动机FA分为（非确定有穷自动机NFA）和（确定有穷自动机DFA）

3.2.1 确定有穷自动机

包含以下五部分：

【1】符号集∑（输入符号集）

【2】状态集合SS = {S0,S1,S2,S3,...,Sn}

【3】开始状态S0

【4】终止（接受）状态集： {S0,S1,S2,S3,...,Sn}

【5】状态转换器

 

自动机定义方式主要包括（图形法）、（转换表法）和（函数法）

【函数法】下面是一个有穷自动机，接受所有以‘a’开头并由‘a’、0、1符号组成的符号串（可以没有0、1部分）

【1】符号集∑={0、1、‘a’}

【2】状态集合SS = {S0,S1}

【3】开始状态S0

【4】终止（接受）状态集： {S1}

【5】状态转换函数。。。。。

【表格法】

【图形法】

被动机接受 及一些特殊例子

 

3.2.2 确定有穷自动机的实现

有穷自动机用于构造词法分析器Scanner。下面考虑DFA的实现，一种是（面向状态转换表）的方法，一种是（面向状态转换图）的方法。

 

3.2.3 非确定有穷自动机

区别主要有三点：

①一个状态的不同输出边可标有相同的符号

②允许有多个开始状态

③允许有ε边

 

3.2.4 NFA到DFA的转换

转化时把ε边删除

【ε-闭包】如图：

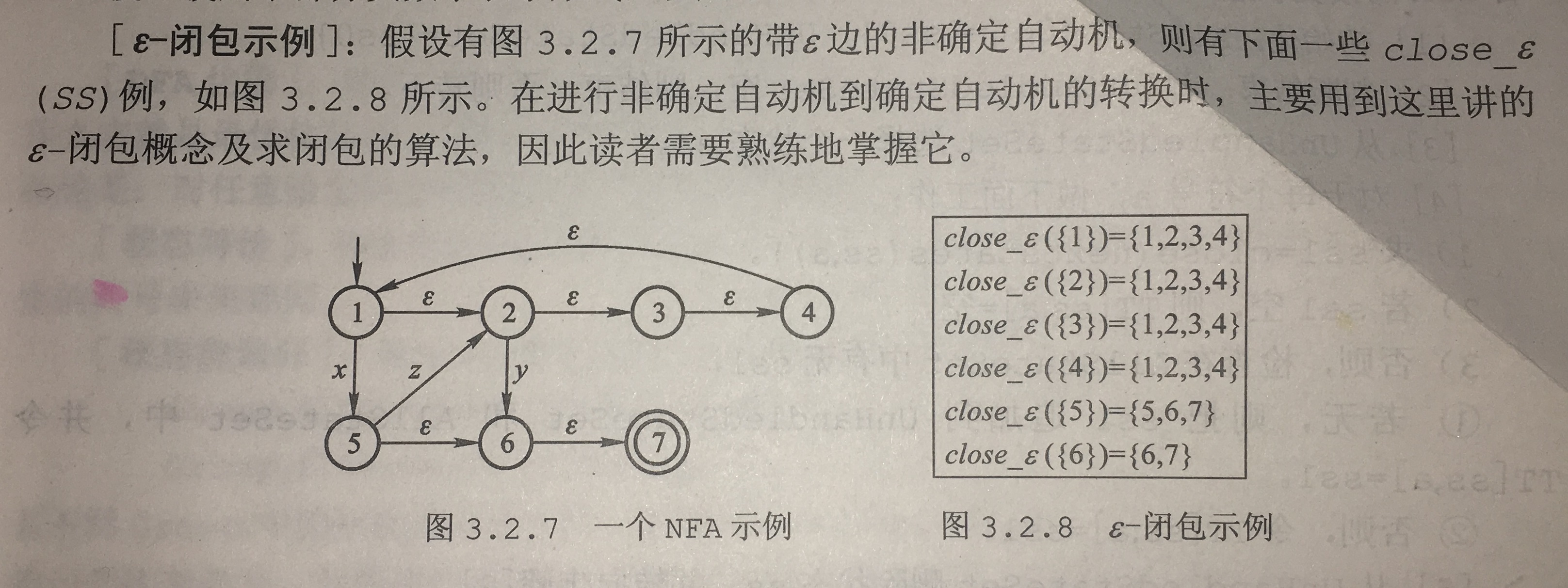
转化原理：DFA的状态被表示为NFA的状态之集  --用SS（状态集）的形式表示DFA

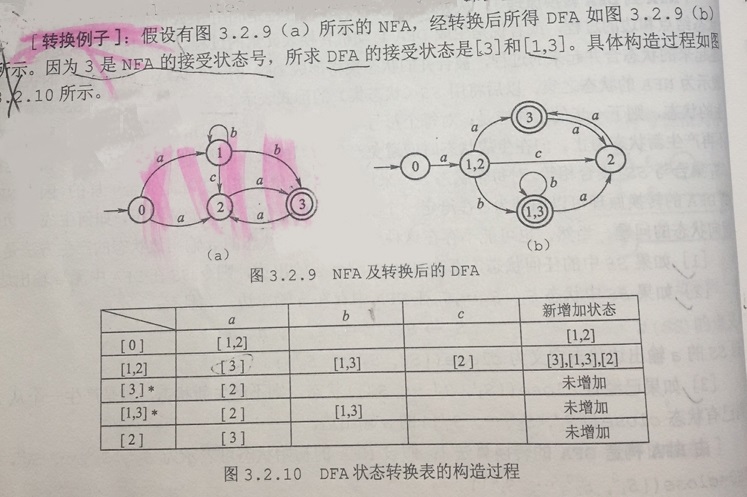
3.2.5 确定有穷自动机的极小化

【DFA化简】减少状态个数到最少

【状态等价】称有穷自动机两个状态等价，当且仅当他们从他们到接受状态产生的符号串集相同。

【状态集划分】

【初始划分】

【异类状态】

【分裂】

3.2.6 自动机状态转换表的实现

词法分析器

词法分析器是使用频度很高的程序段，提高其速度是非常重要的事情。

对应的实现方法：全查法（节省空间速度慢），不查法即索引法（占用空间大但是速度慢），半查法（折中）