课程1-神经网络和深度学习—第3周-带有一个隐藏层的平面数据分类
题目
- 要建立一个神经网络，它有一个隐藏层。该模型可以对图中的散点（二分类）绘制出决策边界。
- 这个模型和上一个逻辑回归实现的模型有很大的区别。testCases.py和planar_utils.py的完整代码也在最底部。
- 在这篇文章中有如下知识：
- 构建具有单隐藏层的2类分类神经网络。
- 使用具有非线性激活功能激活函数，例如tanh。
- 计算交叉熵损失（损失函数）。
- 实现向前和向后传播。
编程实现
1. 准备软件包
- 我们需要准备一些软件包：
- numpy：是用Python进行科学计算的基本软件包。
- matplotlib ：是一个用于在Python中绘制图表的库。
- sklearn：为数据挖掘和数据分析提供的简单高效的工具。
- testCases：提供了一些测试示例来评估函数的正确性，参见底部的代码。
- planar_utils ：提供了在这个任务中使用的各种有用的功能函数，参见底部的代码。
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
#%matplotlib inline #如果你使用用的是Jupyter Notebook的话请取消注释。
np.random.seed(1) #设置一个固定的随机种子，以保证接下来的步骤中我们的结果是一致的。
2. 加载和查看数据集
首先，我们来看看我们将要使用的数据集，下面的代码会将一个花的图案的2类数据集加载到变量X和Y中
X, Y = load_planar_dataset()
把数据集加载完成了，然后使用matplotlib可视化数据集，代码如下：
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y),s=40,cmap=plt.cm.Spectral) #绘制散点图
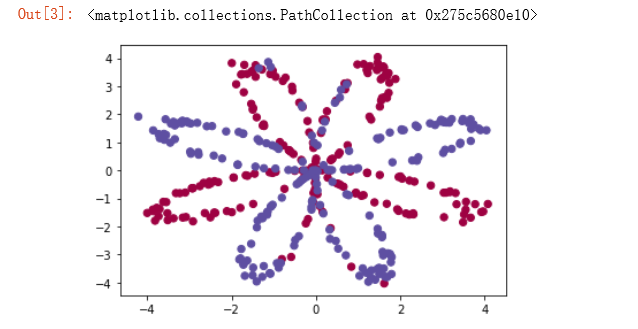
数据看起来像一朵红色（y = 0）和一些蓝色（y = 1）的数据点的花朵的图案。 我们的目标是建立一个模型来适应这些数据。现在，我们已经有了以下的东西：
- X：一个numpy的矩阵，包含了这些数据点的数值
- Y：一个numpy的向量，对应着的是X的标签【0 | 1】（红色:0 ， 蓝色 :1）
shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1] # 训练集里面的数量
print ("X的维度为: " + str(shape_X))
print ("Y的维度为: " + str(shape_Y))
print ("数据集里面的数据有：" + str(m) + " 个")
3. 查看简单的Logistic回归的分类效果
在构建完整的神经网络之前，先让我们看看逻辑回归在这个问题上的表现如何，我们可以使用sklearn的内置函数来做到这一点，运行下面的代码来训练数据集上的逻辑回归分类器。
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)
把逻辑回归分类器的分类绘制出来：
plot_decision_boundary(lambda x: clf.predict(x), X, np.squeeze(Y)) #绘制决策边界
plt.title("Logistic Regression") #图标题
LR_predictions = clf.predict(X.T) #预测结果
print ("逻辑回归的准确性： %d " % float((np.dot(Y, LR_predictions) + np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) + "% " + "(正确标记的数据点所占的百分比)")
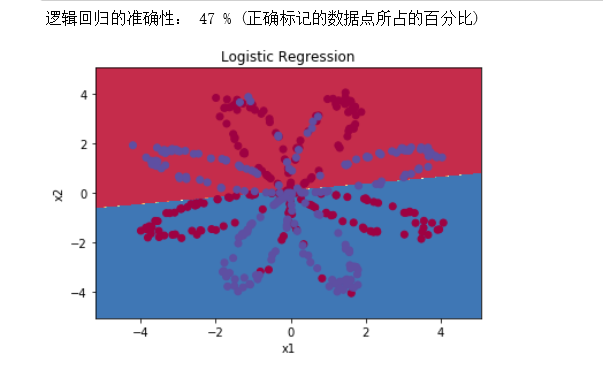
这里遇到了一点问题参考这个博客得以解决。
准确性只有47%的原因是数据集不是线性可分的，所以逻辑回归表现不佳，现在我们正式开始构建神经网络。
4. 搭建神经网络
要搭建的神经网络模型如下图：
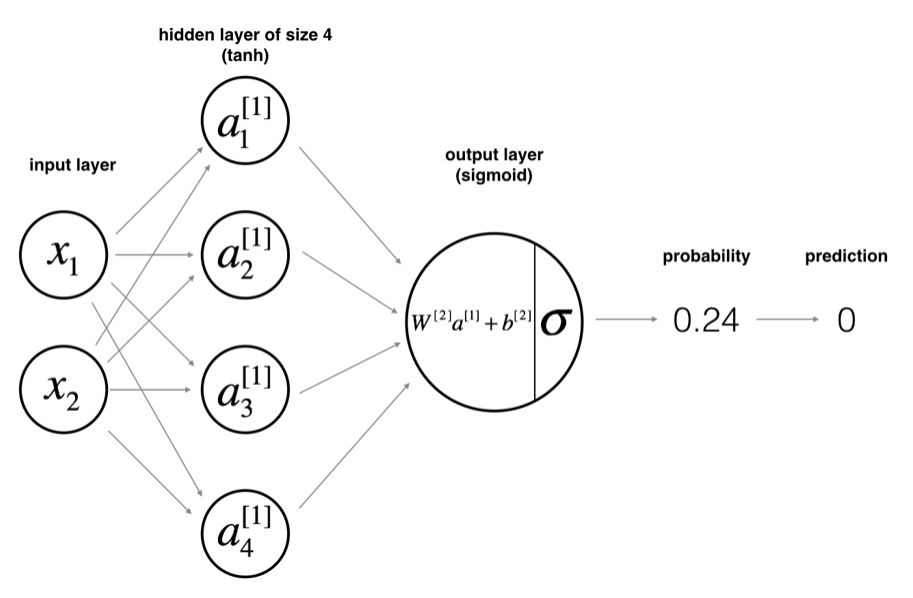
对于 \(x^{(i)}\)（第i个训练样本）而言:
注： \(a^{[2](i)}\) ，其中[2]指第二层，(i)指第i个训练样本。其他符号同理。
\[z^{[1](i)}=w^{[1](i)} x^{(i)} + b^{[1](i)} \tag{1}
\]
\[a^{[1](i)}=tanh(z^{[1](i)}) \tag{2}
\]
\[z^{[2](i)}=w^{[2](i)} a^{[1](i)} + b^{[2](i)} \tag{3}
\]
\[a^{[2](i)}=\sigma(z^{[2](i)}) \tag{4}
\]
向量化实现：
\[Z^{[1]}=W^{[1]} X + b^{[1]} \tag{6}
\]
\[A^{[1] }=tanh(Z^{[1]}) \tag{7}
\]
\[Z^{[2] }=W^{[2] } A^{[1] } + b^{[2] } \tag{8}
\]
\[A^{[2] }=\sigma(Z^{[2]}) \tag{9}
\]
可以按如下方式计算成本J：
\[J=-\frac1m \sum_{i=1}^m \left( y^{(i)} log(a^{[2](i)}) +(1-y^{(i)}) log(1-a^{[2](i)}) \right) \tag{5}
\]
- 构建神经网络的一般方法是：
- 定义神经网络结构（输入单元的数量，隐藏单元的数量等）
- 初始化模型的参数
- 循环：
- 实施前向传播
- 计算损失
- 实现向后传播
- 更新参数（梯度下降）
- 最后把它们合并到一个nn_model()函数中，当构建好了nn_model（）并学习了正确的参数，就可以预测新的数据。
4.1 定义神经网络结构
- 在构建之前，我们要先把神经网络的结构给定义好：
- n_x: 输入层的数量
- n_h: 隐藏层的数量（这里设置为4）
- n_y: 输出层的数量
def layer_sizes(X , Y):
"""
参数：
X - 输入数据集,维度为（输入的数量，训练/测试的数量）
Y - 标签，维度为（输出的数量，训练/测试数量）
返回：
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
n_x = X.shape[0] #输入层
n_h = 4 #隐藏层，硬编码为4
n_y = Y.shape[0] #输出层
return (n_x,n_h,n_y)
来测试一下：
#测试layer_sizes
print("=========================测试layer_sizes=========================")
# 这里的测试数据 X.shape=(5,3),Y.shape=(2,3)
X_asses , Y_asses = layer_sizes_test_case()
(n_x,n_h,n_y) = layer_sizes(X_asses,Y_asses)
print("输入层的节点数量为: n_x = " + str(n_x))
print("隐藏层的节点数量为: n_h = " + str(n_h))
print("输出层的节点数量为: n_y = " + str(n_y))
4.2 初始化模型的参数
要实现函数initialize_parameters()。要确保参数的大小合适，参考上面的神经网络图。
- 随机值初始化权重矩阵。
np.random.randn(a，b)* 0.01来随机初始化一个维度为(a，b)的矩阵。
- 将偏向量初始化为零。
np.zeros((a，b))用零初始化矩阵（a，b）。
def initialize_parameters( n_x , n_h ,n_y):
"""
参数：
n_x - 输入层节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回：
parameters - 包含参数的字典：
W1 - 权重矩阵,维度为（n_h，n_x）
b1 - 偏向量，维度为（n_h，1）
W2 - 权重矩阵，维度为（n_y，n_h）
b2 - 偏向量，维度为（n_y，1）
"""
np.random.seed(2) #指定一个随机种子，以便你的输出与我们的一样。
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
#使用断言确保我的数据格式是正确的
assert(W1.shape == ( n_h , n_x ))
assert(b1.shape == ( n_h , 1 ))
assert(W2.shape == ( n_y , n_h ))
assert(b2.shape == ( n_y , 1 ))
parameters = {"W1" : W1,
"b1" : b1,
"W2" : W2,
"b2" : b2 }
return parameters
测试一下代码：
#测试initialize_parameters
print("=========================测试initialize_parameters=========================")
n_x , n_h , n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x , n_h , n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
4.3 前向传播
- 现在要实现前向传播函数forward_propagation()。可以使用sigmoid()函数，也可以使用np.tanh()函数。
- 步骤如下：
- 使用字典类型的 parameters（它是initialize_parameters() 的输出）检索每个参数。
- 实现向前传播, 计算 \(Z^{[1]}, A^{[1]}, Z^{[2]}\) 和 \(A^{[2]}\) （训练集里面所有例子的预测向量）。
- 反向传播所需的值存储在“cache”中，cache将作为反向传播函数的输入。
def forward_propagation( X , parameters ):
"""
参数：
X - 维度为（n_x，m）的输入数据。
parameters - 初始化函数（initialize_parameters）的输出
返回：
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型变量
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#前向传播计算A2
Z1 = np.dot(W1 , X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2 , A1) + b2
A2 = sigmoid(Z2)
#使用断言确保我的数据格式是正确的
assert(A2.shape == (1,X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return (A2, cache)
测试一下代码：
#测试forward_propagation
print("=========================测试forward_propagation=========================")
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
print(np.mean(cache["Z1"]), np.mean(cache["A1"]), np.mean(cache["Z2"]), np.mean(cache["A2"]))
4.4 计算损失
计算成本的公式如下：
\[J=-\frac1m \sum_{i=1}^m \left( y^{(i)} log(a^{[2](i)}) +(1-y^{(i)}) log(1-a^{[2](i)}) \right) \tag{5}
\]
开始构建计算成本的函数：
def compute_cost(A2,Y,parameters):
"""
计算公式（5）中给出的交叉熵成本，
参数：
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为（1，数量）
parameters - 一个包含W1，B1，W2和B2的字典类型的变量
返回：
成本 - 交叉熵成本给出方程（13）
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
#计算成本
logprobs = logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
cost = - np.sum(logprobs) / m
cost = float(np.squeeze(cost))
assert(isinstance(cost,float))
return cost
测试一下成本函数：
#测试compute_cost
print("=========================测试compute_cost=========================")
A2 , Y_assess , parameters = compute_cost_test_case()
print("cost = " + str(compute_cost(A2,Y_assess,parameters)))
4.5 反向传播
反向传播通常是深度学习中最难（数学意义）部分，这里有反向传播讲座的幻灯片， 由于我们正在构建向量化实现，因此我们将需要使用这下面的六个方程：
为了计算 \(dZ^{[1]}\) ，里需要计算 \(g^{[1]'}(Z^{[1]})\) ，$ g^{[1]}(...)$ 是tanh激活函数，如果 \(a = g^{[1]}(Z)\) 那么 $ g^{[1]'}(Z) = 1-a^2$ 。所以我们需要使用 (1 - np.power(A1, 2)) 来计算 \(g^{[1]'}(Z^{[1]})\)
def backward_propagation(parameters,cache,X,Y):
"""
使用上述说明搭建反向传播函数。
参数：
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”，“A1”，“Z2”和“A2”的字典类型的变量。
X - 输入数据，维度为（2，数量）
Y - “True”标签，维度为（1，数量）
返回：
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads
测试一下反向传播函数：
#测试backward_propagation
print("=========================测试backward_propagation=========================")
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
4.6 更新参数
我们需要使用 (dW1, db1, dW2, db2) 来更新 (W1, b1, W2, b2) 。
更新算法如下：
\[\theta = \theta - \alpha \frac{\partial J }{ \partial \theta }
\]
- $ \alpha$：学习速率
- \(\theta\)：参数
需要选择一个良好的学习速率，
def update_parameters(parameters,grads,learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数：
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回：
parameters - 包含更新参数的字典类型的变量。
"""
W1,W2 = parameters["W1"],parameters["W2"]
b1,b2 = parameters["b1"],parameters["b2"]
dW1,dW2 = grads["dW1"],grads["dW2"]
db1,db2 = grads["db1"],grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
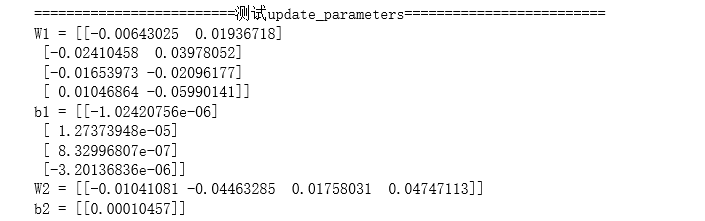
测试一下update_parameters()：
#测试update_parameters
print("=========================测试update_parameters=========================")
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
4.7 整合成一个函数
现在把上面的东西整合到nn_model()中，神经网络模型必须以正确的顺序使用先前的功能。
def nn_model(X,Y,n_h,num_iterations,print_cost=False):
"""
参数：
X - 数据集,维度为（2，示例数）
Y - 标签，维度为（1，示例数）
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True，则每1000次迭代打印一次成本数值
返回：
parameters - 模型学习的参数，它们可以用来进行预测。
"""
np.random.seed(3) # 指定随机种子
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x,n_h,n_y)
# 初始化后的参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 开始循环
for i in range(num_iterations):
A2 , cache = forward_propagation(X,parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters,grads,learning_rate = 1.2)
if print_cost:
if i%1000 == 0:
print("第 ",i," 次循环，成本为："+str(cost))
return parameters
测试nn_model()：
#测试nn_model
print("=========================测试nn_model=========================")
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
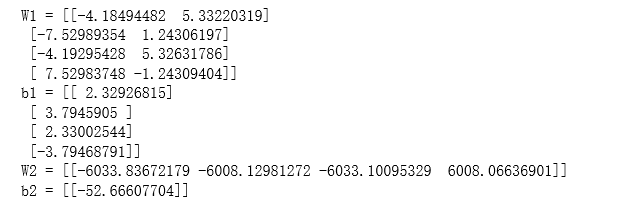
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
4.8 模型预测
构建predict()来使用模型进行预测， 使用向前传播来预测结果。
def predict(parameters,X):
"""
使用学习的参数，为X中的每个示例预测一个类
参数：
parameters - 包含参数的字典类型的变量。
X - 输入数据（n_x，m）
返回
predictions - 我们模型预测的向量（红色：0 /蓝色：1）
"""
A2 , cache = forward_propagation(X,parameters)
# 返回浮点数A2的四舍五入的值
predictions = np.round(A2)
return predictions
进行测试：
#测试predict
print("=========================测试predict=========================")
parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("预测的平均值 = " + str(np.mean(predictions)))
5. 正式运行
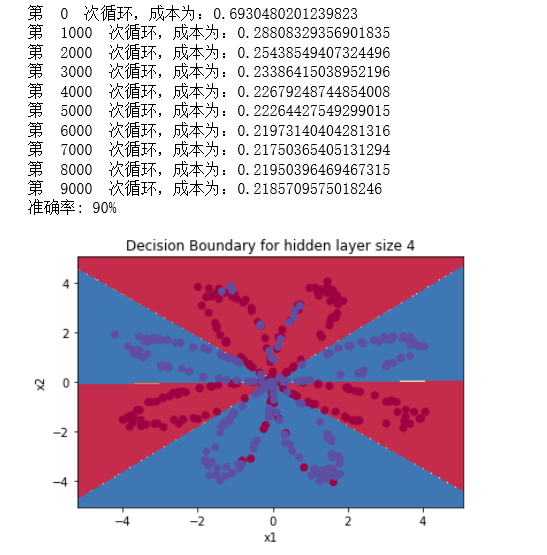
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
6. 更改隐藏层节点数量
上面的实验把隐藏层定为4个节点，现在更改隐藏层里面的节点数量，看一看节点数量是否会对结果造成影响。
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] #隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i + 1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations=5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("隐藏层的节点数量： {} ，准确率: {} %".format(n_h, accuracy))
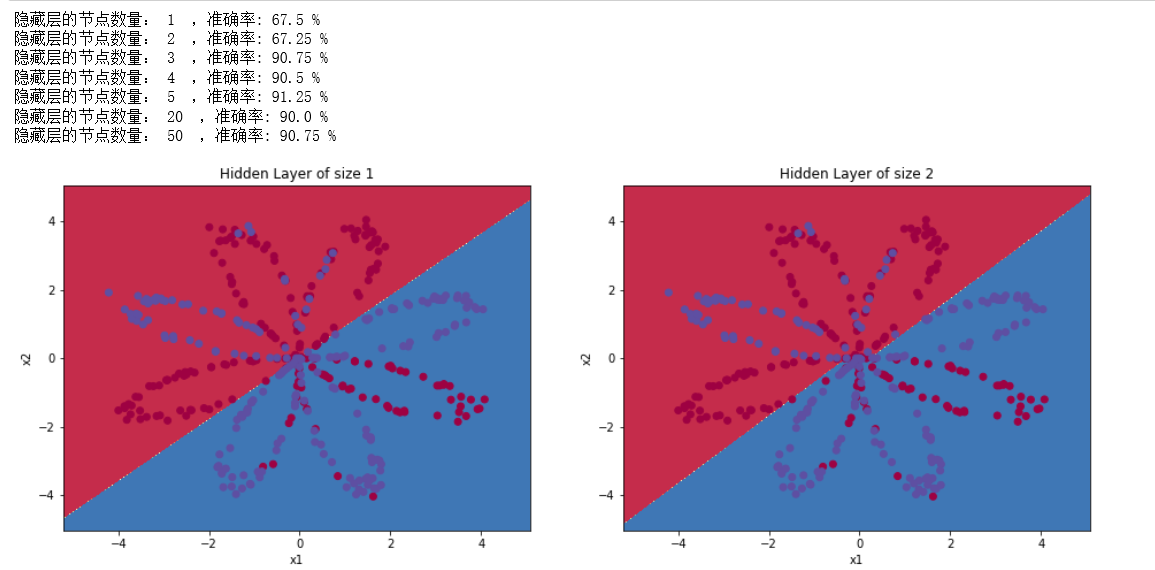
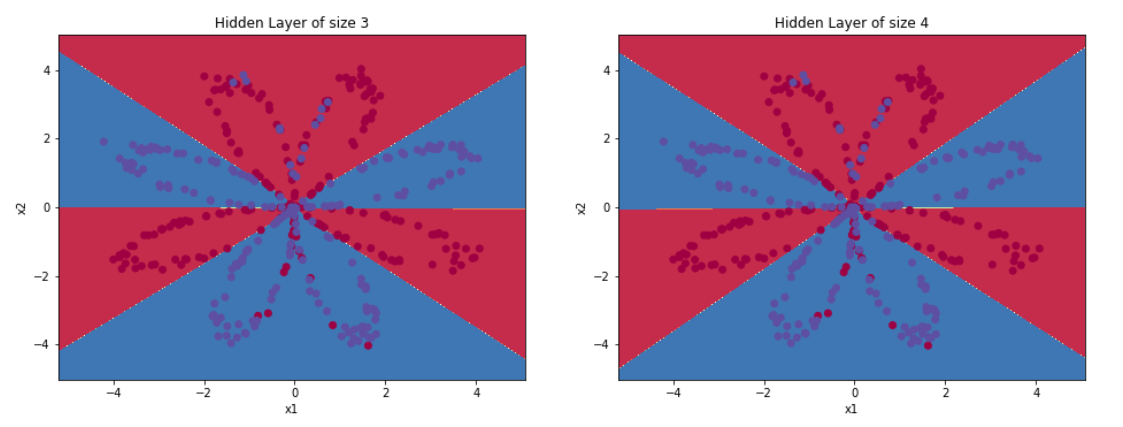
- 可以看到，较大的模型（具有更多隐藏单元）能够更好地适应训练集，直到最终的最大模型过度拟合数据。
- 最好的隐藏层大小似乎在n_h=5附近。实际上，这里的值似乎很适合数据，而且不会引起过度拟合。
- 之后会学习有关正则化的知识，它允许我们使用非常大的模型（如n_h = 50），而不会出现太多过度拟合。
7. 如果改变数据集
# 数据集
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
dataset = "noisy_moons"
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
可以看到该模型也可以很好的拟合新的数据包。
知识点汇总
- 构建神经网络的一般方法是：
- 定义神经网络结构（输入单元的数量，隐藏单元的数量等）
- 初始化模型的参数
- 循环：
- 实施前向传播
- 计算损失
- 实现向后传播
- 更新参数（梯度下降）
- 最后把它们合并到一个nn_model()函数中，当构建好了nn_model（）并学习了正确的参数，就可以预测新的数据。
- 正向传播的过程：
对于 \(x^{(i)}\)（第i个训练样本）而言:
注：\(a^{[2](i)}\) ，其中[2]指第二层，(i)指第i个训练样本。其他符号同理。
\[z^{[1](i)}=w^{[1](i)} x^{(i)} + b^{[1](i)} \tag{1}
\]
\[a^{[1](i)}=tanh(z^{[1](i)}) \tag{2}
\]
\[z^{[2](i)}=w^{[2](i)} a^{[1](i)} + b^{[2](i)} \tag{3}
\]
\[a^{[2](i)}=\sigma(z^{[2](i)}) \tag{4}
\]
向量化实现：
\[Z^{[1]}=W^{[1]} X + b^{[1]} \tag{6}
\]
\[A^{[1] }=tanh(Z^{[1]}) \tag{7}
\]
\[Z^{[2] }=W^{[2] } A^{[1] } + b^{[2] } \tag{8}
\]
\[A^{[2] }=\sigma(Z^{[2]}) \tag{9}
\]
可以按如下方式计算成本J：
\[J=-\frac1m \sum_{i=1}^m \left( y^{(i)} log(a^{[2](i)}) +(1-y^{(i)}) log(1-a^{[2](i)}) \right) \tag{5}
\]
- 因为该题目是一个二分类任务，所以在计算
$A^{[2]}$的时候使用的激活函数是sigma函数，这个函数除了应用在输出层是一个二分类问题的情况下基本不会使用，原因是tanh函数几乎在所有的场合更加优越。 - tanh函数的原型是：
\[a = g^{[1]}(Z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}
\]
\[a '={g^{[1]}}'(Z) = 1-a^2
\]
- 反向传播的过程：
软件包的代码
因为不知道老师提供的软件包中都有什么样的函数，提供哪些功能，让我在理解程序的过程中有些困难，所以把提供的两个软件包的代码放在这：
planar_utils.py中的代码：
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
def plot_decision_boundary(model, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), cmap=plt.cm.Spectral)
def sigmoid(x):
s = 1/(1+np.exp(-x))
return s
def load_planar_dataset():
np.random.seed(1)
m = 400 # number of examples
N = int(m/2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m,D)) # data matrix where each row is a single example
Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2):
ix = range(N*j,N*(j+1))
t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
def load_extra_datasets():
N = 200
noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
no_structure = np.random.rand(N, 2), np.random.rand(N, 2)
return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure
testCases.py中的代码
#-*- coding: UTF-8 -*-
"""
# WANGZHE12
"""
import numpy as np
# 用于测试神经网络结构的数据
def layer_sizes_test_case():
np.random.seed(1)
X_assess = np.random.randn(5, 3)
Y_assess = np.random.randn(2, 3)
return X_assess, Y_assess
# 初始化模型参数的测试数据
def initialize_parameters_test_case():
n_x, n_h, n_y = 2, 4, 1
return n_x, n_h, n_y
# 向前传播的测试数据
def forward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
return X_assess, parameters
# 代价函数的测试数据
def compute_cost_test_case():
np.random.seed(1)
Y_assess = np.random.randn(1, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
a2 = (np.array([[ 0.5002307 , 0.49985831, 0.50023963]]))
return a2, Y_assess, parameters
# 反向传播的测试数据
def backward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
cache = {'A1': np.array([[-0.00616578, 0.0020626 , 0.00349619],
[-0.05225116, 0.02725659, -0.02646251],
[-0.02009721, 0.0036869 , 0.02883756],
[ 0.02152675, -0.01385234, 0.02599885]]),
'A2': np.array([[ 0.5002307 , 0.49985831, 0.50023963]]),
'Z1': np.array([[-0.00616586, 0.0020626 , 0.0034962 ],
[-0.05229879, 0.02726335, -0.02646869],
[-0.02009991, 0.00368692, 0.02884556],
[ 0.02153007, -0.01385322, 0.02600471]]),
'Z2': np.array([[ 0.00092281, -0.00056678, 0.00095853]])}
return parameters, cache, X_assess, Y_assess
# 更新参数的测试数据
def update_parameters_test_case():
parameters = {'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
grads = {'dW1': np.array([[ 0.00023322, -0.00205423],
[ 0.00082222, -0.00700776],
[-0.00031831, 0.0028636 ],
[-0.00092857, 0.00809933]]),
'dW2': np.array([[ -1.75740039e-05, 3.70231337e-03, -1.25683095e-03,
-2.55715317e-03]]),
'db1': np.array([[ 1.05570087e-07],
[ -3.81814487e-06],
[ -1.90155145e-07],
[ 5.46467802e-07]]),
'db2': np.array([[ -1.08923140e-05]])}
return parameters, grads
# 整合成nn_model函数的测试数据
def nn_model_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
return X_assess, Y_assess
# 预测函数的测试数据
def predict_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
return parameters, X_assess
学习感悟
- 不太懂的点：数据的生成；该例子中的Logistic回归的分类的实现；绘制决策边界函数的实现。
