课程1-神经网络和深度学习—第2周-具有神经网络思维的Logistic回归
题目
建立一个逻辑回归分类器来识别猫。这个作业将帮助你了解如何使用神经网络思维方式来做这件事,也将磨练你对深度学习的直觉。
注意:开始之前要下载好所需资料,然后将文件解压到你的代码文件同一级目录下,要确保代码的同一级目录下有lr_utils.py和datasets文件夹。
编程
1 - Packages
在开始之前,我们有需要引入的库:
- numpy :是用Python进行科学计算的基本软件包。
- h5py:是与H5文件中存储的数据集进行交互的常用软件包。
- matplotlib:是一个著名的库,用于在Python中绘制图表。
- lr_utils :在本文的资料包里,这是一个加载资料包里面的数据的简单功能的库。
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
其中 lr_utils.py 代码如下,可以自行打开它查看:
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
解释一下上面的 load_dataset() 返回的值的含义:
- train_set_x_orig :保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
- train_set_y_orig :保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
- test_set_x_orig :保存的是测试集里面的图像数据(本训练集有50张64x64的图像)。
- test_set_y_orig : 保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
- classes : 保存的是以bytes类型保存的两个字符串数据,数据为:classes[0] = b’non-cat’;classes[1] = b’cat’。
2 - Overview of the Problem set
现在我们就要把这些数据加载到主程序里面:
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()
train_set_x_orig.shape, train_set_y.shape, test_set_x_orig.shape, test_set_y.shape
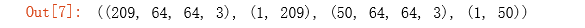
- 可以看到每个图像的shape是(num_px,num_px,3),其中3个通道(RGB)。因此,每个图像都是正方形(height=num_px)和(width=num_px)。
- 之所以在图像数据集(训练和测试)的末尾添加了“_orig”,是因为因为我们要对它们进行预处理。在预处理之后,我们将最终得到train_set_x和test_set_x(标签train_set_y和test_set_y不需要任何预处理)。
- train_set_x_orig和test_set_x_orig的每一行都是一个表示图像的数组。用如下代码可以查看一下训练集里面的图片,可以改变index的值查看一下其他的图片。
index = 50
plt.imshow(train_set_x_orig[index])
#print("train_set_y=" + str(train_set_y)) #看一下训练集里面的标签是什么样的。
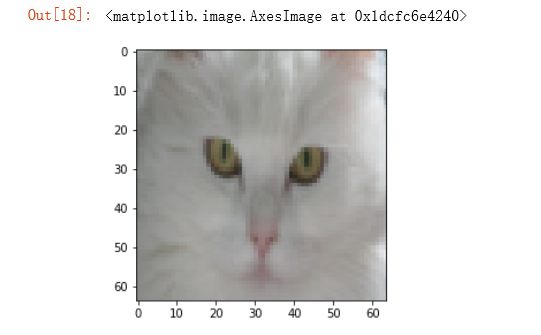
#打印出当前的训练标签值
#使用np.squeeze的目的是压缩维度,【未压缩】train_set_y[:,index]的值为[1] , 【压缩后】np.squeeze(train_set_y[:,index])的值为1
# print("【使用np.squeeze:" + str(np.squeeze(train_set_y[:,index])) + ",不使用np.squeeze: " + str(train_set_y[:,index]) + "】")
# 【使用np.squeeze:1,不使用np.squeeze: [1]】
#只有压缩后的值才能进行解码操作
print("y=" + str(train_set_y[:,index]) + ", it's a " + classes[np.squeeze(train_set_y[:,index])].decode("utf-8") + "' picture")

对以下参数做出解释:
- m_train :训练集里图片的数量。
- m_test :测试集里图片的数量。
- num_px : 训练、测试集里面的图片的宽度和高度(均为64x64)。
train_set_x_orig 是一个维度为(m_train,num_px,num_px,3)的数组。
m_train = train_set_y.shape[1] #训练集里图片的数量。
m_test = test_set_y.shape[1] #测试集里图片的数量。
num_px = train_set_x_orig.shape[1] #训练、测试集里面的图片的宽度和高度(均为64x64)。
#现在看一看我们加载的东西的具体情况
print ("训练集的数量: m_train = " + str(m_train))
print ("测试集的数量 : m_test = " + str(m_test))
print ("每张图片的宽/高 : num_px = " + str(num_px))
print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("训练集_图片的维数 : " + str(train_set_x_orig.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集_图片的维数: " + str(test_set_x_orig.shape))
print ("测试集_标签的维数: " + str(test_set_y.shape))

- 为了方便,要把维度为(64,64,3)的numpy数组重新构造为(64 x 64 x 3,1)的数组,要乘以3的原因是每张图片是由64x64像素构成的,而每个像素点由(R,G,B)三原色构成的,所以要乘以3。
- 在此之后,训练和测试数据集是一个numpy数组,【每列代表一个平坦的图像】 ,应该有m_train和m_test列。
- 当想将形状(a,b,c,d)的矩阵X平铺成形状(b * c * d,a)的矩阵X_flatten时,可以使用以下代码:
# X_flatten = X.reshape(X.shape [0],-1).T #X.T是X的转置
#将训练集的维度降低并转置。
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
#将测试集的维度降低并转置。
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
- 意思是指把数组变为209行的矩阵(因为训练集里有209张图片),但是懒得算列有多少,于是我就用-1告诉程序你帮我算,最后程序算出来时12288列,我再最后用一个T表示转置,这就变成了12288行,209列。
- 测试集亦如此。
- 看看降维之后的情况:
print ("训练集降维最后的维度: " + str(train_set_x_flatten.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集降维之后的维度: " + str(test_set_x_flatten.shape))
print ("测试集_标签的维数 : " + str(test_set_y.shape))

- 为了表示彩色图像,必须为每个像素指定红色,绿色和蓝色通道(RGB),因此像素值实际上是从0到255范围内的三个数字的向量。
- 机器学习中一个常见的预处理步骤是对数据集进行居中和标准化,这意味着可以减去每个示例中整个numpy数组的平均值,然后将每个示例除以整个numpy数组的标准偏差。
- 但对于图片数据集,它更简单,更方便,几乎可以将数据集的每一行除以255(像素通道的最大值),因为在RGB中不存在比255大的数据,所以我们可以放心的除以255,让标准化的数据位于[0,1]之间。
- 现在标准化我们的数据集:
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255
3 - General Architecture of the learning algorithm
- 现在已经把加载的数据弄完了,现在开始构建神经网络来区分猫的图像和非猫的图像。
- 将建立一个逻辑回归,使用神经网络。下图解释了为什么逻辑回归实际上是一个非常简单的神经网络!
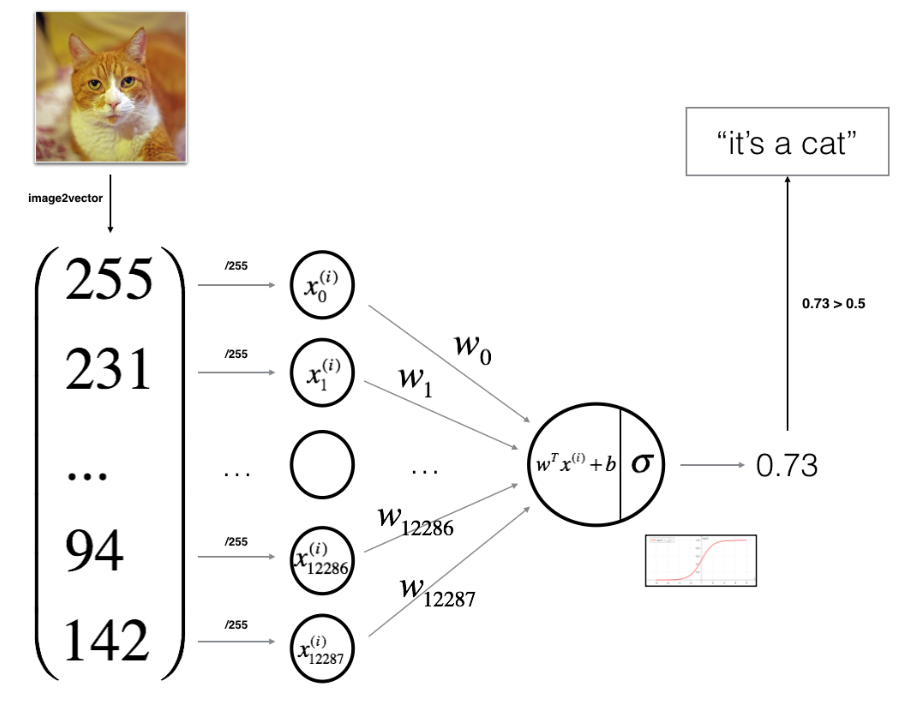
- 算法的数学表达式:
\[z^{(i)}= \omega^Tx^{(i)}+b \tag{1}
\]
\[\hat{y}^{(i)}=a^{(i)}=sigmoid(z^{(i)}) \tag{2}
\]
\[\mathcal{L}(a^{(i)},y^{(i)})=-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)}) \tag{3}
\]
- 然后通过对所有训练样例求和来计算成本:
\[J=\sum_{i=1}^{m}\mathcal{L}(a^{(i)},y^{(i)}) \tag{4}
\]
- 关键步骤——在本练习中,将执行以下步骤:
- 初始化模型的参数
- 通过最小化成本学习模型的参数
- 使用学习到的参数进行预测(在测试集上)
- 分析结果并得出结论
4 - Building the parts of our algorithm
- 建立神经网络的主要步骤是:
- 定义模型结构(例如输入特征的数量)
- 初始化模型的参数
- 循环:
- 计算当前损失(正向传播)
- 计算当前梯度(反向传播)
- 更新参数(梯度下降)
- 使用学习到的参数进行预测(在测试集上)
- 分析结果并得出结论
4.1 - Helper functions
现在构建 \(sigmoid()\) ,需要使用 $ sigmoid(w ^ T x + b)$ 计算来做出预测。
def sigmoid(z):
"""
参数:
z - 任何大小的标量或numpy数组。
返回:
s - sigmoid(z)
"""
s = 1 / (1 + np.exp(-z))
return s
4.2 - Initializing parameters
现在就可以初始化我们需要的参数w和b了。
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w - 维度为(dim,1)的初始化向量。
b - 初始化的标量(对应于偏差)
"""
w = np.zeros(shape = (dim,1))
b = 0
#使用断言来确保我要的数据是正确的
assert(w.shape == (dim, 1)) #w的维度是(dim,1)
assert(isinstance(b, float) or isinstance(b, int)) #b的类型是float或者是int
return (w , b)
4.3 - Forward and Backward propagation
初始化参数的函数已经构建好了,现在就可以执行“前向”和“后向”传播步骤来学习参数。
我们现在要实现一个计算成本函数及其渐变的函数propagate()。
- 逻辑回归的向量化表示
\[Z=[z^{(1)},z^{(2)},\dots,z^{(m)}]=\omega^TX+[b,b,\dots,b]=np.dot(w.T,X) + b \tag{1*m}
\]
\[A=[a^{(1)},a^{(2)},\dots,a^{(m)}]=sigmoid(Z) \tag{1*m}
\]
\[dZ=[dz^{(1)},dz^{(2)},\dots,dz^{(m)}] = A-Y \tag{1*m}
\]
\[d\omega=\frac1mXdZ^T=(1 / m) * np.dot(X, (A - Y).T) \tag{n*1}
\]
\[db=\frac1m\sum_{i=1}^mdz^{(i)}=(1 / m) * np.sum(A - Y) \tag{R}
\]
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 矩阵类型为(num_px * num_px * 3,训练数量)
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost- 逻辑回归的负对数似然成本
dw - 相对于w的损失梯度,因此与w相同的形状
db - 相对于b的损失梯度,因此与b的形状相同
"""
m = X.shape[1]
#正向传播
A = sigmoid(np.dot(w.T,X) + b) #计算激活值,请参考公式2。
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) #计算成本,请参考公式3和4。
#反向传播
dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。
#使用断言确保数据是正确的
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
#创建一个字典,把dw和db保存起来。
grads = {
"dw": dw,
"db": db
}
return (grads , cost)
4.4 - Optimization
- 现在要使用梯度下降更新参数。
- 目标是通过最小化成本函数 \(J\)来学习 \(\omega\)
和\(b\)。对于参数 \(\theta\),更新规则是 $ \theta = \theta - \alpha \text{ } d\theta\(,其中\)\alpha$是学习率。
def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations - 优化循环的迭代次数
learning_rate - 梯度下降更新规则的学习率
print_cost - 每100步打印一次损失值
返回:
params - 包含权重w和偏差b的字典
grads - 包含权重和偏差相对于成本函数的梯度的字典
costs - 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
#记录成本
if i % 100 == 0:
costs.append(cost) #append()函数用于在列表末尾添加新的对象。
#打印成本数据
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
params = {
"w" : w,
"b" : b }
grads = {
"dw": dw,
"db": db }
return (params , grads , costs)
4.5 - Predict
- 上一步中的optimize函数会输出已学习的w和b的值,我们可以使用w和b来预测数据集X的标签。
- 现在我们要实现预测函数predict()。计算预测有两个步骤:
- \(\hat{Y}=A=\sigma( \omega^TX+b)\)
- 将a的值变为0(如果激活值<= 0.5)或者为1(如果激活值> 0.5)
- 然后将预测值存储在向量Y_prediction中。
def predict(w , b , X ):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
m = X.shape[1] #图片的数量
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0],1)
#计预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T , X) + b)
for i in range(A.shape[1]):
#将概率 a [0,i]转换为实际预测 p [0,i]
Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
#使用断言
assert(Y_prediction.shape == (1,m))
return Y_prediction
5 - Merge all functions into a model
- 现在要把这些函数统统整合到一个model()函数中,届时只需要调用一个model()就基本上完成所有的事了。
- 实现模型功能。使用以下符号:
- Y_prediction_test:在测试集上的预测
- Y_prediction_train:在训练集上的预测
- w, costs, grads:optimize()函数的输出
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w , b = initialize_with_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train , num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
#abs()函数用于返回数字的绝对值
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
把整个model构建好之后我们这就算是正式的实际测试了,来实际跑一下。
print("====================测试model====================")
#这里加载的是真实的数据,请参见上面的代码部分。
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

如果更改一下学习率和迭代次数,有可能会发现训练集的准确性可能会提高,但是测试集准确性会下降,这是由于过拟合造成的,但是并不需要担心,以后会使用更好的算法来解决这些问题的。
- 使用下面的代码(并更改索引变量),您可以查看测试集图片上的预测。
- 这里的classes的类型是dtype=’|S7’ ,取值的时候,需要用int强转一下,否则报错。(不太懂)
index = 32
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[int(d["Y_prediction_test"][0,index])].decode("utf-8") + "\" picture.")

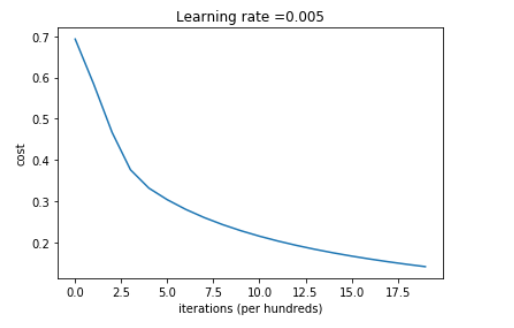
- 可以在后面加一点东西,绘制成本函数和梯度的图像。可以看到成本下降,它显示参数正在被学习:
#绘制图
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
6 - Further analysis (optional/ungraded exercise)
- 进一步分析一下,并研究学习率alpha的可能选择。为了让渐变下降起作用,我们必须明智地选择学习速率。
- 学习率\(\alpha\)决定了我们更新参数的速度。如果学习率过高,我们可能会“超过”最优值。同样,如果它太小,我们将需要太多迭代才能收敛到最佳值。这就是为什么使用良好调整的学习率至关重要的原因。
- 可以比较一下模型的学习曲线和几种学习速率的选择。也可以尝试使用不同于我们初始化的learning_rates变量包含的三个值,看一下会发生什么。
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
#设置图例
#图例legen()函数,参数loc图例所有figure位置;参数shadow控制是否在图例后面画一个阴影
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90') #设置图例legend背景
plt.show()
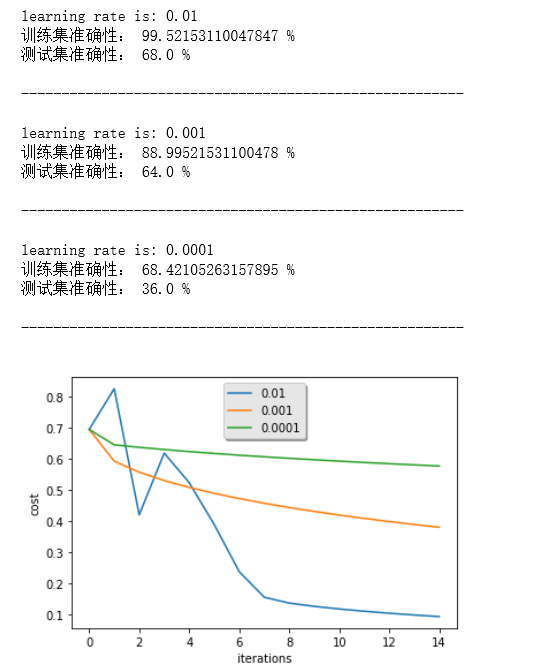
- 不同的学习率会产生不同的成本,从而产生不同的预测结果。
- 如果学习率太大(0.01),则成本可能上下波动。它甚至可能会发散(尽管在本例中,使用0.01最终还是会得到很好的成本值)。
- 低成本并不意味着更好的模式。你得检查一下是否有过拟合的可能。当训练精度远高于测试精度时就会发生这种情况。
- 在深入学习中,我们通常建议您:
- 选择可以更好地最小化成本函数的学习率。
- 如果您的模型过拟合,请使用其他技术来减少过拟合。(我们将在以后的视频中讨论这个问题。)
知识点整理
- 预处理新数据集的常见步骤:
- 找出问题的尺寸和形状(m_-train,m_-test,num_-px,…)
- 重新调整数据集的形状,使每个示例现在都是一个大小向量(num-pxnum-px3,1)
- “标准化”数据
- 算法的数学表达式:
\[z^{(i)}= \omega^Tx^{(i)}+b \tag{1}
\]
\[\hat{y}^{(i)}=a^{(i)}=sigmoid(z^{(i)}) \tag{2}
\]
\[\mathcal{L}(a^{(i)},y^{(i)})=-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)}) \tag{3}
\]
- 然后通过对所有训练样例求和来计算成本:
\[J=\sum_{i=1}^{m}\mathcal{L}(a^{(i)},y^{(i)}) \tag{4}
\]
- 逻辑回归的向量化表示
\[Z=[z^{(1)},z^{(2)},\dots,z^{(m)}]=\omega^TX+[b,b,\dots,b]=np.dot(w.T,X) + b \tag{1*m}
\]
\[A=[a^{(1)},a^{(2)},\dots,a^{(m)}]=sigmoid(Z) \tag{1*m}
\]
\[dZ=[dz^{(1)},dz^{(2)},\dots,dz^{(m)}] = A-Y \tag{1*m}
\]
\[d\omega=\frac1mXdZ^T=(1 / m) * np.dot(X, (A - Y).T) \tag{n*1}
\]
\[db=\frac1m\sum_{i=1}^mdz^{(i)}=(1 / m) * np.sum(A - Y) \tag{R}
\]
- 建立神经网络的主要步骤是:
- 定义模型结构(例如输入特征的数量)
- 初始化模型的参数
- 循环:
- 计算当前损失(正向传播)
- 计算当前梯度(反向传播)
- 更新参数(梯度下降)
- 使用学习到的参数进行预测(在测试集上)
- 分析结果并得出结论
遇到的问题
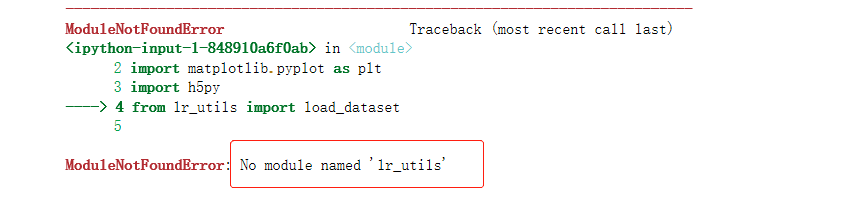
- 吴恩达的《深度学习》作业包解压缩之后需要将lr_utils.py文件导入当前的编译环境。
- lr_utils不是库而是一个文件。它不需要安装,只需要导入到当前编译器就行。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号