神经网络BP算法推导
Cost Function
-
\(L\):表示神经网络的总层数。
-
\(S_l\):表示第\(l\)层的单元数(即神经元的数量),其中不包括第\(l\)层的偏置单元。
-
\(K\):输出层单元数目。
-
\(\left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k\):表示输出神经网络输出向量中的第\(k\)个元素。
-
如果一个网络在第\(j\)层有\(S_j\)个单元,在\(j+1\)层有\(S_{j+1}\)个单元,那么矩阵\(\theta^{\left(j\right)}\),即控制第\(j\)层到第\(j+1\)层映射的矩阵,他的维度是\(S_{j+1}\times(S_j+1)\).
-
神经网络代价函数(带正则化项):
\[J(\theta)=\frac1m \sum_{i=1}^m \sum_{k=1}^K \left[ - y^{\left(i \right)}_k log \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k - \left( 1-y^{\left( i\right)}_k \right) log \left( 1- \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k \right) \right] + \frac {\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_l} \sum_{j=1}^{S_{l+1}} \left( \Theta_{ji}^ { \left( l \right) } \right)^2
\]
- 看起来复杂很多的代价函数背后的思想还是一样的,通过代价函数来观察算法预测的结果与真实情况的误差有多大。
- 唯一不同的是对于每一行特征,都会给出\(K\)个预测。在\(K\)个预测中选择可能性最高的一个,将其与\(y\)中的实际数据进行比较。
- 正则化的那一项是排除了每层的\(\theta_0\)后,每一层的\(\theta\)矩阵的和。最里面的循环\(j\)循环所有的行,由\(S_{l+1}\)层的激活单元数决定;循环\(i\)则循环所有的列,由\(S_l\)层的激活单元数决定。
Forward propagation
假设有一个三层的神经网络
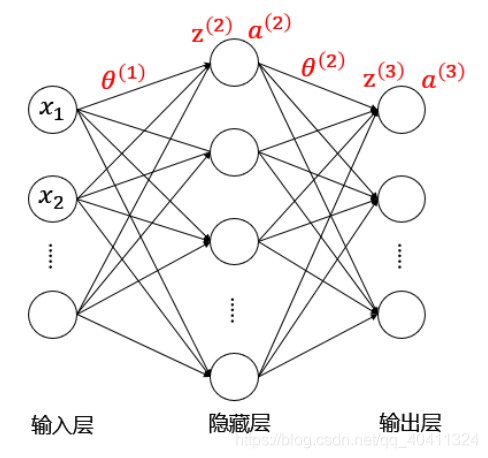
参数含义:
- \(\theta^{\left(i\right)}\):第\(i\)层的参数矩阵(即控制第\(i\)层到第\(i+1\)层映射的矩阵)
- \(z^{\left(l\right)}\):第\(l\)层的输入
- \(a^{\left(l\right)}\):第\(l\)层的输出
向前传播算法过程:(其中\(g\)为sigmoid激活函数。)
- \(a^{\left(1\right)}=x \quad (add \quad a_0^{\left(1\right)})\)
- \(z^{\left(2\right)}=\theta^{\left(1\right)}a^{\left(1\right)}\)
- \(a^{\left(2\right)}=g\left(z^{\left(2\right)}\right) \quad (add \quad a_0^{\left(2\right)})\)
- \(z^{\left(3\right)}=\theta^{\left(2\right)}a^{\left(2\right)}\)
- \(a^{\left(3\right)}=g\left(z^{\left(3\right)}\right)=h_\theta(x)\)
Backpropagation Algorithm
参数含义:
- \(\delta^{\left(l\right)}\):第\(l\)层的误差
- \(y\):每个样本的标签(要转化成非线性相关的向量)
- \(h\):每个样本的预测值
先来从后往前计算每层的“误差“。注意到这里的误差用双引号括起来,因为并不是真正的误差。
- \(\delta^{\left(3\right)}=h-y=a^{\left(3\right)}-y\)
- \(\delta^{\left(2\right)}=\left(\theta^{\left(2\right)}\right)^T·\delta^{\left(3\right)}.*{g^\prime (z^{\left(2\right)}) }\)
- 没有\(\delta^{\left(1\right)}\),因为第一层是输入变量不存在误差。
然后来计算每层参数矩阵的梯度,用\(\Delta^{(l)}\)表示。
当\(\lambda=0\)时,即不考虑正则化处理
- \(\Delta^{(2)}=a^{\left(2\right)}·\delta^{\left(3\right)}\)
- \(\Delta^{(1)}=a^{\left(1\right)}·\delta^{\left(2\right)}\)
则利用反向传播算法计算所有的偏导数(不考虑正则化)
- \(\frac{\partial}{\partial \Theta^{\left( 2 \right)}} J\left(\Theta \right) = \Delta^{\left( 2 \right)}=a^{\left(2\right)}·\delta^{\left(3\right)}\)
- \(\frac{\partial}{\partial \Theta^{\left( 1 \right)}} J\left(\Theta \right) = \Delta^{\left( 1 \right)}=a^{\left(1\right)}·\delta^{\left(2\right)}\)
推导:
- 要优化的参数有\(\theta^{\left( 2 \right)}\)、\(\theta^{\left( 1 \right)}\)。
- 利用梯度下降法的思想,我们只需要求解出代价函数对参数的梯度即可。
- 假设只有一个输入样本,则代价函数是:
\[J\left(\theta \right)=-y \log h(x)-(1-y)\log (1-h(x))
\]
- 回顾下正向传递的过程,理解其中函数的嵌套关系:
- \(a^{\left(1\right)}=x \quad (add \quad a_0^{\left(1\right)})\)
- \(z^{\left(2\right)}=\theta^{\left(1\right)}a^{\left(1\right)}\)
- \(a^{\left(2\right)}=g\left(z^{\left(2\right)}\right) \quad (add \quad a_0^{\left(2\right)})\)
- \(z^{\left(3\right)}=\theta^{\left(2\right)}a^{\left(2\right)}\)
- \(a^{\left(3\right)}=g\left(z^{\left(3\right)}\right)=h_\theta(x)\)
- 然后我们来求解代价函数对参数的梯度:\(\frac{\partial}{\partial \theta^{\left( 2 \right)}} J\left(\theta \right)\),\(\frac{\partial}{\partial \theta^{\left( 1 \right)}} J\left(\theta \right)\)
- 根据链式求导法则,可以计算得到:
\[\frac{\partial}{\partial \theta^{\left( 2 \right)}} J\left(\theta \right)=\frac{\partial J\left(\theta \right)}{\partial a^{\left( 3 \right)}}·\frac{\partial a^{\left( 3 \right)}}{\partial z^{\left( 3 \right)}}·\frac {\partial z^{\left( 3 \right)}}{\partial \theta^{\left( 2 \right)}}
\]
- 其中,$\frac{\partial J\left(\theta \right)}{\partial a^{\left( 3 \right)}}=\frac{\partial J\left(\theta \right)}{\partial h(x)}=-\frac yh+(1-y)\frac1{1-h}=\frac{h-y}{h·(1-h)}$
- $\frac{\partial a^{\left( 3 \right)}}{\partial z^{\left( 3 \right)}}=\frac{ e^{-z} }{ (1+e^-z)^2}=a^{\left( 3 \right)}·\left(1-a^{\left( 3 \right)}\right)=h·(1-h)$
- $\frac {\partial z^{\left( 3 \right)}} {\partial \theta^{\left( 2 \right)}}=a^{(2)}$
- 所以可得:
\[\frac{\partial}{\partial \theta^{\left( 2 \right)}} J\left(\theta \right)=(h-y)·a^{(2)}=\delta^{\left(3\right)}·a^{(2)}
\]
- 同理,根据链式求导法则,计算:
\[\frac{\partial}{\partial \theta^{\left( 1 \right)}} J\left(\theta \right)=\frac{\partial J\left(\theta \right)}{\partial a^{\left( 3 \right)}}·\frac{\partial a^{\left( 3 \right)}}{\partial z^{\left( 3 \right)}}·\frac {\partial z^{\left( 3 \right)}}{\partial a^{\left( 2 \right)}}·\frac{\partial a^{\left( 2 \right)}}{\partial z^{\left( 2 \right)}}·\frac {\partial z^{\left( 2 \right)}}{\partial \theta^{\left( 1 \right)}}
\]
- 其中,由上可知,$\frac{\partial J\left(\theta \right)}{\partial a^{\left( 3 \right)}}·\frac{\partial a^{\left( 3 \right)}}{\partial z^{\left( 3 \right)}}=h-y=\delta^{\left(3\right)}$
- $\frac {\partial z^{\left( 3 \right)}}{\partial a^{\left( 2 \right)}}=\theta^{(2)}$
- $\frac{\partial a^{\left( 2 \right)}}{\partial z^{\left( 2 \right)}}=g^\prime\left(z^{\left(2\right)}\right)$
- $\frac {\partial z^{\left( 2 \right)}}{\partial \theta^{\left( 1 \right)}}=a^{(1)}$
- 所以可得:
\[\frac{\partial}{\partial \theta^{\left( 1 \right)}} J\left(\theta \right)=\delta^{\left(3\right)} \theta^{(2)} g^\prime\left(z^{\left(2\right)}\right) a^{(1)}=\delta^{\left(2\right)}·a^{(1)}
\]
当\(\lambda \neq 0\)时,即考虑正则化处理:
\[\frac{\partial}{\partial \Theta_{ij}^{\left( l \right)}} J\left(\Theta \right) = D_{ij}^{\left( l \right)}= \frac1m \Delta_{ij}^{\left( l \right)} \quad for \quad j=0
\]
\[\frac{\partial}{\partial \Theta_{ij}^{\left( l \right)}} J\left(\Theta \right) = D_{ij}^{\left( l \right)}= \frac1m \Delta_{ij}^{\left( l \right)}+\frac{\lambda}{m} \Theta_{ij}^{\left( l \right)} \quad for \quad j \geq 1
\]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号