编程作业4.1：神经网络反向传播（BP算法）

题目

• 在本练习中将实现神经网络的反向传播算法，并将其应用于手写数字识别任务。
• 在之前的练习中，已经实现了神经网络的前馈传播，并使用Andrew Ng提供的权值来预测手写数字。
• 在本练习中，将自己实现反向传播算法来学习神经网络的参数。本次的数据与上次作业是一样的，这里不再赘述。

编程实现

1.Neural Networks 神经网络

1.1 Visualizing the data

• 随机选取100个样本并可视化。
• 训练集共有5000个训练样本，每个样本是20*20像素的数字的灰度图像，每个像素代表一个浮点数，表示该位置的灰度强度。
• 20×20的像素网格被展开成一个400维的向量。在我们的数据矩阵X中，每一个样本都变成了一行，这给了我们一个5000×400矩阵X，每一行都是一个手写数字图像的训练样本。

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
import scipy.optimize as opt
from sklearn.metrics import classification_report  # 这个包是评价报告

def load_mat(path):
    '''读取数据'''
    data = loadmat(path)  # return a dict
    X = data['X']
    y = data['y'].flatten() # 这里消除了一个维度，方便后面的计算 （5000，）
    
    return X, y  

#定义可视化函数
def plot_100_images(X):
    """随机画100个数字"""
    index = np.random.choice(range(5000), 100) # 随机选100个样本
    images = X[index]
    fig, ax_array = plt.subplots(10, 10, sharey=True, sharex=True, figsize=(8, 8))
    for r in range(10):
        for c in range(10):
            ax_array[r, c].matshow(images[r*10 + c].reshape(20,20), cmap='gray_r')
    plt.xticks([])
    plt.yticks([])
    plt.show()

    
X,y = load_mat('D:\BaiduNetdiskDownload\data_sets\ex4data1.mat')
plot_100_images(X)

1.2 Model representation 模型表示

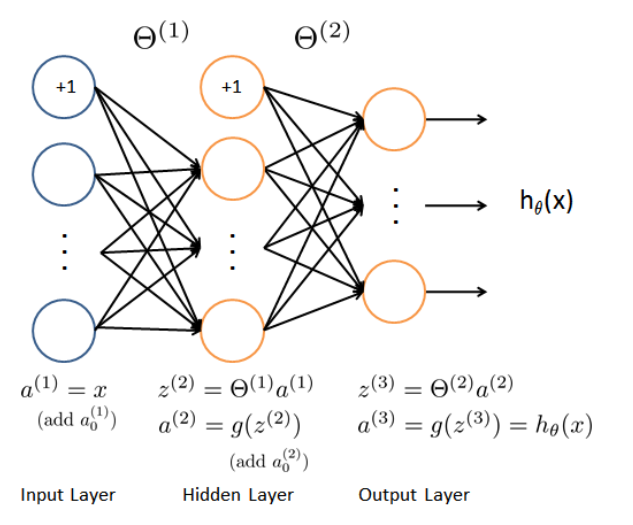
• 我们的网络有三层，输入层，隐藏层，输出层。
• 我们的输入是数字图像的像素值（即训练集特征的数量），因为每个数字的图像大小为20*20，所以我们输入层有400个单元（这里不包括偏置单元）。

1.2.1 load train data set 读取数据

• 首先我们要将标签值（1，2，3，4，…，10）转化成非线性相关的向量，向量对应位置（y[i-1]）上的值等于1，例如y[0]=6转化为y[0]=[0,0,0,0,0,1,0,0,0,0]。

from sklearn.preprocessing import OneHotEncoder 
# 在 sklearn 包中，OneHotEncoder 函数非常实用，它可以实现将分类特征的每个元素转化为一个可以用来计算的值。

def expand_y(y):
    result = []
    # 把y中每个类别转化为一个向量，对应的lable值在向量对应位置上置为1
    for i in y:
        y_array = np.zeros(10)
        y_array[i-1] = 1
        result.append(y_array) # 给result的列表尾部追加元素
    '''
    # 或者用sklearn中OneHotEncoder函数
    encoder =  OneHotEncoder(sparse=False)  # return a array instead of matrix
    y_onehot = encoder.fit_transform(y.reshape(-1,1))
    return y_onehot
    ''' 
    return np.array(result) # 将数据转化为矩阵

• 获取训练数据集，以及对训练集做相应的处理，得到我们的input X，lables y。

raw_X, raw_y = load_mat('D:\BaiduNetdiskDownload\data_sets\ex4data1.mat')

X = np.insert(raw_X, 0, 1, axis=1) # 为X添加了一列常数项 1，(5000, 401)
y = expand_y(raw_y)

X.shape, y.shape

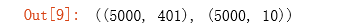
1.2.2 load weight 读取权重

• 提供了已经训练好的参数\(\theta_1\)，\(\theta_2\)，存储在ex4weight.mat文件中。
• 这些参数的维度由神经网络的大小决定，第二层有25个单元，输出层有10个单元(对应10个数字类)。

def load_weight(path):
    data = loadmat(path)
    return data['Theta1'], data['Theta2'] 


t1, t2 = load_weight('D:\BaiduNetdiskDownload\data_sets\ex4weights.mat')
t1.shape, t2.shape

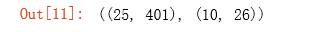
1.2.3 展开参数

• 这里需要提前将参数展开为一维的向量，因为在后面采用fmin_ncg函数训练参数时需要将theta的初始值赋予函数，这里的初始值要求是一维向量，因此在后面代价函数和梯度函数的定义中也要注意返回一维的梯度。

# 参数从矩阵形式展开成一维向量
def serialize(a, b):
    '''展开参数'''
    return np.r_[a.flatten(),b.flatten()] # np.r_：是按列连接两个矩阵

theta = serialize(t1, t2)  # 展开参数，25*401+10*26=10285
theta.shape  # (10285,)

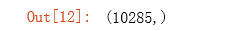
# 参数从向量形式还原成矩阵
def deserialize(seq):
    '''提取参数'''
    return seq[:25*401].reshape(25, 401), seq[25*401:].reshape(10, 26)

1.3 Feedforward and cost function 前馈和代价函数

1.3.1 Feedforward

• 确保每层的单元数，注意输出时加一个偏置单元，s(1)=400+1，s(2)=25+1，s(3)=10。

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def feed_forward(theta, X,):
    '''得到每层的输入和输出'''
    t1, t2 = deserialize(theta) # 参数从向量形式还原成矩阵
    # t1, t2已经插入过偏置单元，这里就不用插入了
    a1 = X
    z2 = a1 @ t1.T
    a2 = np.insert(sigmoid(z2), 0, 1, axis=1)
    z3 = a2 @ t2.T
    a3 = sigmoid(z3)
    
    return a1, z2, a2, z3, a3 

a1, z2, a2, z3, h = feed_forward(theta, X)

1.3.2 Cost function

• 神经网络的代价函数（不带正则化项）:

\[J(\theta)=\frac1m \sum_{i=1}^m \sum_{k=1}^K \left( - y^{\left(i \right)}_k log \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k - \left( 1-y^{\left( i\right)}_k \right) log \left( 1- \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k \right) \right) \]

• 输出层输出的是对样本的预测，包含5000个数据，每个数据对应了一个包含10个元素的向量，代表了结果有10类。在公式中，每个元素与log项对应相乘。
• 最后我们使用提供训练好的参数θ，算出的cost应该为0.287629

def cost(theta, X, y):
    a1, z2, a2, z3, h = feed_forward(theta, X)
    J = 0
    # use verctorization
    J = - y * np.log(h) - (1 - y) * np.log(1 - h)
    return J.sum() / len(X)

cost(theta, X, y)  

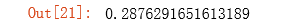
1.4.Regularized cost function 正则化代价函数

• 神经网络的代价函数（带正则化项）:

\[J(\theta)=\frac1m \sum_{i=1}^m \sum_{k=1}^K \left[ - y^{\left(i \right)}_k log \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k - \left( 1-y^{\left( i\right)}_k \right) log \left( 1- \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k \right) \right] + \frac {\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_l} \sum_{j=1}^{S_{l+1}} \left( \Theta_{ji}^ { \left( l \right) } \right)^2 \]

• 此题中把正则化具体化为：注意每层的偏置项不进行正则化

\[J(\theta)=\frac1m \sum_{i=1}^m \sum_{k=1}^K \left[ - y^{\left(i \right)}_k log \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k - \left( 1-y^{\left( i\right)}_k \right) log \left( 1- \left( h_\Theta \left( x^{\left( i\right)} \right) \right)_k \right) \right] + \frac {\lambda}{2m} \left[ \sum_{i=1}^{400} \sum_{j=1}^{25} \left( \Theta_{ji}^ { \left( 1 \right) } \right)^2 + \sum_{i=1}^{25} \sum_{j=1}^{10} \left( \Theta_{ji}^ { \left( 2 \right) } \right)^2 \right] \]

def regularized_cost(theta, X, y, l=1):
    '''正则化时忽略每层的偏置项，也就是参数矩阵的第一列'''
    t1, t2 = deserialize(theta)
    reg = np.sum(t1[:,1:] ** 2) + np.sum(t2[:,1:] ** 2)  # or use np.power(a, 2)
    return l / (2 * len(X)) * reg + cost(theta, X, y)


regularized_cost(theta, X, y, 1)  

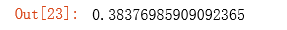
2.Backpropagation 反向传播

2.1 Sigmoid gradient S函数的导数

\[g^\prime (z) = g(z)\left(1-g\left(z\right)\right) \]

def sigmoid_gradient(z):
    return sigmoid(z) * (1 - sigmoid(z))

2.2 Random initialization 随机初始化

• 为解决对称权重问题，以防止对同一神经元的所有参数/权重都相等，需要随机地对初始的参数/权重赋值。
• 一个有效的策略是在均匀分布(−e，e)中随机选择值，我们可以选择 e = 0.12 这个范围的值来确保参数足够小，使得训练更有效率。

def random_init(size):
    '''从服从的均匀分布的范围中随机返回size大小的值'''
    return np.random.uniform(-0.12, 0.12, size)

2.3 Backpropagation 反向传播

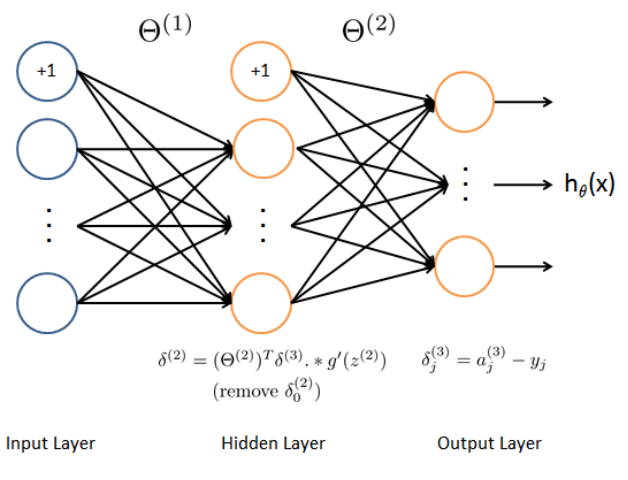
• 目标：获取整个网络代价函数的梯度。以便在优化算法中求解。
• 一定要理解正向传播和反向传播的过程，才能弄清楚各种参数在网络中的维度。

print('a1', a1.shape,'t1', t1.shape)
print('z2', z2.shape)
print('a2', a2.shape, 't2', t2.shape)
print('z3', z3.shape)
print('a3', h.shape)

# 利用反向传播算法计算所有的偏导数（不考虑正则化）
def gradient(theta, X, y):
    '''
    unregularized gradient, notice no d1 since the input layer has no error 
    return 所有参数theta的梯度，故梯度D(i)和参数theta(i)同shape，重要。
    '''
    t1, t2 = deserialize(theta)
    a1, z2, a2, z3, h = feed_forward(theta, X)
    d3 = h - y # (5000, 10)
    d2 = d3 @ t2[:,1:] * sigmoid_gradient(z2)  # (5000, 25)
    D2 = d3.T @ a2  # (10, 26)
    D1 = d2.T @ a1 # (25, 401)
    D = (1 / len(X)) * serialize(D1, D2)  # (10285,)
    
    return D

2.4 Regularized Neural Networks 正则化神经网络

\[\frac{\partial}{\partial \Theta_{ij}^{\left( l \right)}} J\left(\Theta \right) = D_{ij}^{\left( l \right)}= \frac1m \Delta_{ij}^{\left( l \right)} \quad for \quad j=0 \]

\[\frac{\partial}{\partial \Theta_{ij}^{\left( l \right)}} J\left(\Theta \right) = D_{ij}^{\left( l \right)}= \frac1m \Delta_{ij}^{\left( l \right)}+\frac{\lambda}{m} \Theta_{ij}^{\left( l \right)} \quad for \quad j \geq 1 \]

# 利用反向传播算法计算所有的偏导数（考虑正则化）
def regularized_gradient(theta, X, y, l=1):
    """不惩罚偏置单元的参数"""
    t1, t2 = deserialize(theta)
    a1, z2, a2, z3, h = feed_forward(theta, X)
    D1, D2 = deserialize(gradient(theta, X, y))
    t1[:,0] = 0 #就是取所有行的第0个数据，即赋第一列的值为0
    t2[:,0] = 0
    reg_D1 = D1 + (l / len(X)) * t1
    reg_D2 = D2 + (l / len(X)) * t2
    
    return serialize(reg_D1, reg_D2)

2.5 Gradient checking 梯度检测

• 目的是保证在反向传播中没有错误，采取一种叫做梯度的数值检验（Numerical Gradient checking）
• 这种方法的思想是通过估计梯度值来检验我们计算的导数是否真的是我们要求的。
• 首先计算反向传播中的梯度向量。
• 再采用双侧差分法，即在某点领域取一个很小的值，利用左右两点的连线来作为该点斜率的逼近\(\frac{d}{d\theta}J(\theta) \approx \frac{J(\theta +\epsilon)-J(\theta -\epsilon)}{2\epsilon}\)，\(\epsilon\)一般取\(10^{-4}\)。
• 当\(\theta\)是一个向量时，可以使其他$ \theta_j\(保持不变，对每个\) \theta_i$分别进行双侧差分，而后得到数值上的梯度向量。
• 最后将神经网络代价函数中所有参数的数值梯度向量与在反向传播中得到的梯度进行比较，看是否十分接近，这样能保证在进行反向传播时所计算的梯度是正确的。检查完之后禁用梯度检验函数以保证BP算法运行的空间节约训练时间。

def gradient_checking(theta, X, y, e):
    def a_numeric_grad(plus, minus):
        """
        对每个参数theta_i计算数值梯度，即理论梯度。
        """
        return (regularized_cost(plus, X, y) - regularized_cost(minus, X, y)) / (e * 2)
   
    numeric_grad = [] 
    for i in range(len(theta)):
        plus = theta.copy()  # deep copy otherwise you will change the raw theta
        minus = theta.copy()
        plus[i] = plus[i] + e
        minus[i] = minus[i] - e
        grad_i = a_numeric_grad(plus, minus)
        numeric_grad.append(grad_i) # append() 追加单个元素到List的尾部，只接受一个参数，参数可以是任何数据类型，被追加的元素在List中保持着原结构类型。
    
    numeric_grad = np.array(numeric_grad) # 转化为矩阵形式
    analytic_grad = regularized_gradient(theta, X, y) 
    #  np.linalg.norm 表示求取向量的范数
    diff = np.linalg.norm(numeric_grad - analytic_grad) / np.linalg.norm(numeric_grad + analytic_grad)

    print('If your backpropagation implementation is correct,\nthe relative difference will be smaller than 10e-9 (assume epsilon=0.0001).\nRelative Difference: {}\n'.format(diff))

gradient_checking(theta, X, y, epsilon= 0.0001)

2.6 Learning parameters using fmincg 优化参数

def nn_training(X, y):
    init_theta = random_init(10285)  # 随机初始化参数：25*401 + 10*26

    # minimize是局部最优的解法
    # fun: 求最小值的目标函数
    # x0：变量的初始猜测值，如果有多个变量，需要给每个变量一个初始猜测值
    # args：是传递给优化函数的参数
    # method:求极值的方法
    # jac：计算梯度向量的方法
    # options：A dictionary of solver options. 
    res = opt.minimize(fun=regularized_cost,
                       x0=init_theta,
                       args=(X, y, 1),
                       method='TNC',
                       jac=regularized_gradient,
                       options={'maxiter': 400})
    return res

res = nn_training(X, y)
res

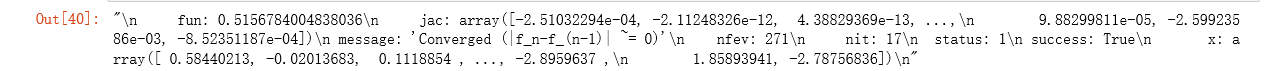
def accuracy(theta, X, y):
    _, _, _, _, h = feed_forward(res.x, X)
    y_pred = np.argmax(h, axis=1) + 1 #axis=1，其中1代表行，表示返回每行最大值的索引。
    #sklearn中的classification_report函数用于显示主要分类指标的文本报告．在报告中显示每个类的精确度，召回率，F1值等信息
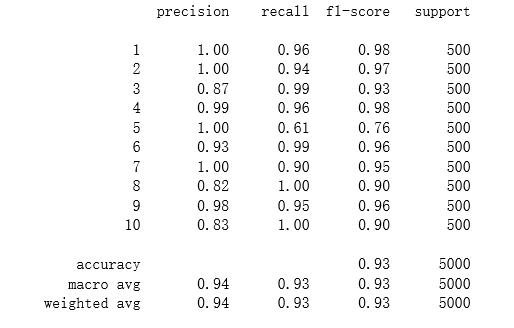
    print(classification_report(y, y_pred))
    
accuracy(res.x, X, raw_y)

#列表左边的一列为分类的标签名（代表分类有十类）
#右边support列为每个标签的出现次数
#avg / total行为各列的均值（support列为总和）
#precision recall f1-score三列分别为各个类别的精确度/召回率及F1值

3.Visualizing the hidden layer 可视化隐藏层

• 理解神经网络是如何学习的一个很好的办法是，可视化隐藏层单元所捕获的内容。
• 通俗的说，给定一个的隐藏层单元，可视化它所计算的内容的方法是找到一个输入x，x可以激活这个单元（也就是说有一个激活值 \(a^{(l)}_i\) 接近与1）。
• 对于我们所训练的网络，注意到\(\theta^{\left(1\right)}\)中每一行都是一个401维的向量，代表每个隐藏层单元的参数。如果我们忽略偏置项，我们就能得到400维的向量，这个向量代表每个样本输入到每个隐层单元的像素的权重。
• 因此可视化的一个方法是，reshape这个400维的向量为（20，20）的图像然后输出。
• 因为权重中每个值代表了对应输入神经元的权重，在这里就是一个数字的某个像素对下一层的影响有多大，如果某些像素值就是特别关键的可以识别出这个输入x是数字几的时候，那它们对应的权重自然就大，因此可以把隐层中的权重可视化可以看出隐层在尝试识别出一些笔画或者重要的图案。

# 定义可视化隐藏层的函数 
def plot_hidden(theta):
    t1, _ = deserialize(theta) # 取theta1,25*401
    t1 = t1[:, 1:] # 忽略偏置项。得到25*400的矩阵
    
    # 表示子图网格(grid)的行数与列数为5行5列
    # sharex=True, sharey=True,x或y轴属性将在所有子图(subplots)中共享
    fig,ax_array = plt.subplots(5, 5, sharex=True, sharey=True, figsize=(6,6))
    for r in range(5):
        for c in range(5):
            # matshow函数可使矩阵可视化；将theta1中的每一行都转化为一个20*20的矩阵然后可视化
            ax_array[r, c].matshow(t1[r * 5 + c].reshape(20, 20), cmap='gray_r')
            plt.xticks([]) # 去除刻度，美观
            plt.yticks([])
    plt.show()
    
plot_hidden(res.x)

总结

• BP算法究竟是在干什么：我们的目标是最小化代价函数，也就是训练权重得到最小的代价函数，为了得到这个权重我们需要计算代价函数\(J(\theta)\)以及他对权重的梯度（偏导数）$ \frac{\partial}{\partial \theta_{ji}^{\left(l \right) }} J(\theta)$，然后再把这两个值传给最优化函数minimize就可以得到训练好的权重了，也就是最小化了代价函数了。
• 关于BP算法的推导，在学吴恩达机器学习视频的神经网络那节时，给出了许多公式，比如计算每层的误差，每层参数的梯度，但并没有给出推导过程。为了更好的理解，写了简单的推导了过程，这里只弄懂了未正则化的神经网络——神经网络BP算法推导
• 训练神经网络的步骤
  • 参数随机初始化
  • 利用正向传播算法计算所有的\(h_\theta(x)\)
  • 编写计算代价函数\(J(\theta)\)的代码
  • 利用反向传播计算所有的偏导数
  • 利用数值检验方法检验这些偏导数
  • 利用优化算法来最小化代价函数

参考资料

神经网络(反向传播)

4.0神经网络反向传播