编程作业3.2：前馈神经网络
题目
- 上周使用了多类logistic回归，然而logistic回归不能形成更复杂的假设，因为它只是一个线性分类器。
- 在本次练习中，将使用前馈神经网络来识别手写数字(从0到9)。数据依然是MNIST手写体数据集，这里包含了5000个训练样本。
- 之前用了逻辑回归进行多元分类，这次用前馈神经网络进行预测。神经网络可以实现非常复杂的非线性的模型。我们将利用已经训练好了的权重进行预测。
编程实现
- 首先选择网络框架，这里作业中给出了框架，即包含输入层、隐藏层和输出层的3层框架。
- 由于x的维度是5000乘400，即有400个特征，因此输入层的神经元数量为400（不包含偏置单元，即常数项1），隐藏层的神经元数量作业中给出为25（不包含偏置单元），输出层的神经元数量由分类的类数所决定，因此是10。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
def load_weight(path):
data = loadmat(path)
return data['Theta1'], data['Theta2']
theta1, theta2 = load_weight('D:\BaiduNetdiskDownload\data_sets\ex3weights.mat')
theta1.shape, theta2.shape
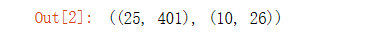
def load_data(path):
data = loadmat(path)
X = data['X']
y = data['y']
return X,y
X, y = load_data('D:\BaiduNetdiskDownload\data_sets\ex3data1.mat')
y = y.flatten() # 这里消除了一个维度，方便后面的计算 （5000，）
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # 为X添加了一列常数项 1，(5000, 401)
X.shape, y.shape
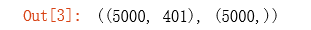
a1 = X
z2 = a1 @ theta1.T
z2.shape
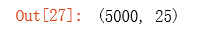
def sigmoid(z):
return 1 / (1 + np.exp(-z))
a2 = sigmoid(z2)
a2.shape
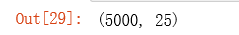
a2 = np.insert(a2, 0, 1, axis=1) # 为a2 添加了一列常数项1（偏置单元），(5000, 26)
a2.shape
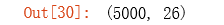
z3 = a2 @ theta2.T
a3 = sigmoid(z3)
a3.shape
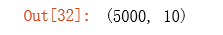
# np.argmax返回array中数值最大数的下标，默认将输入array视作一维，出现相同的最大，返回第一次出现的。
y_pred = np.argmax(a3, axis=1) + 1 # np.argmax(a, axis=None, out=None),a—-输入array,axis—-为0代表列方向，为1代表行方向,out—-结果写到这个array里面。y_pred.shape (5000,)
accuracy = np.mean(y_pred == y)
print ('accuracy = {0}%'.format(accuracy * 100)) # accuracy = 97.52%
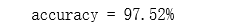
前馈函数时大概流程：
总结
- 在解决非线性假设问题中，当特征很多时如果还是利用logistic回归，那多项式的特征数目将会以初始特征数目的指数级速度产生，这样会造成算法运算量过大，甚至过拟合。
- 神经网络在解决非线性假设问题特征数很大的情况下一种非常好的算法。在数学上已经证明，只需一个包含足够多神经元的隐层，多层前馈网络就可以以任意精度逼近任意复杂度的连续函数。因此可以看书神经网络之强大。
- 类似于神经元细胞体，通过类似于树突的输入通道传递给神经元信息让它工作，再通过类似于轴突的输出通道输出结果。
- h在这里称为激活函数（activation function）（指代非线性函数\(g(z)=\frac{1}{1+e^{-z}}\)的另一个术语）
- 称逻辑单元（logistic unit）是一个带激活函数的人工神经元（artificial neuron）。
- 在激活函数中的参数又叫模型的权重。
- 第一层叫输入层（input layer），在这一层输入特征；最后一层叫输出层（output layer）输出最后的结果；中间层叫隐层（hidden layer）看不到输入或者输出的值。
- 此外有时还可以设置一个值为1的偏置单元（bias unit）。
