编程作业1.2:多变量线性回归
题目:
在本部分的练习中,需要预测房价,输入变量有两个特征,一是房子的面积,二是房子卧室的数量;输出变量是房子的价格。
编程实现:
X表示特征变量(面积、卧室数量)矩阵,y表示利润,一共47行数据。
编程语言:python 3.7.3
环境:jupyter notebook
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'D:\BaiduNetdiskDownload\data_sets\ex1data2.txt'
data2 = pd.read_csv(path, names=['Size', 'Bedrooms', 'Price'])
data2.head()
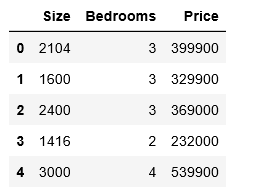
因为这两个特征的范围相差比较大,对于此任务,我们添加了另一个步骤特征缩放。
特征缩放:因为对于大多数的机器学习算法和优化算法来说,将特征值缩放到相同区间可以使得获取性能更好的模型。就梯度下降算法而言,例如有两个不同的特征,第一个特征的取值范围为1-10,第二个特征的取值范围为1-10000。在梯度下降算法中,代价函数为最小平方误差函数,所以在使用梯度下降算法的时候,算法会明显的偏向于第二个特征,因为它的取值范围更大,而且会导致多元梯度下降法收敛速度过慢。
- 常用的特征缩放算法有两种:
- 归一化(normalization):归一化算法是通过特征的最大最小值将特征缩放到[0,1]区间范围内;
\[x^{(i)}_{norm}=\frac{x^{(i)}-\mu}{x_{max}-x_{min}}
\]
- 标准化(standardization):对于许多机器学习算法来说,标准化也许会更好,标准化是通过特征的平均值和标准差将特征缩放成一个标准的正态分布,均值为0,方差为1。(经过处理的数据服从\(N(0,1)\),这在一定程度上改变了特征的分布)
\[x^{(i)}_{std}=\frac{x^{(i)}-\mu}{\sigma}
\]
这里采用特征归一化的方法,这个对于pandas来说很简单:
# mean() 函数用来取均值;std() 函数用来计算标准差
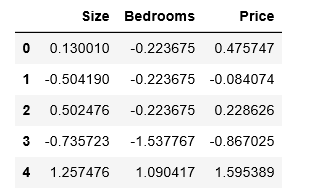
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
# 创建代价函数 J(θ)
# 传入的X,y,t_theta都是列向量
# X 中的每行为x1,x2,x3.....
def compute_cost(X,y,theta):
#print(t_theta.shape)
inner = np.power(((X.dot(theta.T))-y),2) # 后面的2表示2次幂
return sum(inner)/(2*len(X))
# add ones column
data2.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.array([0,0,0]).reshape(1,3)
# 输出矩阵 X2(训练集)、y2(目标变量)、theta2的维数验证是否正确
print(X2.shape)
print(y2.shape)
print(theta2.shape)
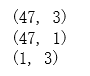
# 计算初始代价函数的值 (theta初始值为0)
compute_cost(X2, y2, theta2)

定义梯度下降函数,和编程作业1.1中相同,
# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, epoch=1000):
'''return theta, cost'''
temp = np.array(np.zeros(theta.shape)) # 初始化一个 theta 临时矩阵
parameters = int(theta.flatten().shape[0]) # 参数 theta 的数量
cost = np.zeros(epoch) # 初始化一个 ndarray ,包含每次迭代后的 cost 值
m = X.shape[0] # 样本数量 m
for i in range(epoch):
# 利用向量化同步计算 theta 值
# 注意 theta 是一个行向量
temp = theta - (alpha/m) * (X.dot(theta.T)- y).T.dot(X) # 得出一个theta行向量
theta = temp
cost[i] = compute_cost(X, y, theta) # 这个函数中,theta是变量,X,y是已知量
return theta,cost # 迭代结束之后返回 theta 和 cost 值
初始化学习速率α和要执行的迭代次数。
alpha = 0.01
epoch = 2000
运行梯度下降算法,得出 theta 和 cost :
final_theta, cost2 = gradientDescent(X2, y2, theta2, alpha, epoch)
计算梯度下降之后的代价函数的值:
compute_cost(X2, y2, final_theta)
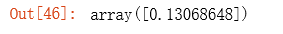
查看这一个的训练进程:
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(np.arange(epoch), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
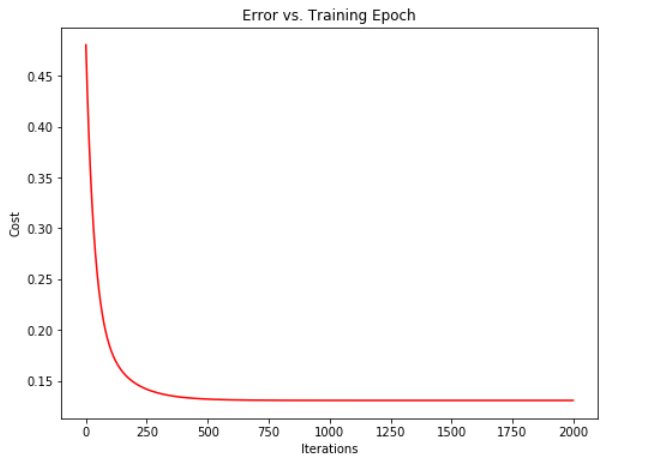
可以由图像观察得出梯度下降算法运行正确, cost 值不断收敛。
总结:
多变量线性回归的不能在二维图中绘制线性模型和数据,因此不能够直接的看出最终的拟合效果,所以画出梯度下降算法的迭代次数与代价函数的值的图像非常重要,通过这个图可以看出我们选择的学习效率α的值是否合适,以及梯度下降算法是否正常工作。
有之前单变量线性回归的基础之后,这次的编程作业好像轻松了不少,不过还在努力理解中,加油呀。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号