编程作业1.1:单变量线性回归
题目:
在本部分的练习中,您将使用一个变量实现线性回归,以预测食品卡车的利润。假设你是一家餐馆的首席执行官,正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车,而且你有来自城市的利润和人口数据。您希望使用这些数据来帮助您选择将哪个城市扩展到下一个城市。
编程实现
x表示人口数据,y表示利润,一共97行数据。
编程语言:python 3.7.3
环境:jupyter notebook
# NumPy 函数库是它是处理数值计算最为基础的类库,可以用来存储和处理大型多维矩阵
# pandas 提供了大量能使我们快速便捷地处理数据的函数和方法
# Matplotlib 是可视化工具,是 Python 的绘图库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 导入数据
path = 'D:\BaiduNetdiskDownload\data_sets\ex1data1.txt'
# pd.read_csv 将 TXT 文件读入并转化为数据框形式
# names 添加列名
# header 用指定的行来作为标题(表头),若原来无标题则设为 none
# 用到 Pandas 里面的 head( ) 函数读取数据(只能读取前五行)
data = pd.read_csv(path,header=None,names=['Population','Profit'])
data.head()
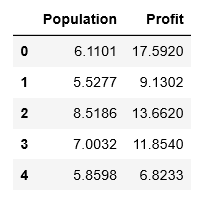
# 输出一些数据的统计量
data.describe()

在开始任何任务之前,通过可视化来理解数据通常是有用的。
对于这个数据集可以使用散点图来可视化数据,因为它只有两个属性(人口和利润)。
(在现实生活中遇到的许多其他问题都是多维度的,不能在二维图上画出来)
# 数值使用 matplotlib 软件包的 pyplot 子模块的 plot() 函数绘制
# 图形由show()函数体现
data.plot(kind='scatter', x='Population', y='Profit', figsize=(8,5))
plt.show(1)
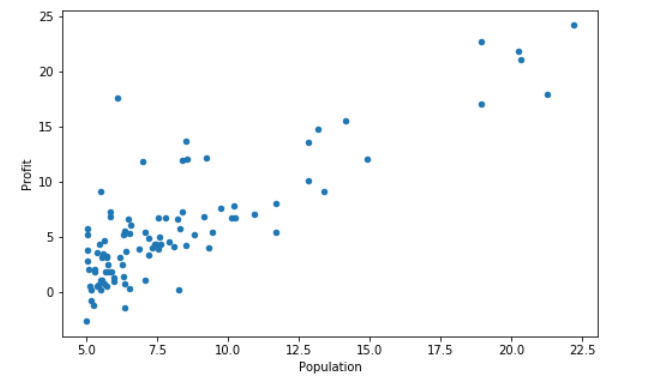
现在使用梯度下降来实现线性回归,以最小化成本函数。
首先,我们将创建一个以参数θ为特征函数的代价函数:
其中:
当然,在该题情况中Hypothesis为:
注意:式子中的 θ 是列向量,而程序中的 θ 是行向量,注意表达式的不同。
# 创建代价函数 J(θ)
# 传入的X,y,t_theta都是列向量
# X 中的每行为x1,x2,x3.....
def compute_cost(X,y,theta):
#print(t_theta.shape)
inner = np.power(((X.dot(theta.T))-y),2) # 后面的2表示2次幂
return sum(inner)/(2*len(X))
# 在训练集中插入一列1(其实是x0=1),方便我们可以使用向量化的解决方案来计算代价和梯度。
data.insert(0, 'Ones', 1)
# set X(training set), y(target variable)
# 设置训练集X,和目标变量y的值
cols = data.shape[1] # 获取列数
X = data.iloc[:,0:cols-1] # 输入向量X为前cols-1列
y = data.iloc[:,cols-1:cols] # 目标变量y为最后一列
# 代价函数是应该是 numpy 矩阵,所以我们需要转换X和Y,然后才能使用它们。 我们还需要初始化 theta 。
X = np.array(X.values)
y = np.array(y.values)
theta = np.array([0,0]).reshape(1,2) # 初始化向量θ为1*2维零矩阵
# 输出矩阵 theta、X(训练集)、y(目标变量)的维数验证是否正确
print(theta.shape)
print(X.shape)
print(y.shape)
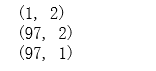
注意:这里使用矩阵array而不是matix。两个矩阵相乘,得用方法.dot()
# 计算初始代价函数的值 (theta初始值为0)
compute_cost(X, y, theta)
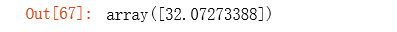
gradient descent(梯度下降算法)
使用向量化(vectorization)可以同时更新所有的 θ,可以大大提高效率
# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, epoch=1000):
'''return theta, cost'''
temp = np.array(np.zeros(theta.shape)) # 初始化一个 theta 临时矩阵
parameters = int(theta.flatten().shape[0]) # 参数 theta 的数量
cost = np.zeros(epoch) # 初始化一个 ndarray ,包含每次迭代后的 cost 值
m = X.shape[0] # 样本数量 m
for i in range(epoch):
# 利用向量化同步计算 theta 值
# 注意 theta 是一个行向量
temp = theta - (alpha/m) * (X.dot(theta.T)- y).T.dot(X) # 得出一个theta行向量
theta = temp
cost[i] = compute_cost(X, y, theta) # 这个函数中,theta是变量,X,y是已知量
return theta,cost # 迭代结束之后返回 theta 和 cost 值
初始化学习速率α和要执行的迭代次数。
alpha = 0.01
epoch = 2000
运行梯度下降算法,得出 theta 和 cost :
final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
我们可以使用我们拟合的参数计算训练模型的代价函数(误差)。
compute_cost(X, y, final_theta)
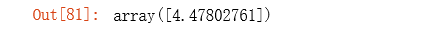
population = np.linspace(data.Population.min(), data.Population.max(), 97)
population.shape
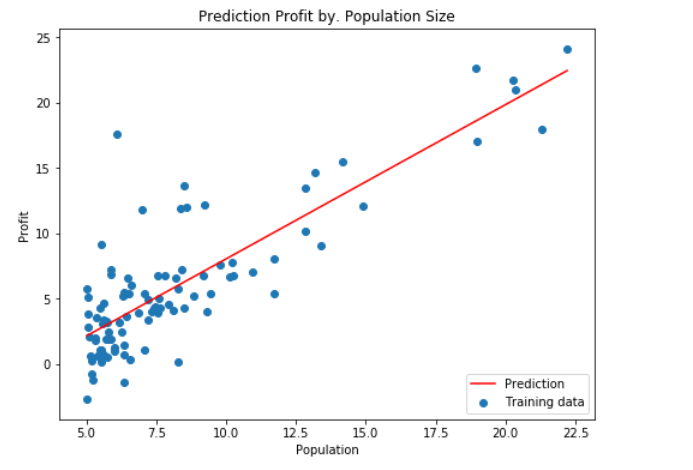
绘制线性模型以及数据,直观地看出它的拟合。
np.linspace()在指定的间隔内返回均匀间隔的数字。
population = np.linspace(data.Population.min(), data.Population.max(), 100) # 横坐标
profit = final_theta[0,0] + (final_theta[0,1] * population) # 纵坐标,利润
fig, ax = plt.subplots(figsize=(8, 6)) # 创建一个 8 * 6 点(point)子图
ax.plot(population, profit, 'r', label='Prediction')
ax.scatter(data['Population'], data['Profit'], label='Training data')
ax.legend(loc=4) # 4表示标签在右下角
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Prediction Profit by. Population Size')
plt.show()
由于梯度下降过程中每一次迭代都会得到一个cost值,下面我们根据cost的值来绘制图像。我们通常使用绘制cost图像的方式来观测梯度下降算法是否正常的运行,若是算法运行正常,该图像会一直下降。
fig, ax = plt.subplots(figsize=(8, 6)) # 创建一个 8 * 6 点(point)子图
ax.plot(np.arange(epoch), cost, 'r')
ax.set_xlabel('No. of Iteration')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Traning Epoch')
plt.show()
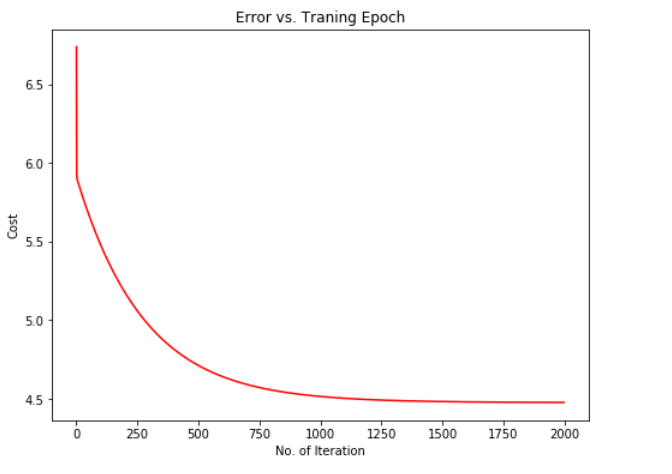
可以由图像观察得出梯度下降算法运行正确, cost 值不断收敛。
总结
对Python语言不太熟练导致这个作业做了很久很久,一直在查这个函数是什么,那个函数是什么。对jupyter notebook也差不多算是初次使用,一直在百度,这时候发现网络真的好神奇,什么问题一搜基本上都可以解决,还有对Markdown的公式编辑也弄了好久,之前没怎么用过公式这方面。但是最后看到运行结果还是很开心的,弄明白为什么之后更开心啦。这篇作业算是跟着网络上的教程一点一点学的,由于各种新手导致我一直在被动思考为什么要这样做而不是思考怎样做,之后要多多加油,争取有一天可以自己写代码。
参考资料
https://cloud.tencent.com/developer/news/323834
https://blog.csdn.net/Cowry5/article/details/80174130


 浙公网安备 33010602011771号
浙公网安备 33010602011771号