公钥密码

1. 公钥密码

　　公钥加密，私钥解密。

 

2. 密钥配送问题

　　对称密码中通信双方使用的密码是相同的，就引入了密钥配送问题。

　　解决密钥配送的方法：

　　　　通过事先共享密钥的方法来解决。特点是局限性很大，通信双方都存放大量的密钥。

　　　　通过密钥分配中心解决。特点是中心需要共享每个人的密钥，中心的安全性要求很高，负荷会非常大。

　　　　通过Diffie-Hellman来解决。即使被窃听，也不会产生问题。

　　　　通过公钥密码解决。加密密钥和解密密钥分开的思路。

 

3. 公钥密码的特点

　　加密密钥，公钥，是公开的。

　　解密秘钥，私钥，不是公开的。

　　公钥和私钥一一对应，一个公钥和一个私钥统称密钥对，而且公钥和私钥不能单独生成。

　　密钥分加密密钥和解密秘钥；发送者只需加密密钥，接收者只需解密密钥；要求解密秘钥不能被窃听者获取，加密密钥被窃听者获取信息也不会泄露。

　　公钥密码的运算速度很慢，只有对称密码的几百分之一。

　　公钥密码不能解决公钥合法性的问题，这个问题被称为公钥认证问题。

 

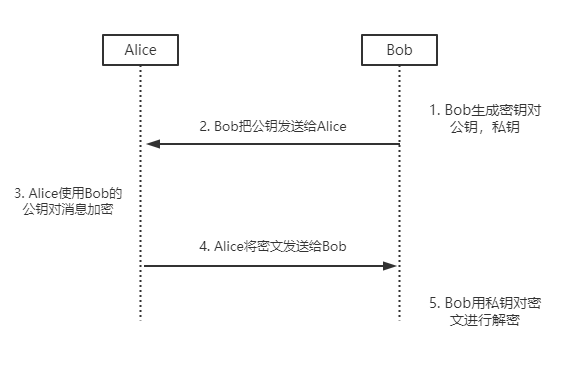
4. 公钥密码简要的通信流程

　　

 

5. 时钟运算

　　为了很好的理解RSA算法，需要了解时钟运算相关的数学原理。

 　　加法：

　　　　时钟加法是一个除法求余运算，即mod，取模运算。例如7加上20，对应的时钟运算是 （7+20）/ 12 = 27 / 12 = 2余3

　　减法：

　　　　加法的逆运算。例如（7 + A）mod 12 = 0，统计（ X+Y）mod 12 = 0 的情况，查表可得到一些数字之间的联系。

　　乘法：

　　　　先进行乘法运算，再进行除法求余运算。7 x 4 转为 7 x 4 mod 12 = 4

　　除法：

　　　　7 x A mod 12 = 1，简化为在mod12 的条件下存在倒数的数，它们和12的公约数都只有1。

　　　　是否存在倒数，可以通过这个数和12的最大公约数是否为1，这个条件来判断。也就是和12互质的数。

　　　　时钟除法不一定有解，时钟运算中“某个数是否存在倒数”与RSA中“一个公钥是否存在相应的私钥”，两个问题直接相关。

　　乘方：

　　　　进行算术乘方，再对结果进行mod运算，计算过程中可以在中间步骤求mod，避免过多的运算。

　　对数：

　　　　算术运算中对数不难求解。时钟运算中的对数称为离散对数。当数字很大时，求离散对数十分困难。

　　　　目前还未发现快速解决离散对数的算法。Diffie-Hellman密钥交换协议以及ElGamal公钥算法中就运用了离散对数。

 

6. RSA

　　什么是RSA

　　　　应用最广泛的公钥密码算法，由三位发明者Ron Rivest，Adi Shamir和Leonard Adleman的姓氏首字母组成。

　　RSA中明文，密文和密钥都是数字，运算都是大数运算。

　　RSA加密

　　　　明文^E mod N = 密文　　明文做E次方乘方运算，再对N求mod。

　　　　E和N的组合就是公钥。

　　RSA解密

　　　　密文^D mod N = 明文　　密文做D次方乘方运算，再对N求mod。

　　　　D和N的组合就是私钥。

　　生成密钥对

　　　　E，D，N三个数就可以生成密钥对。

　　　　步骤：

　　　　　　求N：准备两个足够大的质数p和q，N = p x q。

　　　　　　求L：L是p-1和q-1的最小公倍数，L = lcm(p-1, q-1)

　　　　　　求E：1<E<L，E和L最大公约数必须是1（互质），gcd（E，L） = 1。

　　　　　　求D：1<D<L，E x D mod L = 1，要保证有满足条件的D，就要保证E和L最大公约数是1。

　　　　其中：p，q和E都是使用伪随机数生成器生成。

 

7.  对RSA的攻击

　　由于公钥是公开的，破译者知道E和N。不知道生成密钥对过程中的p，q和L。

　　通过密文求明文：大数的离散对数问题，求解复杂。

　　暴力破解求D：逐一尝试可以作为D的数字破译RSA，难度随D的长度增大而变难。

　　　　　　　　   RSA中p和q长度在1024比特以上，N为2048比特以上，破解D需要在2048比特上破解，及其困难。

　　通过E和N求出D：D是由E算出来的，E x D mod L = 1；L由p和q算出来，破译者不知道p和q，p和q交出去相当于交出了私钥。

　　　　　　　　　　 对N进行质数分解，一旦发现了大数进行质数分解的高效算法，RSA就能被破译。

　　　　　　　　　    推测p和q进行攻击，p和q是由伪随机数生成器生成的，伪随机数生成器算法较弱可能被破译者推测出来p和q。

　　　　　　　　　　 数学角度证明了“对N进行质因数分解”与“求D”在确定性多项式时间内是等价的。

　　中间人攻击：虽不能破解RSA，但确是对机密性的一种有效攻击。

　　　　　　　　Mallory窃听了Alice和Bob的通话后，冒充Bob发送了自己公钥，并获取到Bob的公钥。Alice和Bob的通话被替换成了Alice和Mallory的通话。

　　　　　　　　解决中间人攻击的方法是数字证书。

　　选择密文攻击：发送任意数据，服务器都会认为是密文进行解密，并返回相应的解密错误信息，可以作为破译提示，使攻击者获得密钥和明文信息。

　　　　　　　　　解决选择密文攻击的方法是RSA-OAEP，最优非对称加密填充，对密文进行认证。

 

8. 其他公钥算法

　　ELGamal：利用了mod N下求离散对数的困难度。缺点是经加密的密文长度是明文的2倍。

　　Rabin：利用了mod N下求平方根的困难度。

　　椭圆曲线密码：ECC，特点是所需的密钥长度比RSA短。将椭圆曲线上的特定的点进行特殊的乘法运算，这种乘法运算的逆运算非常困难。

 

9. 补充

　　具备同等抵御暴力破解强度的密钥长度比较：

　　　　对称密码AES　　　　　　公钥密码RSA

　　　　　　　　 128　　　　　　　　　　3072

　　　　　　　　 192　　　　　　　　　　7680

　　　　　　　　 256　　　　　　　　　  15360

　　公钥密码的处理速度只有对称密码的几百分之一。

　　质数不会被用光，512比特可以容纳的质数数量大约是10的150次方。

　　RSA的私钥和对N进行质数分解是等价的。

　　RSA处理密码劣化的建议：

　　　　1024比特的RSA不应用于新的用途。

　　　　2048比特的RSA可在2030年前被用于新的用途。

　　　　4096比特的RSA可在2031年之后被用于新的用途。