浅谈TCN
一、 提出原因
-
对序列数据进行建模时,应将卷积网络作为首要选择。
-
卷积网络在许多任务中实现比RNN更好的性能。
-
避免梯度爆炸、梯度消失的问题。
-
并行运算可以提高性能。
-
参考源文献
-
二、 基础模型
TCN 是 Temporal Convolutional Network 的缩写,由具有相同输入和输出长度的扩张的因果 1D 卷积层组成。以下部分详细介绍了这些术语的实际含义。
1.1D Convolutional Network
一维卷积网络将一个 3 维张量作为输入,并输出一个 3 维张量。输入张量参数:(batch_size, input_length, input_size)
输出张量参数: (batch_size, input_length, output_size)。
由于 TCN 中的每一层都具有相同的输入和输出长度,因此只有输入和输出张量的第三维不同。在单变量情况下,input_size 和 output_size 都将等于 1。在更一般的多变量情况下,input_size 和 output_size 可能不同,因为我们可能不想预测输入序列的每个分量。
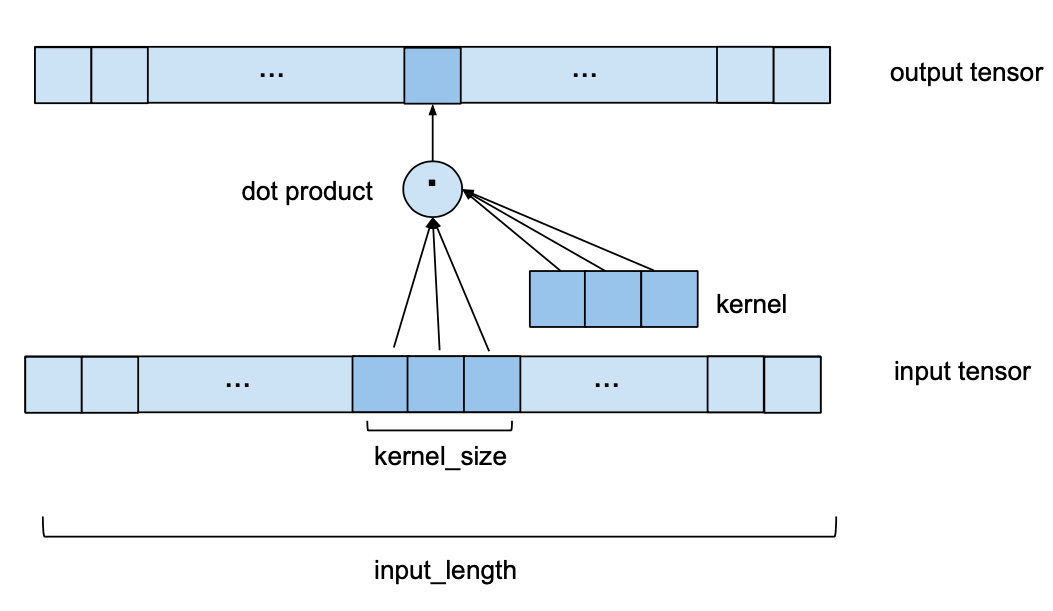
-
如上图所示,kernel_size:3。
-
将输入的子序列和相同长度的学习权重的kernel向量进行点乘。
-
输入序列的kernel_size窗口向右移动了一个元素(stride总是被设置为1)。
-
同一组kernal权重重复用于计算一个卷积层的每一个输出。
![]()
-
为了使视觉效果更简单,不再显示与内核向量的点乘,而是对同一个kernal size中每个元素间进行点乘。
-
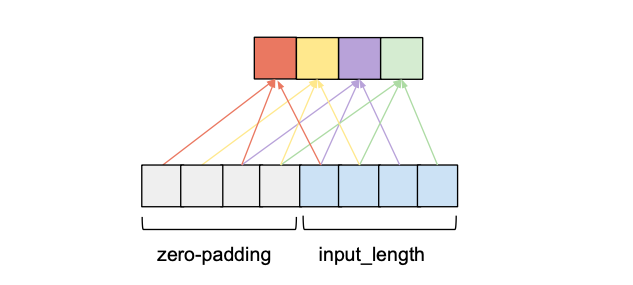
为了确保输出序列与输入序列具有相同的长度,应用了一些零填充。
2.因果卷积 Causal Convolution
对于卷积层的因果关系,
输入序列:{0, ..., input_length - 1}中的每一个i,输出序列的第i个元素只能依赖于输入序列中索引为{0, ..., i}的元素。
输出序列中的一个元素只能依赖于输入序列中排在它前面的元素。
如前所述,为了确保输出张量与输入张量具有相同的长度,我们需要应用零填充。如果我们只在输入张量的左边应用零填充,那么因果卷积就会得到保证。
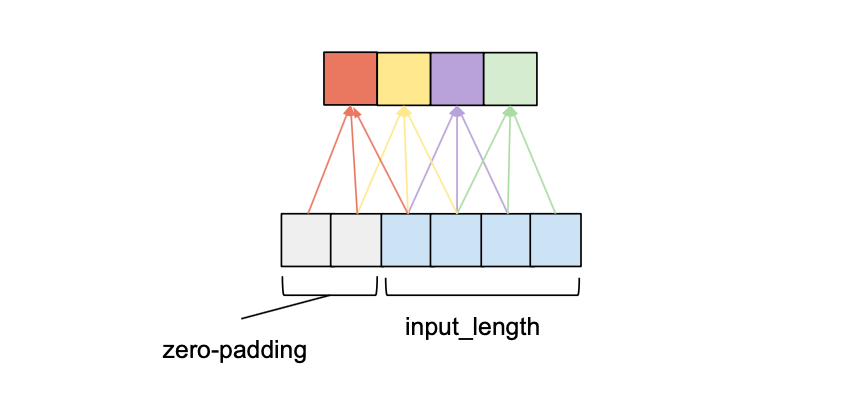
我们可以看到,通过 2 个条目的左零填充,我们可以在遵守因果关系规则的同时实现相同的输出长度。事实上,在没有膨胀的情况下,维持输入长度所需的零填充条目数= kernel_size – 1。
3.扩张 Dilation
预测模型的一个理想质量是,输出中某一特定条目的值取决于输入中所有先前的条目,即所有索引小于或等于它的条目。当接受域,即影响输出中特定条目的原始输入的条目集,具有输入_长度的大小时,就能实现这一点。我们也把这称为 "全历史覆盖(full history coverage)"。正如我们之前看到的,一个传统的卷积层使输出中的一个条目依赖于输入中索引小于或等于自己的kernel_size条目。
例如,如果我们的kernel_size是3,输出中的第5个元素将依赖于输入中的第3、4和5个元素。当我们把多层堆叠在一起时,这个范围会扩大。在下图中,我们可以看到,通过堆叠两个kernal-size为3的层,我们得到的感受野(receptive field)为5。
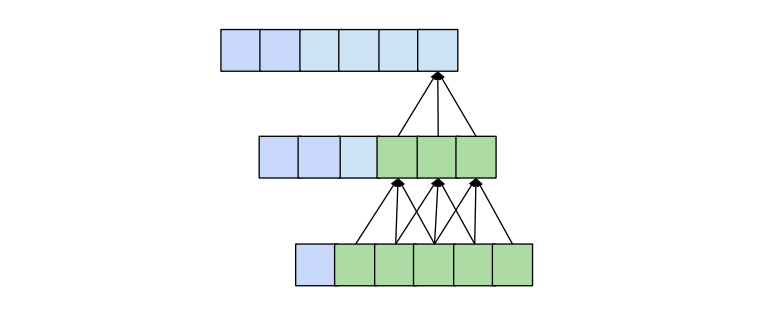
具有 n 层和 kernel_size的一维卷积网络具有的感受野(receptive field)r 为
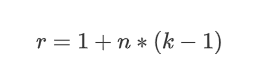
r = 1 + n*(k-1)
$$
为了求解全覆盖需要的层数,令r= l,并求解层数n
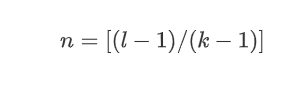
n = [(l-1)/(k-1)]
$$
上式解读:
这意味着,给定一个固定的内核大小,全历史覆盖所需的层数与输入张量的长度成线性关系,这将导致网络很快变得非常深,导致模型具有非常多的参数,需要更长的时间来训练。此外,高层数已被证明会导致与损失函数梯度有关的退化问题。因此在保持层数相对较少的情况下,增加感受野大小的一个方法是向卷积网络引入扩张。
扩张的定义:
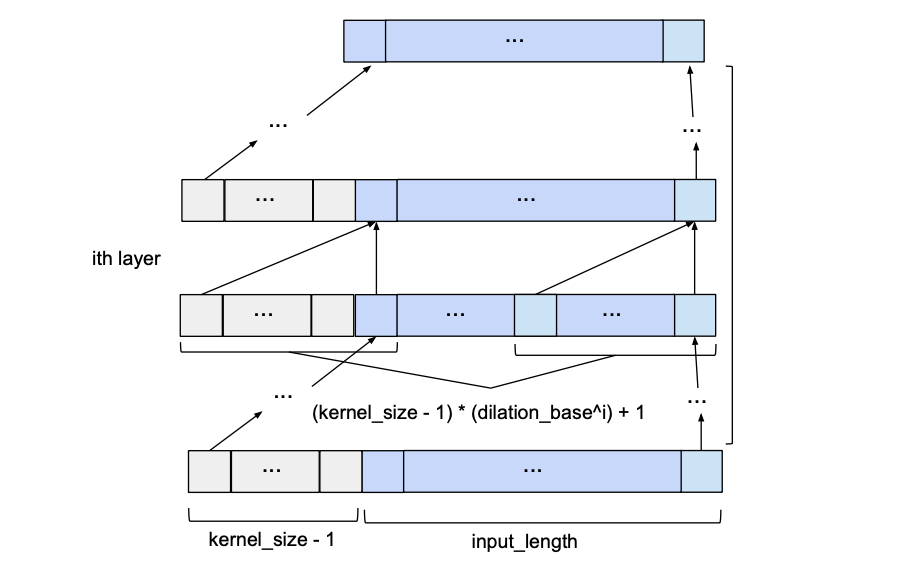
卷积层中的扩张是指用于计算输出序列中一个条目的输入序列元素之间的距离。因此,一个传统的卷积层可以被看作是一个1扩张的层,因为1个输出值的输入元素是相邻的。下图显示了一个2分层的例子,输入长度为4,核大小为3。
-
与 1-dilated 的情况相比,该层的感受野分布在 5 而不是 3 的长度上。更一般地,内核大小为 k 的 d-dilated 层的感受野分布在 1+d 的长度上*(k-1)。如果 d 是固定的,这仍然需要一个与输入张量长度呈线性关系的数字来实现完全的感受野覆盖(我们只是减小了常数)。
-
这个问题可以通过在各层向上移动时以指数形式增加d的值来解决。为此,我们选择了一个常数dilation_base的整数b,这将让我们计算特定层的dilation d与它下面的层数i的函数,即d=b*i。
下图显示了一个输入长度为10,内核大小为3,dilation_base=2 的网络,其结果是有3个扩张的卷积层来实现全覆盖。
![]()
4.TCN模型概述
考虑到输入长度、内核大小、扩张基数和全历史覆盖所需的最小层数,基本的TCN网络如上图所示。
考虑到这些观察,我们可以计算出我们的网络需要多少层n才能实现全历史覆盖。内核大小为k,扩张基数为b,其中k≥b,以及输入长度为l,以下不等式对于全历史覆盖必须成立。
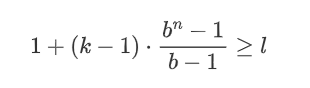
1+(k-1) \cdot \frac{b^{n}-1}{b-1} \geq l
$$
最小层数求解:
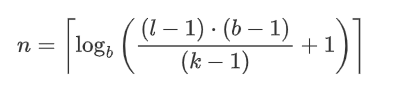
n=\left\lceil\log _{b}\left(\frac{(l-1) \cdot(b-1)}{(k-1)}+1\right)\right\rceil
$$
三、 TCN-预测
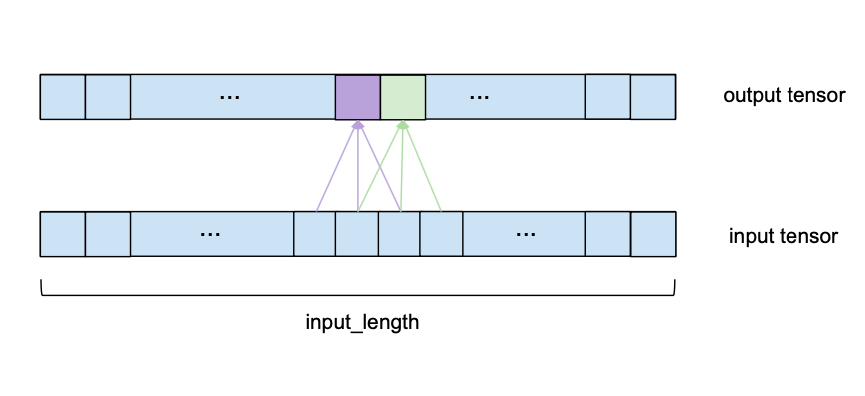
以上只谈到了 "输入序列 "和 "输出序列",而没有涉及到它们之间的关系。在预测的背景下,我们希望预测一个时间序列在未来的下一个条目。
为了训练我们的TCN网络进行预测,训练集将包括(输入序列(input series),目标序列(target series))输入序列——给定时间序列的同等大小的子序列对。目标序列——相对于其各自的输入序列向前移动了一定数量的output_length的序列。
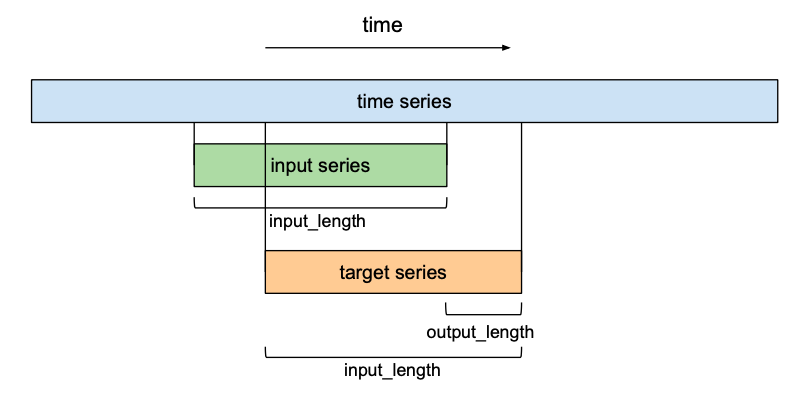
-
利用滑动窗口的方法可以从一个时间序列中创建许多重叠的输入和目标序列对。
-
。。。
四、模型的改善
1.残缺块 Residual Blocks
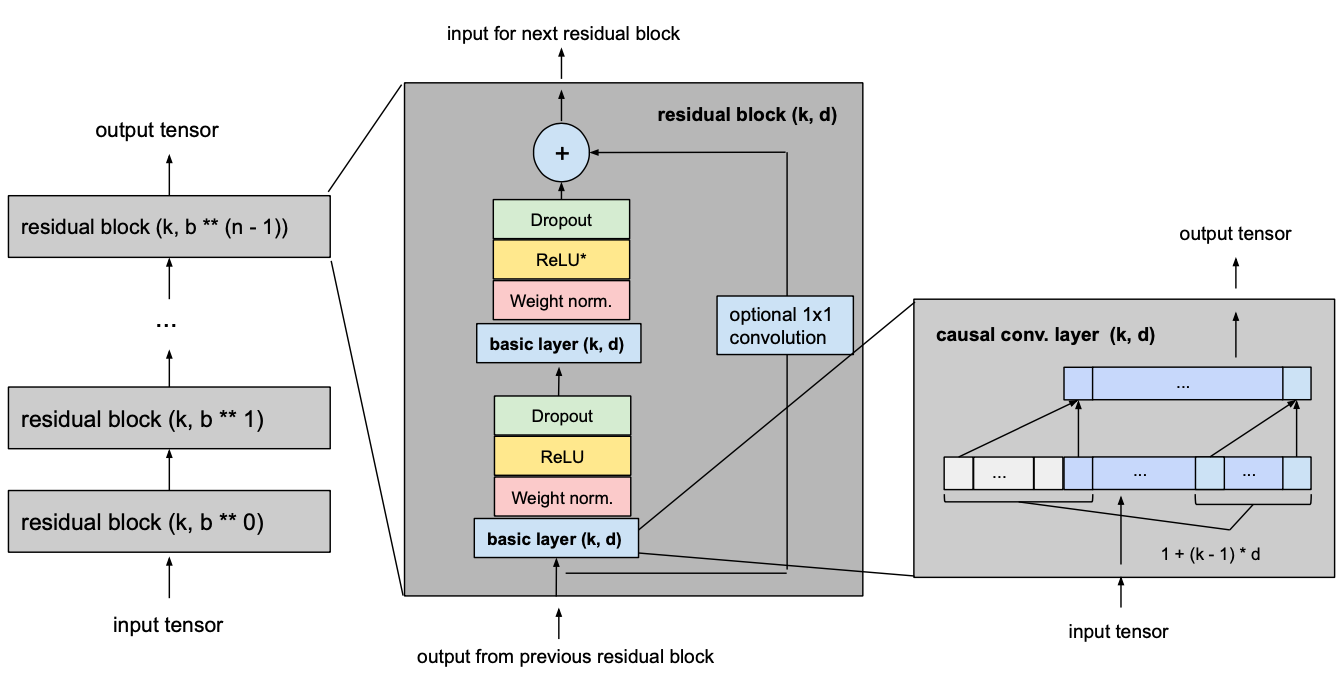
将模型的基本构件从简单的一维因果卷积层(图1)改为由2个具有相同扩张因子的层和一个剩余连接组成的剩余块(图2)。
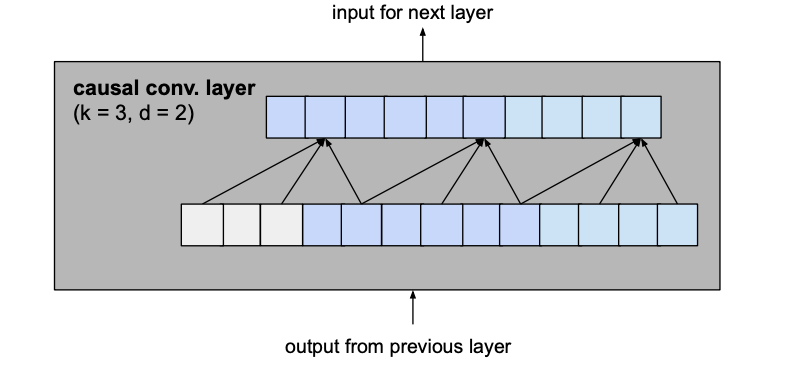
图一:因果卷积

图二:残缺块
这两个卷积层的输出将被添加到剩余块的输入中,以产生下一个块的输入。对于网络的所有内部块,即除了第一个和最后一个以外,输入和输出通道的宽度是相同的,即num_filters。由于第一个残差块的第一个卷积层和最后一个残差块的第二个卷积层可能有不同的输入和输出通道宽度,残差张量的宽度可能需要调整,这是用1×1卷积来完成的。
这一变化影响了全覆盖所需最小层数的计算。现在我们必须考虑有多少个剩余区块才能实现全接收场的覆盖。在一个TCN中添加一个残余块,比添加一个基本因果层时增加两倍的感受野宽度,因为它包括2个这样的层。因此,一个扩张基数为b、内核大小为k≥b、残余块数为n的TCN的接收场总大小r可以计算为
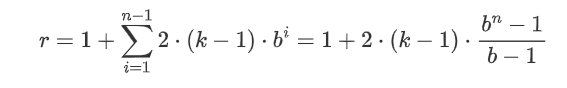
r=1+\sum_{i=1}^{n-1} 2 \cdot(k-1) \cdot b^{i}=1+2 \cdot(k-1) \cdot \frac{b^{n}-1}{b-1}
$$
最小层数求解:
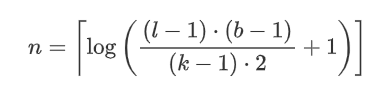
n=\left\lceil\log \left(\frac{(l-1) \cdot(b-1)}{(k-1) \cdot 2}+1\right)\right]
$$
2.激活、归一化、正则化
激活
为了使我们的TCN不仅仅是一个过于复杂的线性回归模型,需要在卷积层之上添加激活函数以引入非线性。ReLU激活被添加到两个卷积层之后的剩余块中。
归一化
为了对隐藏层的输入进行归一化(这可以抵消梯度爆炸等问题),将权重归一化应用于每个卷积层。
正则化
为了防止过拟合,在每个残差块的每个卷积层之后通过 dropout 引入正则化。下图显示了最终的残差块。
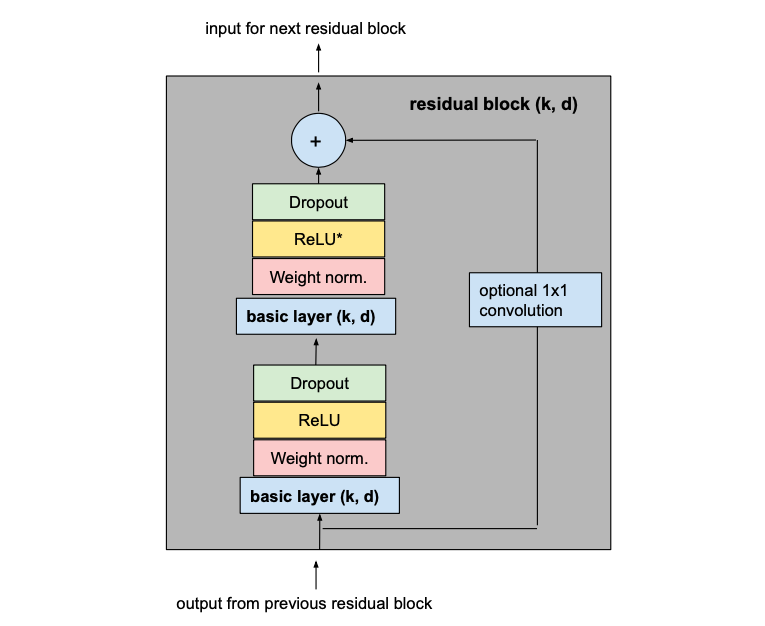
3.最终模型


 浙公网安备 33010602011771号
浙公网安备 33010602011771号