负载均衡算法WRR介绍
一、负载均衡
负载均衡是一个很大的概念,既有从硬件层面来解决问题的,又有从软件层面解决的,有关负载均衡的介绍,推荐阅读: http://os.51cto.com/art/201108/285359.htm,(11年的文章你会不会吐槽我不负责任)
本文主要介绍负载均衡算法中很简单的一种WRR(Weighted Round Robin),加权轮训调度算法,并且配合实现以及对它存在问题进行分析和提出一些优化策略。
二、原始的WRR算法
假设有3台机器a,b,c权重分别为5,1,1,原始的WRR算法实现是:每次选出权重最大的,给其权重减1,直到权重全部为0后,按照此时生成的序列轮训。
| 请求编号 | 选前权重值 | 被选中server | 选后权重值 |
|---|---|---|---|
| 1 | 5,1,1 | a | 4,1,1 |
| 2 | 4,1,1 | a | 3,1,1 |
| 3 | 3,1,1 | a | 2,1,1 |
| 4 | 2,1,1 | a | 1,1,1 |
| 5 | 1,1,1 | a | 0,1,1 |
| 6 | 0,1,1 | b | 0,0,1 |
| 7 | 0,0,1 | c | 0,0,0 |
算法很容易理解,最终确定的轮序序列是a,a,a,a,a,b,c,虽然此时负载是均衡的(5:1:1),但是前五次都去访问了a机器,b和c机器是空闲的,这样并不是最好的,理想状态是在均衡的情况下让访问次数也均衡开,于是就有了下面的SWRR(Smooth Weighted Round Robin),平滑加权轮训调度算法。
三、改进的SWRR算法
继续上面的例子,这次我们的策略是:
- 从权重中选出最大的,减去总权重
- 然后再给每个权重加上自身权重初始值
- 再次轮训,直到权重为0,确定序列
| 请求编号 | 选前权重值 | 被选中server | 选后权重值 |
|---|---|---|---|
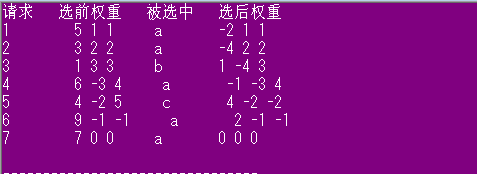
| 1 | 5,1,1 | a | -2,1,1 |
| 2 | 3,2,2 | a | -4,2,2 |
| 3 | 1,3,3 | b | 1,-4,3 |
| 4 | 6,-3,4 | a | -1,-3,4 |
| 5 | 4,-2,5 | c | 4,-2,-2 |
| 6 | 9,-1,-1 | a | 2,-1,-1 |
| 7 | 7,0,0 | a | 0,0,0 |
说明:
- 第一行最后的-2 , 1 , 1 是 5(当前权值最大) - 7(总权重)=-2 ,其他两个值不变得来的。
- 第二行的 3,2, 2, 是 上一行的 -2 , 1 , 1 加 各自权重初始值 5 ,1 1 得来的。(3=-2+5 , 2 = 1+1 , 2 = 1+1)
这样我们得到的最终轮训序列是 :a,a,b,a,c,a,a ,是不是效果比之前好多了,如丝般柔顺,实现也很简单(代码中去掉了输出代码):
while (flag) {
/*找到目前的最大元素*/
auto big = std::max_element(std::begin(temp),std::end(temp));
/*找出最大元素的下标*/
auto bigIndex = std::distance(std::begin(temp),big);
temp[bigIndex] -= TOTAL; //找出的最大元素减去总权重
/*各自加上初始权重*/
for(int j = 0; j < temp.size();++j) {
temp[j] += weight[j];
}
}
但是这个算法还是存在问题:在大量并发来临的那一刻,我们第一次始终会选择a机器,那它必然就会爆掉。
应对这样的问题:我们可以在生成序列之后随机选择一个开始,比如我们有5台负载的机器,它们都生成了
a,a,b,a,c,a,a的序列,但是我们不完全按照这个序列轮训,在每台机器上可以随机选择一个开始,那生成的序列就可能变成下面这样:
| 机器 | 序列 |
|---|---|
| 机器1 | a,b,a,c,a,a… |
| 机器2 | b,a,c,a,a,a,a… |
| 机器3 | a,a,b,a,c,a,a… |
| 机器4 | c,a,a,a,a,b,a… |
| 机器5 | a,b,a,c,a,a… |
这样能降低些第一台机器被爆掉的概率。
[完]



