深度学习-循环神经网络笔记
循环神经网络(Recurrent Neural Network, RNN)与递归神经网络(Recursive Neural Network, RNN)在简写上是一样的,本次笔记只针对循环神经网络,在此之前先说一下,针对这两个神经网络,有些博客只是从名字上将其分开来了,具体的也没详细介绍,经过大量的中文搜索,还是发现了有不少热心大神将它们认真的讲述了,本文暂推荐https://zybuluo.com/hanbingtao/note/541458这篇描述。本文的笔记大都转自这篇文章。
全连接神经网络和卷积神经网络他们都只能单独处理一个个的输入,前一个输入和后一个输入是完全没有关系的。但是,某些任务需要能够更好的处理序列的信息,即前面的输入和后面的输入是有关系的。比如,当我们在理解一句话意思时,孤立的理解这句话的每个词是不够的,我们需要处理这些词连接起来的整个序列;当我们处理视频的时候,我们也不能只单独的去分析每一帧,而要分析这些帧连接起来的整个序列。这时,就需要用到深度学习领域中另一类非常重要神经网络:循环神经网络(Recurrent Neural Network)。
下图是一个简单的循环神经网络如,它由输入层、一个隐藏层和一个输出层组成:
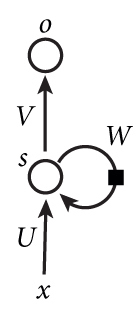
如果把上面有W的那个带箭头的圈去掉,它就变成了最普通的全连接神经网络。x是一个向量,它表示输入层的值(这里面没有画出来表示神经元节点的圆圈);s是一个向量,它表示隐藏层的值(这里隐藏层面画了一个节点,你也可以想象这一层其实是多个节点,节点数与向量s的维度相同);U是输入层到隐藏层的权重矩阵;o也是一个向量,它表示输出层的值;V是隐藏层到输出层的权重矩阵。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。
如果把上面的图展开,循环神经网络也可以画成下面这个样子:
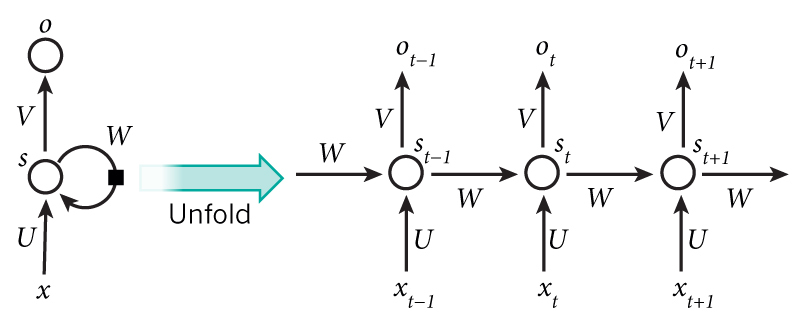
这个网络在t时刻接收到输入xt之后,隐藏层的值是st,输出值是ot。关键一点是,st的值不仅仅取决于xt,还取决于st-1。我们可以用下面的公式来表示循环神经网络的计算方法:
![]()
式1是输出层的计算公式,输出层是一个全连接层,也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵,g是激活函数。式2是隐藏层的计算公式,它是循环层。U是输入x的权重矩阵,W是上一次的值st-1作为这一次的输入的权重矩阵,f是激活函数。
我们可以把st-1一直向前循环可以得到:
![]()
输出值ot是关于st的表达式,它是受前面历次输入值xt-1,xt-2,xt-3,...影响的,这就是为什么循环神经网络可以往前看任意多个输入值的原因。
双向循环神经网络
双向循环网络如图:
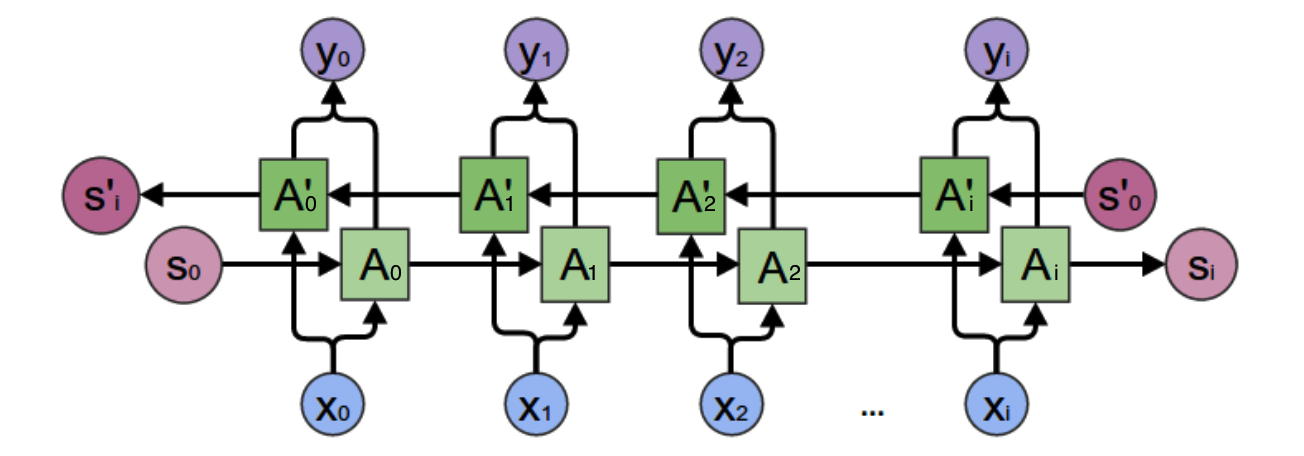
先考虑图中的y2的计算,从上图可以看出,双向卷积神经网络的隐藏层要保存两个值,一个A参与正向计算,另一个值A'参与反向计算。最终的输出值y2取决于A2和A'2,可以如下计算:
![]()
![]()
可以看出一般的规律:正向计算时,隐藏层的值st与st-1有关;反向计算时,隐藏层的值s't与s't-1有关;最终的输出取决于正向和反向计算的加和。仿照式1和式2,写出双向循环神经网络的计算方法:
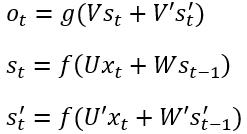
从上面三个公式我们可以看到,正向计算和反向计算不共享权重,也就是说U和U'、W和W'、V和V'都是不同的权重矩阵。
深度循环神经网络
前面介绍的循环神经网络只有一个隐藏层,当然也可以堆叠两个以上的隐藏层,这样就得到了深度循环神经网络。如下图所示:
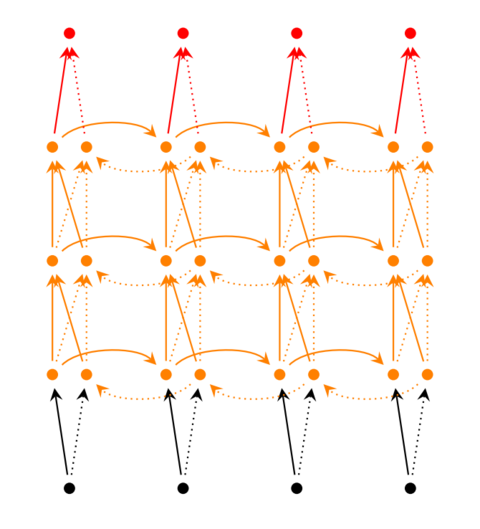
循环神经网络的训练
循环神经网络的训练算法:BPTT
BPTT算法是针对循环层的训练算法,它的基本原理和BP算法是一样的,也包含同样的三个步骤:
- 前向计算每个神经元的输出值;
- 反向计算每个神经元的误差项δj值,它是误差函数E对神经元j的加权输入netj的偏导数;
- 计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。由于https://zybuluo.com/hanbingtao/note/541458这篇运用了数值计算里面的矩阵运算方法,时间长了有点遗忘了,经过多番搜寻找到了https://www.jianshu.com/p/87aa03352eb9这篇比较容易理解的数学表达。循环层如下图所示:
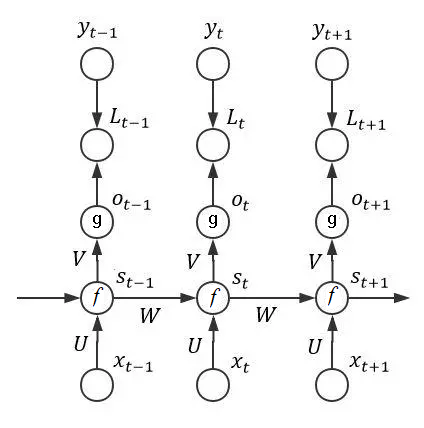
上图表明了RNN网络的完整拓扑结构,从图中我们可以看到RNN网络中的参数情况。在这里我们只分析t时刻网络的行为与数学推导。t时刻网络迎来一个输入xt,网络此时刻的神经元状态st用如下式子表达:
![]()
为了方便做了如下变换:
![]()
RNN的损失函数选用交叉熵(Cross Entropy),这是机器学习中使用最广泛的损失函数之一了,其通常的表达式如下所示:
![]()
![]()
需要说明的是:yt是t时刻输入的真实标签值,ot为模型的预测值,N代表全部N个时刻。下文中为了书写方便,将Loss简记为L。在结束本小节之前,最后补充一个softmax函数的求导公式:
BPTT算法
由于RNN模型与时间序列有关,因此不能直接使用BP(back propagation)算法。针对RNN问题的特殊情况,提出了BPTT算法。BPTT的全称是“随时间变化的反向传播算法”(back propagation through time)。这个方法的基础仍然是常规的链式求导法则,接下来开始具体推导。虽然RNN的全局损失是与全部N个时刻有关的,但为了简单笔者在推导时只关注t时刻的损失函数。
首先求出t时刻下损失函数关于ot*的微分:
![]()
求出损失函数关于参数V的微分:
因此,全局损失关于参数V的微分为:
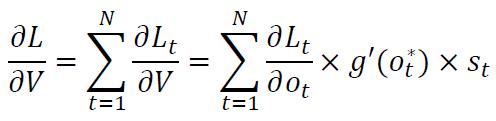
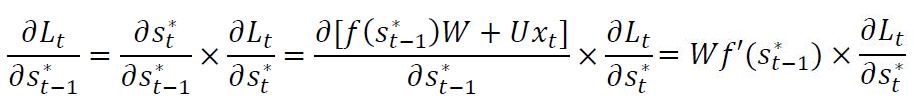
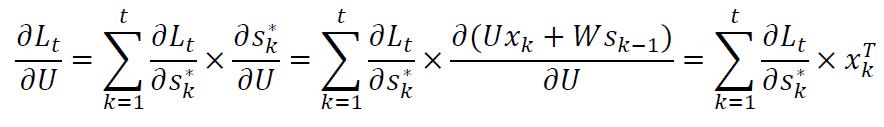
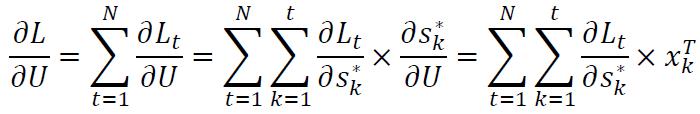
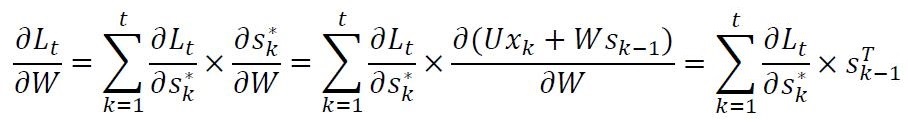
因此,全局损失关于参数W的微分结果为:
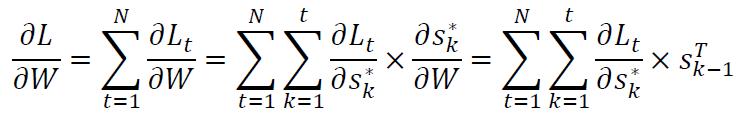
至此,全局损失函数关于三个主要参数的微分都已经得到了。整理如下:

接下来进一步化简上述微分表达式,化简的主要方向为t时刻的损失函数关于ot的微分以及关于st*的微分。已知t时刻损失函数的表达式,求关于ot的微分:
![]()
softmax函数求导:
![]()
因此:
![]()
又因为:
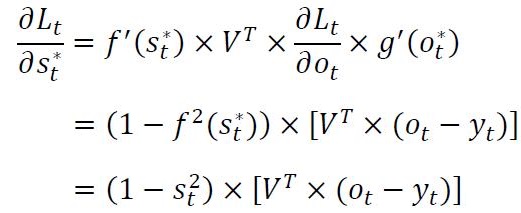
且:
![]()
有了上面的数学推导,我们可以得到全局损失关于U,V,W三个参数的梯度公式:
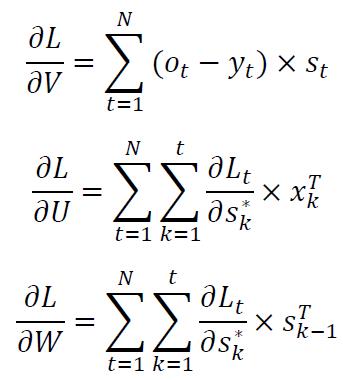
由于参数U和W的微分公式不仅仅与t时刻有关,还与前面的t-1个时刻都有关,因此无法写出直接的计算公式。不过上面已经给出了t时刻的损失函数关于st-1的微分递推公式,想来求解这个式子也是十分简单的,在这里就不赘述了。
以上就是关于BPTT算法的全部数学推导。从最终结果可以看出三个公式的偏微分结果非常简单,在具体的优化过程中可以直接带入进行计算。对于这种优化问题来说,最常用的方法就是梯度下降法。针对本文涉及的RNN问题,可以构造出三个参数的梯度更新公式: